Лавров Михаил Анатольевич : другие произведения.

Электромагнетизм

Самиздат: [Регистрация] [Найти] [Рейтинги] [Обсуждения] [Новинки] [Обзоры] [Помощь|Техвопросы]
Ссылки:
Школа кожевенного мастерства: сумки, ремни своими руками
Оценка: 8.00*5  Ваша оценка:
  • Аннотация:
    на правах мнения

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНТИПОДНОЙ ЭКВИВАЛЕНТНОСТИ
ФИЗИКИ ЭЛЕКТРОМАГНЕТИЗМА И ГРАВИТАЦИИ
Извлечение из "ТЕОРИИ КВАДРАТА"
Тема статьи: Э Л Е К Т Р О М А Г Н Е Т И З М
А Н Н О Т А Ц И Я

Уважаемый Читатель в случае возникновения у Вас вопросов после ознакомления со статьёй вы можете связаться с автором по электронной почте: misha.ml42@mail.ru

Изучение любого природного явления предопределяет двойственный характер. С одной стороны, когда сторонний наблюдатель впервые встречается с тем или иным природным явлением, в первую очередь он изучает его внешние признаки. В этом случае он выступает представителем следственной стороны и всё изучение явления носит описательный характер.
По мере же накопления сведений об изучаемом явлении, возникает необходимость раскрыть природную суть явления, его причинную сторону. Когда это удаётся, то исследователь из (образно) лагеря следствия как бы перемещается в лагерь причины.
В отношении электромагнетизма, несмотря на большой временной промежуток с момента изучения данного явления − с 1820 года, когда датский физик Г.Х. Эрстед впервые приступил к изучению действия магнитного поля прямолинейного тока на магнитную стрелку, можно констатировать, что до сих пор объяснение различных опытов по электромагнетизму носит следственный характер. Чтобы убедиться в этом, достаточно обратиться к любому современному учебнику по физике. В них объяснение подобных опытов проводится с позиции искусственных правил − правило левой или правой рук, а также правила буравчика.
В то же время, на сегодняшний момент времени доподлинно известно, что воздействие электрического и магнитного полей на электрически заряженные или намагниченные тела осуществляется посредством электромагнитных квантов или фотонов. Но о том, как подобные действия осуществляются на практике, необходимые сведения в учебниках по физике отсутствуют.
В предлагаемой Читателю статье излагается методика антиподно − эквивалентного подхода к объяснению механизма действия электрического и магнитного полей на электрически заряженные и намагниченные тела, с позиции действия на них квантов электромагнитного поля, без привлечения к объяснению соответствующих опытов правил левой и правой рук.
Антиподно − эквивалентная методика по объяснению электромагнитных явлений исходит из того, что фотоны или кванты электромагнитного поля, подобно электрическим зарядам бывают трёх разновидностей − условно γ + ; γ − и γ ° .
О том, почему автор рассмотрение электромагнитных явлений проводит с позиции этих квантов, Читатель узнает из самой статьи.
Предлагаемая Читателю статья предназначена учёным, инженерам, студентам и учащимся общеобразовательных школ, а также для всех, кто интересуется тайнами Природы.

Содержание статьи.

1. Предисловие
2. Предпосылки антиподно − эквивалентного подхода к электромагнитным явлениям.
3. Электрический диполь в однородном электрическом поле.
4. Отклонение движущихся заряженных частиц электрическим полем.
5. Взаимодействие магнитных полей, подобных магнитному полю полосового постоянного магнита.
5.1. Взаимодействие Южных магнитных полюсов полосовых постоянных магнитов.
5.2. Взаимодействие Северных магнитных полюсов полосовых постоянных магнитов.
5.3. Взаимодействие разноимённых магнитных полюсов полосовых постоянных магнитов.
6. Сила Лоренца.
6.1. Действие магнитного поля на движущийся заряд.
6.2. Движение положительного заряда − позитрона (е+ −на) в магнитном поле прямолинейного тока.
7. Электромагнитная индукция.
7.1. ЭДС индукции в движущихся проводниках.
7.2. Вращение проволочного витка (прямоугольной рамки) в однородном магнитном поле.
8. Контур с током и без в магнитном поле.
8.1. Контур с током в однородном стационарном магнитном поле.
8.2. Контур с током в неоднородном магнитном поле.
9. Правило Ленца и электромагнитная индукция.


1. ПРЕДИСЛОВИЕ

" В конце концов Математика ведь имеет
своё основание в Природе, она прямо−
таки призвана отражать в себе и описывать
Физику − так мудрено ли, что иногда
Математика намекает на то, что не в силах описать,
что ещё не поднесено к зеркалу достаточно близко,
чтобы там отразиться . . . "
Е. Вигнер − лауреат Нобелевской премии.

Прежде чем мы непосредственно перейдём к объяснению электромагнитных явлений с причинных позиций, коротко остановимся на вопросе методологического подхода к этим явлениям. И для того, чтобы Читателю было понятно, о чём идёт речь, приведу небольшую выдержку из элементарного учебника по физике под редакцией академика Г.С. Ландсберга т.2, М. , изд. "Наука", 1966 г., стр. 40:
" . . . Заметим, что в начале изучения электричества часто возникает стремление "объяснить" электрическое поле, то есть свести его к каким−либо иным, уже известным явлениям, подобно тому, как тепловые явления мы сводим к беспорядочному движению атомов и молекул.
Однако многочисленные попытки подобного рода в области электричества неизменно оканчивались неудачей. Поэтому мы считаем, что электрическое поле есть самостоятельная физическая реальность, не сводящаяся ни к тепловым, ни к механическим явлениям.
Электрические явления представляют собой новый класс явлений природы, с которыми мы знакомимся на опыте, и дальнейшая наша задача должна состоять в изучении свойств электрического поля и его законов".

По поводу этой выдержки уместно сказать, что уважаемый автор в отношении электрического поля придерживался позиции следствия, а не причины. Но как показала практика, подобный подход к этим (от авт.: тоже можно отнести и к магнитным) явлениям не способствовал причинному пониманию этих явлений, хотя на пути их изучения и были достигнуты впечатляющие успехи.
Исходя из сказанного, правомерен следующий вопрос: "Какими требованиями следует руководствоваться при изучении электромагнитных и других физических явлений, чтобы объяснить их физическую сущность (для начала, хотя бы в первом приближении)?"
Для примера покажем, как на данном этапе познания окружающей нас действительности объясняется опыт воздействия однородного магнитного поля на проводник с током: известно, когда в проводнике нет тока, он по отношению, напр., подковообразного магнита, неподвижен. При прохождении тока, он, в зависимости от направления тока в нём, будет или втягиваться в пространство между полюсами магнита, или наоборот − выталкиваться.
Всё объяснение данного опыта, его функциональной схемы, сводится к тому, что со стороны магнитного поля подковообразного магнита на проводник с током оказывается силовое воздействие. Реакция же проводника на это воздействие определяется по правилу левой руки.
Но что происходит в самом проводнике и в пространстве вокруг него? Ведь мало сказать, что внешнее магнитное поле оказывает силовое воздействие на проводник с током. Надо ещё и объяснить, посредством чего и как это происходит.
В отношении первого ясно. Электромагнитное взаимодействие, по современным представлениям осуществляется за счёт квантов электромагнитного поля, т. е. за счёт фотонов или в узком смысле − света, поскольку свет представляет собой электромагнитное излучение.
Ответа на вопрос − как это происходит, пока что нет. Вот и получается, что при всех наших знаниях об электромагнетизме, мы в отношении этого физического явления пребываем как бы в "некотором" неведении.
Вопрос: "Можно ли "выйти" из неопределённости такого состояния и если да, то как?"
Ответ: Можно. И чтобы это сделать, для начала обратимся к Математике, к разделу Арифметика, а вернее − к Натуральному ряду целых чисел (N). И вот тут, со стороны Читателя вполне правомерен следующий вопрос: " А какое отношение к электромагнетизму (тоже можно отнести и к гравитации) имеет этот математический ряд? Ведь электромагнетизм − это природное явление и рассматривается нами как соответствующая форма существования Материи, а Натуральный ряд целых чисел являет собой всего лишь абстракцию описательного плана и к данному явлению Природы не имеет вроде бы никакого отношения. Тем более, ведь в Природе такого образования нет!"

2. ПРЕДПОСЫЛКИ АНТИПОДНО-ЭКВИВАЛЕНТНОГО ПОДХОДА К
ЭЛЕКТРОМАГНИТНЫМ ЯВЛЕНИЯМ

Первое, что нам предстоит сделать, это ответить на вопрос: Сколькими формами можно записать этот ряд?
Ответ: В трёх формах. Первая − это целочисленная, монотонно возрастающая последовательность вида 1, 2, 3, 4, 5 и т. д. в + ∞ −ть (примечание: ∞ − символ бесконечности).
Вторая − в виде рациональных, антиподно − эквивалентных дробей. Вторая форма записи натурального ряда целых чисел ( N ) получается, если каждое число этого ряда представить в виде рациональных, эквивалентных дробей. При этом соблюдается следующее, обязательное эквивалентное условие : рациональная дробь, представляющая одно и тоже число, должна обладать одной и той же характеристикой. В качестве таковой выступает высота рациональной дроби по операции умножения числителя на знаменатель. Запись части ряда N от 1 −цы до 13 −ти, в соответствии с этим условием, приводится ниже. Здесь же даётся эта часть ряда в общепринятой, целочисленной форме записи.

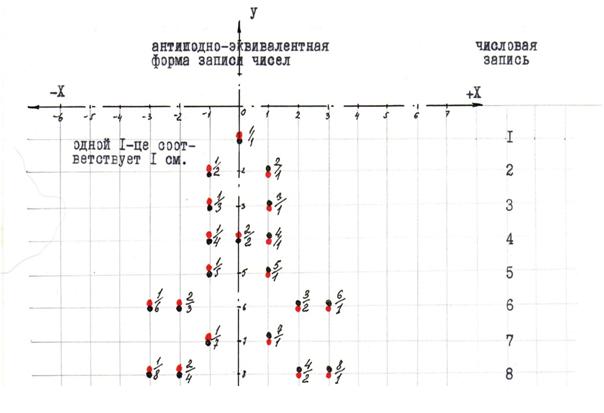
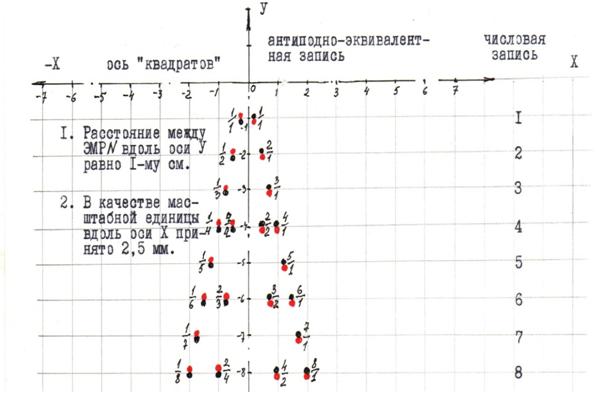
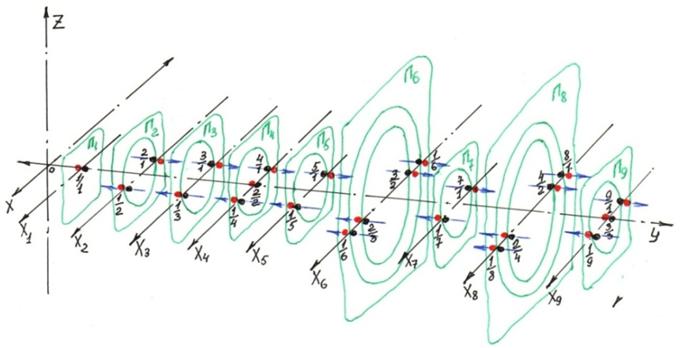
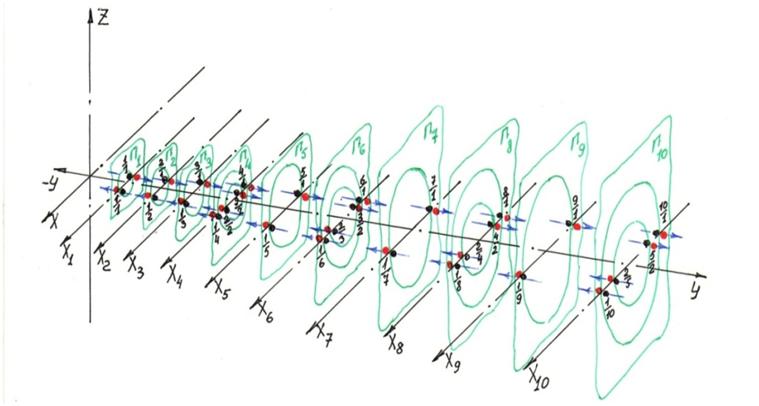
Антиподно−эквивалентная форма записи части ряда N


1/1

1/2 2/1

1/3 3/1

1/4 2/2 4/1

1/5 5/1

1/6 2/3 3/2 6/1

1/7 7/1

1/8 2/4 4/2 8/1

1/9 3/3 9/1

1/10 2/5 5/2 10/1

1/11 11/1

1/12 2/6 3/4 4/3 6/2 12/1

1/13 13/1

и т. д.


Целочисленная форма записи части ряда N

1

2

3

4

5

6

7

8

9

10

11

12

13

и т. д.

Третья форма записи этого ряда − это запись его по формуле а + Х² = N или по схеме "квадратной эквивалентности". В этой формуле а − числовой Фликкер выброс − см. ниже п.2; N − число из натурального ряда чисел; Х² − часть числа N, представляемая в квадратной форме − эта форма записи натурального ряда чисел была использована автором при написании работы "Математика, Календарь, Пирамиды", которая явилась отправным эпизодом в последующей работе под названием "ТЕОРИЯ КВАДРАТА".

А теперь отметим следующие особенности, присущие антиподно−эквивалентной форме записи ряда N:
1. Каждое число ряда N может быть записано (представлено) в виде рациональных дробей, у которых одна и та же высотная характеристика по операции умножения числителя на знаменатель. Такие дроби называются эквивалентным.

2. В структурной записи чисел по схеме антиподной эквивалентности имеется принципиальная разница. Так, напр., число 6 записывается в виде 1/6, 2/3, 3/2, 6/1, а число, напр. , 36 − в виде 1/36, 2/18, 3/12, 4/9, 6/6, 9/4, 12/3, 18/2, 36/1.
Отличие в антиподно − эквивалентной записи обоих чисел состоит в том, что в одном из них имеется дробь, у которой наблюдается равенство числителя знаменателю. Такая дробь называется "квадратной", ибо её по высотной характеристике можно интерпретировать как квадрат числа. В данном случае числа 6 −ти. А вот для числа 6 −ти и ему подобных, "квадратной" записи нет.
Такую запись можно осуществить искусственно, посредством добавления к "квадратной" дроби предыдущего числа, недостающего, которое впредь будем именовать Фликкер выбросом. В соответствии с этим, число 6 в "квадратной" форме запишется как 2 + 2/2, а сам ряд в виде 1/6, 2/3, 2 + 2/2, 3/2, 6/1.
То же самое относится ко всем числам из ряда N, а в общем и ко всем целым числам из − в + ∞ −ть, ибо ряд N является подмножеством ряда целых чисел Z.

3. Дроби 1/6, 2/3 по отношению дробей 6/1, 3/2, соответственно являются перевёрнутыми и по отношению друг друга являются антиподами. Это позволяет говорить, что любое число из ряда N может быть записано посредством "прямых" и "перевёрнутых" (или правильных и неправильных) антиподно−эквивалентных, рациональных дробей, являющихся по отношению друг друга антиподами.

4. Каждое число из ряда Z ( N ) может быть записано в виде антиподно−эквивалентных, рациональных дробей. При этом, если в ряде N число ( n ) записывается единичным способом, то с помощью данных дробей в виде соответствующего математического ряда, который в последующем будем называть как Эквивалентный Математический Ряд рациональных дробей или сокращенно ЭМР. Например, числу 36 будет соответствовать ЭМР36, а числу 6 ЭМР6 и т. д.
В целом ряд N состоит из n −го множества рядов ЭМРN и может быть записан в виде ЭМР(1 ÷ ∞). А так как этот ряд является подмножеством ряда Z, то и последний, с помощью ЭМРN, может быть записан в виде ЭМР(− ∞ ÷ ∞). Обе формы записи и будут нами задействованы в последующем.

5. Количество эквивалентных, рациональных дробей, входящих в состав того или иного ЭМРN, определяется количеством простых множителей, а также комбинацией их произведения, на которые можно разложить всякое составное число. То есть базой построения рядов ЭМРN является множество простых чисел, являющееся подмножеством ряда N:
1; 2; 3; 5; 7; 11; 13; 17; 19; 23 . . . . . . . . . . . 101 . . . . . . . 137 . . . . . . . 587 . . . . и т. д.

6. К особенности "квадратных" дробей следует отнести, с одной стороны, их положение в структурной схеме ЭМРN − они занимают в нём центральное положение, а с другой − они являют собой наиболее компактную ( сжатую ) форму записи числа n по операции умножения числителя на знаменатель.

7. Каждая дробь в ряде ЭМРN (ЭМРZ или ЭМР (− ∞ ÷ ∞)) занимает строго определённое местоположение. Пребывание её в других ЭМРN кроме "своего" не только не предусмотрено, но и "запрещено", и этот "запрет" определяется антиподно − эквивалентной сущностью схемы построения ЭМРN.

В плане наличия в структуре ряда ЭМР(1 ÷ ∞); (− ∞ ÷ ∞) антиподно−эквивалентного "запрета", регламентирующего правило (принцип) "заполнения" дробями числовых позиций, правомерно поставить следующий вопрос: "Имеется ли в Природе аналог подобному, антиподно − эквивалентному "запрету"?
Ответ: Да, в Природе имеется аналог математическому, антиподно − эквивалентному "запрету"! Это ни что иное как правило (принцип) В. Паули, "регламентирующее" порядок заполнения электронами электронных уровней в атоме.
В соответствии с этим принципом, на одной и той же орбите, в одном и том же состоянии не могут находиться одновременно два электрона (е− −на). В более строгой интерпретации правило (принцип) В. Паули − см., например, в учебнике по физике "Курс общей физики" авт. И.В. Савельев, т. 3, изд. "Наука", М. , 1982 г., стр. 128.

Таким образом, если в первом приближении исходить из предположения (предпосылки), что антиподно − эквивалентный "запрет" − это аналог пространственного запрета В. Паули, то мы вправе, исходя из антиподно − эквивалентной схемы построения ЭМР(− ∞ ÷ ∞) предполагать, что различие двух е− −ов, пребывающих на одном энергетическом уровне в атоме, определяется не только их пространственной ориентацией относительно друг друга − их спины (собственный механический момент импульса Мs) должны быть повёрнуты относительно друг друга в пространстве на 180°, но и (обращаю особо /!/ внимание Читателя) качественно отличаться внутренней структурой.
Сказанное позволяет (условно) наделить антиподно − эквивалентные, рациональные дроби рядов ЭМРN спиновой символикой и как в физике, изображать её в виде стрелок: ↑ − для прямых или правильных дробей и ↓ − для обратных или неправильных.

Далее, из практики мы знаем, что ряд N Математикой "задействован" в таком условном (графическом) построении, как система координат, в плоском и пространственном прямоугольном вариантах.
В отношении целочисленной формы записи ряда N просто: каждому числовому интервалу, равному 1 −це, ставится в эквивалентное соответствие отрезок определённой длины. В результате получается математический, условный объект, именуемый числовой прямой или осью. Две взаимно перпендикулярные числовые прямые и образуют на плоскости (условно) систему прямоугольных координат. Для пространственной необходимо наличие 3 −х, взаимно перпендикулярных числовых прямых, исходящих (заходящих) из (в) одной (−ну) общей (−ую) точки (−у), называемой началом (концом) координат.

Если практика использования ряда N в случае числовых прямых или осей в системах прямоугольных координат (обоих видов) давно известна, то в отношении ряда ЭМР(− ∞ ÷ ∞) подобной практики нет. В то же время следует заметить, что возможность использования ряда N для системы координат предопределяется возможностью отождествления целочисленного числа и числовой позиции с таким абстрактным понятием, как точка.
В отношении ряда ЭМР(− ∞ ÷ ∞) такой возможности просто нет, ибо нельзя все дроби, отдельно взятого ряда ЭМРN, стянуть в одну точку. Поэтому, исходя из этих соображений, мы можем говорить только о плоской и пространственной форме интерпретации этого ряда.

Сказанное в отношении ряда ЭМР(1 ÷ ∞ );(− ∞ ÷ ∞) предопределяет следующий вопрос:
"Имеется ли возможность "привязки" этого ряда к плоской и пространственной системам прямоугольных координат?".
Ответ: Да, имеется. При этом подобную "привязку" можно осуществить в 2 −х вариантах.

Во−первых, как и в случае целочисленной форме записи ряда N, каждую антиподно − эквивалентную, рациональную дробь в рядах ЭМРN изобразим в виде условной точки, состоящей как бы из двух подточек − красного и синего цвета.
Теперь, для "привязки" этих точек к координатной прямой (оси), нам нужно выполнить условие, определяемое антиподо − эквивалентной конструкцией самого ЭМРN : симметричность расположения дробей относительно дроби со структурой "квадрата".
Располагая дроби (соответствующие точки) со структурой "квадрата" непосредственно на координатной числовой прямой (оси) − по этому признаку подобную ось впредь будем именовать осью "квадратов", а остальные вне её, на перпендикулярном к ней направлении, мы получим новый, условный, математический объект, который можно именовать антиподно − эквивалентной, числовой координатной осью.
При этом условные точки (антиподно − эквивалетные рациональные дроби) будут относительно самой числовой оси (оси "квадратов") располагаться на расстоянии, которое оговаривается условным правилом, предопределяющим два варианта "привязки" ЭМРN к координатной оси − оси "квадратов".

Согласно первого, за расстояние от условной точки (соответствующей дроби) до оси "квадратов" примем у "прямых" (числитель меньше знаменателя) дробей числа в числителях и в знаменателях у "обратных". По второму варианту − значение знаменателей у "прямых" и числителей у "обратных". Выбирая затем для каждого из вариантов тот или иной масштаб и выполняя вышеназванные условия "привязки" ЭМРN, мы получим варианты плоской "привязки" ЭМР(1 ÷ ∞) к оси "квадратов".
В качестве примера, поясняющего методику построения обоих вариантов, рассмотрим "привязку" к числовой оси (оси "квадратов") ЭМР16.

Вариант 1.
ЭМР16 состоит из следующих дробей: 1/16, 2/8, 4/4. 8/2, 16/1.
В соответствии с вышеизложенным, расстояния условных точек (эквивалентных, рациональных дробей) до оси "квадратов" будут следующими: для дробей 2/8 и 8/2 − две масштабные единицы; для дробей 1/16 и 16/1 − три масштабные единицы. Расстояние между дробями 1/16 и 2/8, соответственно, между 16/1 и 8/2 будет равно одной масштабной единице. В отношении дроби со структурой "квадрата" мы уже определились. Она, в соответствии с конструкцией ЭМРN, располагается на координатной прямой (на оси "квадратов") − см. рис. 5.

Условно−графическое изображение натурального ряда целых чисел N в плоской,
прямоугольной системе координат посредством ЭМРN − (по варианту 1).

и т. д.

Рис. 5.

Вариант 2.
Методика "привязки" ЭМР16 к оси "квадратов" по этому варианту, подобна методике варианта 1 − см. рис. 7.

Условно−графическое изображение натурального ряда целых чисел N в плоской,
прямоугольной системе координат посредством ЭМРN − ( варианту 2).

и т. д.

Рис. 7.

Кроме указанных расстояний между условными точками − дробями в ЭМРN, укажем также и расстояние между самими ЭМРN вдоль оси "квадратов". Так как каждый последующий (предыдущий) ЭМРN получается из предыдущего (последующего) за счёт прибавления (вычитания) к нему (из него) 1 −цы (1/1), которая по отношению к каждому ЭМРN есть ни что иное, как соответствующий Фликкер выброс, то из этого следует, что все ЭМРN в ряде ЭМР(− ∞ ÷ ∞) в конструктивном отношении отстоят друг от друга вдоль оси "квадратов" на расстоянии одной масштабной единицы. При этом роль 1 −цы в операции прибавления (вычитания) к какому−либо числу (n) из ряда N по своему содержанию однозначна − чисто количественная. Число, записываемое в целочисленной форме, возрастает (убывает) на 1 −цу. В этом случае сторонний наблюдатель отслеживает только количественную сторону процесса.

Совсем иная роль "отводится" 1 −це (1/1) в случае прибавления ("захвата") или вычитания ("выброса") к тому или иному (из того или иного) ЭМРN. В этом случае за ней "закрепляются" две функции: одна, как и прежде − количественная, а другая − качественная.
С первой ясно: как и в случае с рядом N, ЭМРN возрастает (убывает) на 1 −цу. Со второй: "захват" или "выброс" её ЭМРN качественно отражается на его внутренней, антиподно − эквивалентной структуре. В нём происходит полная замена дробей новыми дробями, с иной антиподно − эквивалентной структурой из последующего или предыдущего ЭМРN (см. числовой интервал ЭМР(1 ÷ 13)).

Вышеназванные варианты можно интерпретировать и пространственно. Для этого поступим следующим образом, исходя из условия, что две антиподно − эквивалентные, рациональные дроби в рядах ЭМРN располагаются на одинаковом расстоянии от оси "квадратов": "обернём" (мысленно) ряд ЭМР(1÷ ∞) вокруг этой оси − достаточно произвести его поворот на 180°. В результате траектории движения точек замкнутся и в пределе получатся круговые траектории в виде колец (окружностей). На таких кольцеобразных траекториях точки (эквивалентные, рациональные дроби) равноудалены от оси "квадратов ( см. рис. 6 и 8 ). В последующем, подобные кольцеобразные траектории будем называть эквивалентными уровнями (Э.У.к.). При этом будем помнить, что каждый Э.У.к. в ЭМРN "содержит" по две антиподно − эквивалентные дроби (см. числовой интервал ЭМР(1 ÷ 13)).


Условно − пространственный вариант графической интерпретации части ряда
ЭМР(1 ÷ ∞) при вращении составляющих его антиподно − эквивалентных
структур (рациональных дробей, точек) относительно оси "квадратов" − оси У (по варианту 1).



Примечание: с целью наглядности, расстояния между ЭМРN увеличены.

Рис. 6




Условно−пространственный вариант графической интерпретации части ряда ЭМР(1 ÷
∞) при вращении составляющих его антиподно−эквивалентных структур (рациональных
дробей, точек) относительно оси "квадратов" − (по варианту 2).



примечание: с целью наглядности, расстояния между ЭМРN увеличены.

Рис. 8

Если теперь рисунок 6 и 8 сравним со схемой, условно изображающей лини индукции магнитного поля прямолинейного тока вокруг проводника, а также со снимком устройства галактики Геркулес А (см. рис. 9 и 10), то вынуждены в 1 −ом приближении констатировать их внешнее сходство по части графики.







Естественно возникает вопрос: "Чем обусловлено такое сходство?"
Оставим ответ на этот вопрос пока открытым, а сейчас отметим, что условным (абстрактным линиям индукции магнитного поля прямолинейного тока и конфигурации галактики Геркулес А в просторах Вселенной, в Математике есть абстрактный аналог в виде кольцевых (условно) траекторий антиподно − эквивалентных, рациональных дробей ряда ЭМР(− ∞ ÷ ∞); (1 ÷ ∞) вокруг координатной оси "квадратов", в пространственной системе прямоугольных координат.

Это обстоятельство "приводит" нас к следующей мысли: так как ряд ЭМР(− ∞ ÷ ∞ ) является антиподно − эквивалентным (абстрактным) образованием, основой построения которого есть антиподная эквивалентность, то магнитное поле вокруг проводника с током и конструктивное построение галактики Геркулес А следует анализировать с тех же позиций, проявляя к ним антиподно − эквивалентный подход.
Одновременно с этим, так как схема построения рядов ЭМРN в ряде ЭМР(− ∞ ÷ ∞) едина из − в + ∞ − ть, то это означает, что соответствующий антиподно − эквивалентный анализ вышеуказанных образований следует проводить в строгом соответствии с принципом Единства и Подобия (пр.Е и П −ия !).
А так как в нашем распоряжении имеется только ряд ЭМР(− ∞ ÷ ∞), то сделав ему соответствующий структурно − функциональный, антиподно−эквивалентный анализ, мы тем самым, в первом приближении, получим ответы на вопросы не только в отношении магнитного поля вокруг проводника с током и галактики Геркулес А, но также и в отношении того же электрона, позитрона и т. д., и наконец, в отношении нашей планеты Земля (примечание: в данной статье речь преимущественно будет идти об электромагнитных явлениях).
Первая часть подобного анализа будет приведена в данной статье; вторая будет дана отдельной статьёй, с последующим размещением в Интернете.

А теперь вновь обратимся к ряду N. В этом ряде каждая последующая или предыдущая числовая позиция получается за счёт операции прибавления или вычитания 1 −цы. При таком количественном подходе к ряду N, 1 −ца не "несёт" никакой функциональной "нагрузки" и в своей основе является абстрактным, математическим символом.
Но исторически сложилось так, что в практических целях за 1 −ей и не только за ней, люди "закрепили" ту или иную физическую величину: параметр, функцию и т. д. Закрепляя, напр., за ней пространственную функцию, появляется возможность измерять пространственные интервалы (расстояния). Если же временную функцию − время и т. д. То есть с помощью 1 −цы и т. д. можно количественно сравнивать разные части единого целого, будь−то пространство, время, скорость, вес и т. д. Однако, всё это есть частный случай, так как ряд N не рассматривается как функциональное, абстрактно − математическое образование, которое может "функционировать" (мысленно, с точки зрения стороннего наблюдателя) в Пространстве и во Времени.

И вот тут, как только к ряду ЭМР(− ∞ ÷ ∞) подходим с этих позиций, то в функциональном отношении 1 −ца (1/1) "становится" ничем иным, как Фликкер выбросом, т. е. подобием излучения, которое можно поглощать или излучать (изымать из окружающего пространства или наоборот − выбрасывать в него).
То есть 1 −ца (1/1), как функционально − абстрактный, математический символ (объект) "переходит" в разряд Фликкер выбросов. Это понятие в смысловом отношении объединяет всебе все виды излучений, поглощений, происходящих в материальных, антиподно − эквивалентных взаимно связанных системах как в окружающем нас Мире, так и в нас самих − людях.

Из сказанного можно заключить, что оперировать 1 −цей (и не только ей) можно с двух позиций (позиция дуализма): или с позиции абстрактно − математического объекта, характеризуя количественную сущность того или иного материального (в том числе и абстрактного) объекта,или с позиции Фликкер выброса, когда 1 −ца (и не только она) отождествляется с частью той материальной (или абстрактной) системы, которая излучается (выбрасывается) − поглощается (изымается) ею в процессе функционирования в Пространстве − Времени в момент её перехода из одного антиподоно − эквивалентного, взаимосвязанного состояния в другое. Другими словами − в более сжатое, компактное или наоборот, в более расширенное состояние. В первом случае материальная (абстрактная) система будет развиваться в Прошлое, а во втором в Будущее.

Если же теперь мы удалим из своих рассуждений 1 −цу (и т. д.) и будем оперировать соответствующим материальным (абстрактным) Фликкер выбросом при рассмотрении функциональной схемы той или иной антиподно − эквивалентной, материальной (в том числе и абстрактной) системы, то появится возможность любое природное явление, физический процесс и т. д. рассматривать с одной и той же функциональной позиции − позиции Фликкер выброса.
К сказанному о Фликкер выбросе следует добавить и то, что в схеме ряда ЭМР(− ∞ ÷ ∞) он, в виде антиподно − эквивалентной 1 −цы (1/1) "выбрасывается" одним ЭМРN и "поглощается" затем другим (по направлению оси "квадратов"). При этом имеет место внутриструктурное преобразование дробей в них обоих. В результате получается, что один ЭМРN (образно) воздействует на другой не непосредственно, а посредством Флликкер выброса, через разделяющее их пространство.
Это позволяет Флликкер выброс классифицировать как объект (абстрактный в математическом ряде ЭМР(− ∞ ÷ ∞); материальный в той или иной соответствующей антиподно − эквивалентной, материальной системе), выполняющий посредническую функцию, то есть передающий действие от одного объекта другому или обеспечивающий взаимодействие между объектами.
Естественно, что на каждом антиподно − эквивалентном, материальном уровне из − в + " ∞ " −ть *), должны присутствовать только свои, присущие для этого уровня посредники (примечание: так, для антиподно − эквивалентного уровня е− −ов и е+ −ов, таковыми являются кванты электромагнитного поля; для кварков − это глюоны, являющиеся переносчиками сильного взаимодействия; в случае гравитационного − это гравитоны и т. д.).
- - - - - - -


*) " ∞ " − конечная бесконечность. Математический абстрактный символ, указывающий на конечность какого−либо очень большого или очень малого параметра, характеризующего ту или иную физическую и т. д. величину, без конкретного указания её истинного значения в количественном выражении. Так, например, говорят о том, что силовые линии напряжённости электрического поля, начинающиеся на положительных зарядах, уходят от них и заканчиваются в ∞ −ти на отрицательных. Но как бы велико или мало не было расстояние между зарядами, само по себе оно конечно. Этим абстрактным, математическим символом удобно пользоваться как в − −с, так и в + −с " ∞ " −ти, имея в виду конкретно неопределённый очень или большой, или очень малый масштабный фактор.
- - - - - - -

Забегая несколько вперёд, особенно это следует отметить в отношении 4 −х видов взаимодействий − электромагнитного, ядерного (сильного), слабого и гравитационного.
В отношении первых трёх ясно: для электромагнитного − это фотоны (кванты электромагнитного поля); в сильном − это глюоны, являющиеся переносчиками сильного взаимодействия между кварками; в слабом − это векторные бозоны W+, W− и Z °. А вот для гравитационного взаимодействия кандидата в Природе учёными пока не обнаружено. Предположительно, в качестве такового "выступает" гравитон − частица с нулевой массой и спином 2.

С учётом того, что базовым лейтмотивом данной статьи является антиподная эквивалентность, то в последующем, эта тройственная схема посредников (W+, W− и Z ° для слабого взаимодействия) и будет, в соответствии с принципом Единства и Подобия использована при рассмотрении причинной стороны электромагнитных явлений. В соответствии с этим замечанием, в качестве переносчика электромагнитного взаимодействия, в статье будут задействованы следующие антиподные фотоны: γ + , γ − и γ°.
В отношении данной символики необходимо дать соответствующие пояснения:
Современной теорией, последовательно описывающей взаимодействия фотонов, электронов и позитронов, а также мюонов с учётом их возможных взаимопревращений, является квантовая электродинамика. Она рассматривает электромагнитное взаимодействие между заряженными частицами как процесс обмена виртуальными фотонами. Считается, что электростатическое поле заряженной частицы обусловлено испусканием и поглощением ею виртуальных фотонов − так называемое дельбрюковское рассеяние − см. Маленькая Энциклопедия, "Физика Микромира", гл. редактор чл. − кор. АН СССР Д.В. Ширков, изд. "Советская Энциклопедия", М., 1980 стр. 93, "Рассеяние света на свете".

Фотоны различаются по энергии. Так фотоны с энергией > 100 Кэв обычно называют γ −ма квантами. Оказалось, например, что в электростатическом поле атомного ядра фотон с энергией > 1 Мэв может превратиться в электрон и позитрон (процесс рождения пары) и наоборот, столкновение электрона и позитрона приводит к превращению их в два (или три) γ −ма кванта (аннигиляция пары).
С учётом того, что в статье, с причинных позиций будут анализироваться функциональные схемы взаимодействия как электрических зарядов, так и магнитных полей, автор при обозначении квантов электромагнитного поля использует общепринятое обозначение фотонов в виде γ .
В то же время, так как анализ функциональных схем взаимодействия электрических зарядов, магнитных полей, а также магнитного поля с электрическими зарядами, будет проводиться с антиподных позиций, то необходимо при анализе использовать антиподные γ −ма кванты. Их антиподность будет характеризоваться знаком + и знаком −. Нейтральный γ −ма квант наделяется знаком ° .

А теперь, прежде чем мы приступим к рассмотрению ряда ЭМР(− ∞ ÷ ∞) с позиции Фликкер выброса, т. е. к структурно − функциональному анализу (примечание: функциональный от слова функционировать, когда соответствующая антиподно − эквивалентная материальная или абстрактная система, по соответствующей функциональной схеме, развивается в Пространстве − Времени от одного качественного состояния до другого) этих рядов, необходимо обратить внимание Читателя на методику подобного анализа. )*
- - - - - - -

)* примечание: отдельные фрагменты этого анализа будут даны в этой статье; основная же часть этого анализа будет дана отдельной статьёй, в которой пойдёт речь об анализе рядов ЭМРN и ЭМР(1 ÷ ∞).
- - - - - - -

Суть этой методики заключается в том, что сторонний наблюдатель рассматривает эти ряды как неподвижные, статические образования (условно), а о "процессах" ("событиях") в отношении антиподно − эквивалентных, рациональных дробей судит в результате своего мысленного "перемещения" вдоль этих рядов. При этом движение в сторону возрастания ЭМРN будем рассматривать как движение в Будущее, а в обратную − в сторону убывания ЭМРN (т.е. в направлении начала координат), как движение в Прошлое.

Однако, учитывая принцип дуализма, логически − абстрактные построения в отношении этих рядов будем производить, применяя совсем противоположную методику. Будем считать стороннего наблюдателя и сами ряды неподвижными относительно друг друга (конечно условно, как например , в случае со звёздами и т. д.), а "подвижными" в рядах будут ЭМРN, дроби и Фликкер выбросы.
Используя такую методику, в ряде ЭМР(− ∞ ÷ ∞) мы будем "наблюдать" следующие процессы (события):
1. Перемещение антиподно − эквивалентных, рациональных дробей в рядах ЭМРN по соответствующей функциональной схеме.
2. Перемещение антиподно − эквивалентных, рациональных дробей, "квадратов" (Фликкер выбросов), ЭМРN в Будущее при отсутствии аналогичного перемещения их в Прошлое.
3. Перемещение антиподно − эквивалентных, рациональных дробей, "квадратов" (Фликкер выбросов), ЭМРN в Прошлое при отсутствии аналогичного перемещения их в Будущее.
4. Одновременное перемещение антиподно − эквивалентных, рациональных дробей, "квадратов" (Фликкер выбросов), ЭМРN вдоль оси "квадратов" в обеих (взаимно встречных) направлениях − и в Будущее, и в Прошлое. То есть математический ряд ЭМР(− ∞ ÷ ∞) образно или абстрактно "работает" (функционирует) в режиме двух встречных, соответствующих антиподных потоков.

После ознакомления с предыдущей частью статьи, у Читателя мог возникнуть следующий вопрос: "О каком функциональном анализе может идти речь в отношении натурального ряда целых чисел ( N )? Ведь данный математический ряд являет собой искусственное, абстрактное образование, не имеющего какого бы то ни было отношения не только к электромагнитным явлениям, но и вообще, к электричеству (добавим и к гравитации)?"
Как это ни странно, но Читатель в какой−то степени прав. А потому правомерен следующий вопрос: "Чем следует мотивировать проведение такого анализа?"
Ответ: В определённой степени Читатель прав, но только частично, ибо о ряде N судит по его целочисленной форме записи, не имея в виду его вторую, антиподно − эквивалентную. Эта же форма в корне отличается от предыдущей и в отличии от неё позволяет рассматривать ряд ЭМР(− ∞ ÷ ∞) и ряды ЭМРN, как антиподно − эквивалентные системы, которые, с точки зрения стороннего наблюдателя, могут "функционировать" (развиваться) в Пространстве и во Времени.

Вопрос: "Какие события будут "происходить" в ряде ЭМР(− ∞ ÷ ∞ ), если Фликкер выброс в форме 1 −цы (1/1) будет "перемещаться" вдоль оси "квадратов" в направлении из + " ∞ " −ти к т. О (началу координат), т. е. в направлении из Будущего в Прошлое?"
Ответ: По мере продвижения Флликкер выброса вдоль оси "квадратов", каждый, "встречающийся" на его пути ЭМРN, "поглощает" (захватывает) 1 −цу (1/1). В результате его числовая масса возрастает на 1 −цу и он "перемещается" вдоль оси "квадратов" в Будущее на следующую числовую позицию. При этом особо следует отметить, что "перемещение" рядов ЭМРN в Будущее возможно только при наличии "перемещающегося" по (вдоль) оси "квадратов" соответствующего Фликкер выброса.
В случае с ЭМРN − это 1 −ца (1/1). В Природе − это те или иные материальные образования как в − −с, так и в + −с " ∞ " −ти. Так, например, в случае с е− −ми или е ? ‾ ми, таковыми являются кванты электромагнитного поля или фотоны света (примечание: какие именно − об этом речь будет идти далее); а вот в случае с кварками, таковыми являются глюоны и т. д.
Когда же ЭМРN "излучает" (выбрасывает) Фликкер выброс, то он относительно оси "квадратов" "движется" в направлении к т.О (началу координат) или же в Прошлое. То есть Фликкер выброс "излучается" ЭМРN в направлении возрастания ЭМРN, а сам ЭМРN "перемещается" на предыдущую числовую позицию, ближе к т.О − началу координат. Подобное "движение" Фликкер выбросов и ЭМРN в ряде ЭМР(− ∞ ÷ ∞) можно интерпретировать как реактивное движение.

Эти два абстрактных (с точки зрения стороннего наблюдателя) однонаправленных процесса "движения" ЭМРN и в Будущее, и в Прошлое вдоль оси "квадратов", с позиции Фликкер выброса можно интерпретировать несколько иначе: при "захвате" ("поглощении") Фликкер выброса, ЭМРN делает "отскок" в направлении от т.О (начала − конца координат) в + " ∞ " −ть; при "излучении" ("выбросе") Фликкер выброса наоборот, ЭМРN делает "подскок" в направлении из + " ∞ " −ти к т.О (началу − концу координат). При "захвате", ЭМРN "перескакивает" на следующую числовую позицию, а при "выбросе" − на предыдущую.
Одновременно с этим, соответствующий Фликкер выброс, представляющий собой (условно) соответствующий "квадрат" (или же соответствующий материальный объект, находящийся в "квадратном", т. е. в наиболее сжатом, максимально упакованном или уплотнённом состоянии), перемещается между ЭМРN в противоположных, соответствующих направлениях и это "перемещение" происходит строго по (вдоль) оси "квадратов", т. е. по направлению с "квадратной" проводимостью.
Перемещение Фликкер выброса по оси "квадратов" исключает наличие у него зарядовой принадлежности, т. к. он сам состоит из двух антиподных половин (или соответствующих структур). То есть на оси "квадратов" он пребывает в нейтральном состоянии и это состояние условно отмечается знаком ° . Например нейтральный гамма квант γ ° .
А так как это направление или путь, "проходимый" Фликкер выбросами между ЭМРN вдоль оси "квадратов", преодолевается в Пространстве, то его можно рассматривать как соответствующую, путевую перемычку между ЭМРN и условно обозначать символом Л.П. − луч перемычка (см. условный рис. 12).




С учетом же того, что "движение" как самих ЭМРN, так и самих Фликкер выбросов по направленности "осуществляется" во взаимно встречных направлениях, то и направленность движения вдоль Л.П. − осям "квадратов", должна характеризоваться разнонаправленностью. По одним движение должно осуществляться в одном направлении, по другим − в противоположном. В соответствии с этим, как Фликкер выбросы, так и ЭМРN, по отношению друг друга тоже должны иметь соответствующие отличия. Условно (абстрактно), это можно отобразить (маркировать) в виде знаков плюс ( + ) и минус ( − ).
Так, если в одну сторону вдоль Л.П. (вдоль соответствующей оси "квадратов" или соответствующей, проводящей среде) движутся Фликкер выбросы со знаком + −с, то в противоположную сторону, но уже по другим Л.П., должны двигаться Фликкер выбросы со знаком минус ( −).
Подчеркнём, что подобное взаимно противоположное движение должно осуществляться по разным, только для каждого из ЭМРN "разрешённым" (Природой) направлениям или по взаимно встречным Л.П. − как и в обычной жизни (пр. Е и П −ия!).
В отношении ЭМРN, которые будут "двигаться" вдоль Л.П. или оси "квадратов" навстречу Фликкер выбросу со знаком + −с, будут маркироваться знаком − − с (ЭМРN−); если навстречу Фликкер выбросу со знаком − −с, соответственно знаком + −с (ЭМРN+). О физическом "содержании" обоих знаков для Фликкер выбросов и ЭМРN речь пойдёт далее, а пока что, на данном этапе разговора об электромагнитных явлениях, будем их соотносить лишь с направлением движения первых в пространстве вдоль Л.П − вдоль осей "квадратов".

В пространственных, прямоугольных системах координат, Л.П. или оси "квадратов" являют собой абстрактное, математическое образование, вдоль которых "распространяются" (располагаются) ряды ЭМР(− ∞ ÷ ∞). В Пространстве же, подобные направления должны материализоваться соответствующим образом и, с одной стороны, иметь в нём соответствующую протяжённость, а с другой − очень малый поперечный размер вдоль всего пути распространения.
Малый их поперечный размер обусловлен тем, что по Л.П. − направлениям с "квадратной" проводимостью, в Пространстве должны (не только должны, но и перемещаются соответствующие материальные образования в фазе "квадрата", т. е. в наиболее сжатом, максимально упакованном, компактном состоянии − например, те же нейтронные звёзды) перемещаться материальные объекты в очень сжатом, максимально упакованном состоянии. О том, каким образом это состояние функционально достигается, речь пойдёт далее, при проведении структурно − функционального, абстрактного анализа ряда ЭМРN.
Представляется, что абстрактные Л.П., о которых идёт речь в статье, в рамках антиподно − эквивалентной Математики, с наличием у них признаков − протяжённости и малого поперечного размера, в действительности как раз и являют собой те "космические струны", о которых дискутируют учёные. От себя же отметим (с позиции пр. Е и П −ия!), что подобных Л.П. или "соответствующих космических струн" в иерархии Космоса из − в + " ∞ " −ть должно быть " ∞ " −ое множество. И ярким примером в этом отношении являются такие Л.П. между Галактиками ( см. доклад Љ81 "Космические чудеса, доступные нашему взору" авт. к.т.н. Алексей Воробьёв; доклады лаборатории "ИНВЕРСОР", журнал "Техника Молодёжи" Љ7 за 1983 г.)
В качестве примеров из этой статьи ниже приводятся два снимка:




А теперь вопросы:
1. Наблюдается ли в Природе процесс отскока − подскока, подобного абстрактному процессу с рядами ЭМРN в ряде ЭМР(− ∞ ÷ ∞)?
2. Наблюдается ли в Природе процесс взаимно встречного движения, подобного взаимно встречному "движению" ЭМРN и Фликкер выбросов в ряде ЭМР(− ∞ ÷ ∞)?

Ответы:
1. Процесс отскока − подскока, например, имеет место в случае с е− −ми в атомах. Общеизвестно, что при захвате (поглощении) фотона света (γ −та) е− −он делает отскок от ядра и перемещается (перескакивает) на последующий энергетический уровень. При выбросе (излучении) фотона света наблюдается противоположный процесс. Электрон делает подскок к ядру и смещается при этом на предыдущий энергетический уровень.
2. В подтверждение наличия в Природе взаимно встречного движения различных и в то же время подобных, соответствующих материальных потоков, можно привести много примеров и одним из таковых является пример прохождения электрического тока в электролитах.
По современным представлениям, электрический ток в проводниках и электролитах трактуется как направленное движение электрических зарядов под действием внешнего (стороннего) электрического поля, прикладываемого к проводнику. При этом те заряды, которые движутся против поля, условно считают отрицательными, а по полю − положительными. Таковыми в проводниках 1 −го класса, в которых электрический ток не вызывает химических действий, являются отрицательные е− − ны. В проводниках 2 −го, которые под действием электрического тока разделяются на составные части, добавляются ещё и положительно заряженные ионы.

Известно, что носители отрицательных электрических зарядов в проводниках и электролитах (т. е. проводниках 2 −го класса) движутся навстречу или против электрического поля, а положительные − по полю.
Исходя из этого, объективного, причём опытным путём подтверждённого факта, соответствующие полевые (материальные) структуры электрического поля, т. е. фотоны света (γ −ты), должны отличаться не только по направлению движения вдоль проводящей среды, но и быть отличными в функциональной направленности по отношению электрических зарядов. Одних они "заставляют" двигаться против электрического поля, других − по его направлению.
По этой причине впредь будем считать объективным наличие в Природе (а в общем, в окружающей нас действительности из − в + " ∞ " −ть − пр. Е и П −ия!) не только функционально противоположных, причём различных Фликкер выбросов, соответствующих материальных ЭМРN, но и объективным наличие в ней путей (Л.П.) с "квадратной" проводимостью. То есть путей, по которым взаимно встречно перемещаются в Пространстве (более предметно − в проводящей среде) не только те или иные материальные образования, но и соответствующие материальные Фликкер выбросы, которые по отношению первых (поглощающих или излучающих их) можно интерпретировать в виде соответствующей для них "пищи".
В случае электрических и магнитных полей, Фликкер выбросами являются кванты электромагнитного поля. Их "потребителями" − электроны, соответствующие ионы+, ионы− и т. д. И теперь, с учётом антиподно − эквивалентных соображений, высказанных выше при рассмотрении электромагнитных явлений, впредь будем исходить из объективного наличия в Природе Фликкер выбросов со знаком + −с и со знаком − −с.
В соответствии с этим, фотоны света, являющиеся полевыми частицами электрического и магнитного полей, будем подразделять на γ + и γ − и с этих позиций рассматривать взаимодействие не только электрических зарядов, но и по той же функциональной схеме и магнитных полей (пр. Е и П −я!). К этим двум разновидностям гамма квантов, как и в случае с тройственной схемой векторных бозонов (пр. Е и П −ия), следует "добавить" ещё и нейтральный гамма квант (γ ° ). О необходимости наличия такового, речь будет идти при структурно − функциональном анализе ряда ЭМРN(− ∞ ÷ ∞).

Исходя из сказанного, кванты с чисто магнитной функцией, будем обозначать как кванты γ +(м) и γ − (м); с чисто электрической как кванты γ +(эл) и γ − (эл). Первые обеспечивают передачу магнитного взаимодействия при взаимодействии магнитных полей, а вторые электрических. Подобное разделение является чисто условным и в одном случае, электрические могут выполнять функцию магнитных, а магнитные электрических и наоборот. О том, когда это происходит, речь пойдёт далее в статье. К этим двум разновидностям квантов необходимо будем добавить и виртуальные кванты γ +(в) и γ − (в). По наличию таковых в окружающем нас пространстве, мы будем исходить из положения Квантовой теории поля, согласно которой, в окружающем пространстве постоянно присутствуют эти разновидности квантов или фотонов.

А теперь, прежде чем будет дано объяснение различных электромагнитных явлений с причинных позиций, в отношении Л.П. − путей с "квадратной" проводимостью и "перемещающихся" (с точки зрения стороннего наблюдателя) вдоль них как соответствующих материальных ЭМРN, так и материальных Фликкер выбросов, выскажем следующее соображение:
выше, говоря о функциональной предназначенности Фликкер выброса, было сказано, что основным его предназначением является передача через разделяющее ЭМРN Пространство воздействия от одного ЭМРN к другому. При этом "поглощение" − "излучение" Фликкер выброса приводит к перемещению ЭМРN в Пространстве − подчеркнём: по выделенному в нём направлению, по направлению оси "квадратов". При этом сам ЭМРN всё время сохраняет свою ориентацию по отношению оси "квадратов". Плоскость, в которой располагаются (условно) его антиподно−эквивалентныее Э.У.к. , остаётся перпендикулярной к оси "квадратов", на всём пути следования (перемещения) вдоль неё.
Но тут, вполне правомерен следующий вопрос: "А под воздействием чего перемещается вдоль Л.П. и сам Фликкер выброс? Или какой материальный объект в − "∞ " −ти "несёт" функцию Фликкер выброса по отношению к нему?" Ведь с позиции принципа Единства и Подобия и сам Фликкер выброс, "питающий" ЭМРN, тоже должен "питаться" соответствующим, предназначенным для него Фликкер выбросом.
Другими словами, Фликкер выброс должен взаимодействовать с Л.П. или "питаться" из него соответствующими, материальными структурами, "получая" от них реактивный импульс для своего движения вдоль Л.П. в ту или иную сторону.
Но рассуждая подобным образом, мы вправе спросить: "А как отразится подобное взаимодействие Фликкер выброса с Л.П. на положение последнего в Пространстве?"

Ответ может быть следующим:
1. Если Л.П. материально не реализован в пространстве, а является своего рода проводящей средой, то при движении вдоль него Фликкер выброса (тоже и ЭМРN) он не будет подвергаться реактивному воздействию с их стороны.

2. Если же Л.П. каким − то образом (?) материализован в пространстве, то перемещающийся вдоль него Фликкер выброс (тоже и ЭМРN) будет реактивно с ним взаимодействовать и сообщать ему реактивный импульс в противоположном своему движению направлении.
Этот пункт, в своей основе, как бы предопределяет не растяжимость Л.П. по всей его длине и при получении им реактивного импульса от соответствующих Фликкер выбросов должен смещаться в пространстве в ту или иную сторону.
Если же вдобавок и сам Л.П. жёстко фиксирован на каком−либо материальном объекте, то при получении им реактивного импульса, Л.П. будет передавать этот импульс и самому объекту, заставляя его или смещаться в пространстве в ту или иную сторону, или поворачиваться в нём. То есть Л.П., при наличии не растяжимости, будет или "тянуть" соединённый с ним соответствующий материальный объект, или "отталкивать" его.
Но для того, чтобы подобное имело место в действительности, необходимо, чтобы Л.П. или пути с "квадратной" проводимостью, во−первых, объективно существовали в пространстве (исходя из пр. Е и П −ия, из − в + " ∞ " −ть); во−вторых − были "привязаны" к материальным объектам; в−третьих − обладали протяжённостью в Пространстве при наличии очень "малых" поперечных размеров.
Условно, подобные Л.П. можно интерпретировать в виде "линий" в Пространстве, исходящих из одних материальных тел, образований и входящих в другие. Или же в одном и том же материальном теле из одного его места они "выходят", а "заходят" в другом. А так как по подобным "линиям" (Л.П.) перемещаются в Пространстве соответствующие материальные объекты в максимально сжатом ("квадратном") состоянии, при наличии которого они не излучают или не делают в окружающее их Пространство надлежащих Фликкер выбросов (например, тех же γ −ов), то такие Л.П. для стороннего наблюдателя будут невидимы. Их наличие может подтверждаться опосредованно, находящимися около них материальных объектов, которые излучают соответствующие Фликкер выбросы.
Вопрос: "Не наличие ли этого фактора и позволяет обнаруживать Лучи Перемычки между Галактиками? Ведь вдоль этих галактических Л.П. располагаются те же звёзды! А там, где их нет, вроде бы и нет галактических путей?" В то же время, если в этом вопросе руководствоваться пр. Е и П −ия, то галактические Л.П. должны быть у всех Галактик, где бы и в какой части Вселенной они ни находились!
В окружающей же нас действительности, на роль подобных Л.П. "претендуют" (в первую очередь) линии напряжённости электрических полей и линии магнитной индукции магнитных. К подобным же Л.П. следует отнести и меридианы − линии или пути в человеческом организме, по которым, согласно концепциям древневосточной философии и медицины циркулирует специфическая энергия ("чи"). Древневосточные медики полагали, что в организме имеется энергия двух видов − внутренняя и особая, причём каждый вид энергии циркулирует по собственным путям (линиям, каналам, меридианам). Более подробную информацию о концепциях древневосточной философии и медицины, в том числе и о Теории Инь − Ян, см. "Руководство по иглорефлексотерапии", авт. Д.М. Табеев, изд. "Медицина", М., 1980 г.

А теперь, изложив вкратце методологию антиподно − эквивалентного подхода к электромагнитным явлениям, можно перейти к их объяснению с причинных позиций, без привлечения для этого искусственных правил, типа правила левой и правой рук. Но прежде, высказанные выше соображения методологического характера, выпишем в виде отдельных постулатов, которыми и будем руководствоваться при анализе функциональных схем взаимодействия электрических и магнитных полей.

1. Силовые линии или линии напряжённости электрического поля, а также линии магнитной индукции магнитного поля, объективно существуют в Пространстве − Времени и являют собой выделенные в нём направления, вдоль которых и по которым перемещаются соответствующие материальные образования в нормальном, не сжатом состоянии, а также в сжатом, "квадратном" состоянии. В случае электрических и магнитных полей − это фотоны света или кванты электромагнитного поля γ + , γ − и γ °.
2. Л.П. или линии напряжённости электрического и магнитного полей (примечание: последние, исторически называются линиями магнитной индукции) жёстко "привязаны" в Пространстве к тем или иным материальным образованиям, фиксированы относительно них и нерастяжимы по всей длине.
3. В случае электрических полей, Л.П.эл. − это "линии" "∞ " −но − конечной протяжённости в Пространстве, исходящие из одного вида электрических зарядов или заряженных тел и заканчивающихся в "∞ " −ти на другом, противоположном электрическом заряде или противоположно заряженном теле.
4. В случае магнитных полей, Л.П.м. − силовые линии магнитного поля или линии магнитной индукции, "выходят" из одного магнитного полюса, например, из Северного, и "входят" в противоположный − в Южный магнитный полюс. Одновременно и из Южного магнитного полюса, тоже "выходят" (образно) "южные" Л.П.м. − линии магнитной индукции, а заканчиваются они в Северном магнитном полюсе.
5. Электрическое поле, в пространстве вокруг положительного электрического заряда, образовано двумя видами Л.П.эл. − линиями напряжённости. Из заряда выходят Л.П.эл. , по которым и вдоль которых перемещаются γ + (эл) кванты. Но одновременно с этим, в него входят такие же Л.П.эл., но от отрицательного электрического заряда, находящегося от первого (условно) в + " ∞ " −ти. По этим или вдоль этих Л.П.эл. перемещаются γ ‾(эл) кванты. В соответствии с представлениями квантовой электродинамики, γ (эл) кванты обоих типов являют собой виртуальные фотоны, т.е. γ +(в) и γ −(в).
В случае с отрицательным электрическим зарядом дело обстоит наоборот − из него выходят Л.П.эл. − линии напряжённости, по которым или вдоль которых перемещаются γ ‾(эл) кванты, а в него входят линии напряжённости или Л.П.эл. от положительного электрического заряда, вдоль которых перемещаются γ +(эл) кванты.
6. Магнитные силовые линии или линии магнитной индукции, подобно линиям напряжённости электрического поля (пр. Е и П −ия!), являются выделенными путями в Пространстве − Времени, по которым или вдоль которых также перемещаются γ + (м) и γ ‾(м). По Л.П.м, выходящим из Северного магнитного полюса, перемещаются γ ‾(м), а из Южного − γ + (м).
7. Фликкер выбросы, типа γ + и γ ‾, перемещаясь вдоль или по предназначенному для них Л.П. − по линиям напряжённости электрических полей или линиям магнитной индукции, реактивно с ними взаимодействуют, передавая им определённой величины реактивный импульс. Импульсы, через посредство Л.П. , передаются тем или иным материальным образованиям, заставляя их перемещаться в Пространстве − Времени или вращаться в нём.
8. Линии магнитной индукции магнитного поля прямолинейного тока, в соответствии с антиподно − эквивалентными представлениями о взаимно встречном движении Фликкер выбросов по круговым Л.П.к.(Э.У.к.), будут представлять собой систему взаимно встречных, охватывающих провод концентрических окружностей или Э.У.к. (см. рис. 13).


Љ рисунка 13

9. Картина взаимодействия γ + ; γ − и Л.П. на (условных) функциональных схемах электрического и магнитного, а в общем случае электромагнитного взаимодействия, условно будет изображаться в виде малых, искривлённых стрелочек, располагающихся рядом с (или вдоль) Л.П. по его направлению. Подобная схема условно представлена на рис. 14 см. ниже.







10. Направление перемещения γ +(м) и γ −(м) квантов по кольцевым (концентрическим) Л.П.к. или по Э.У.к. − линиям магнитной индукции, должно определяться правилом ЛЕВОСТОРОННЕГО БУРАВЧИКА:
Для γ + (м) кванта:
Если смотреть на удаляющийся от стороннего наблюдателя по проводнику γ + (эл) квант, по направлению в нём электрического поля, то движение γ +(м) по концентрической линии магнитной индукции (кольцевому Л.П.к. или Э.У.к.) вокруг прямолинейного проводника должно осуществляться против часовой стрелки, а движение γ ‾ (м) по "своим" кольцевым Л.П.к.(Э.У.к.) − тоже концентрической линии магнитной индукции, по часовой.
Для γ ‾(м) кванта:
Если смотреть на удаляющийся от стороннего наблюдателя по проводнику γ ‾(эл) квант, в направлении против имеющегося в нём электрического поля, то движение γ ‾(м) по концентрической линии магнитной индукции (кольцевому Л.П.к. или Э.У.к.) вокруг прямолинейного проводника должно осуществляться против часовой стрелки, а движение γ + (м) по "своим" кольцевым Л.П.к. (Э.У.к.) − концентрическим линиям магнитной индукции наоборот, по часовой стрелке (см. рис. 13).

Данные правила, "позволяют" как и прежде, пользоваться правилом правостороннего буравчика при определении направления вектора магнитной индукции (В) для прямолинейного тока.
11. Антиподно − эквивалентные, математические ряды ЭМРN в ряде ЭМР(− ∞ ÷ ∞ ), относительно оси "квадратов" располагаются в условных плоскостях, перпендикулярных ей и в процессе своего "перемещения" вдоль неё, постоянно сохраняют эту ориентацию в Пространстве. В соответствии с принципом Единства и Подобия, это положение относится как к различным Фликкер выбросам, так и различным материальным образованиям, являющимся по своей природе антиподно − эквивалентным.


Методические рекомендации:
По завершении прочтения представленного выше материала по теме "ПРЕДПОСЫЛКИ АНТИПОДНО − ЭКВИВАЛЕНТНОГО ПОДХОДА К ЭЛЕКТРОМАГНИТНЫМ ЯВЛЕНИЯМ" далее будут разобраны различные примеры по электромагнетизму. Но прежде чем Читатель приступит к их рассмотрению, ему предварительно (обязательно) следует ознакомиться со статьёй "Новый подход к объяснению опытов по электромагнетизму" авт. Лавров М.А. в журнале Самиздат. В ней, с позиции вышеприведённой методики, даётся объяснение следующих опытов:
1. Магнитная стрелка в однородном магнитном поле.
2. Действие магнитного поля на прямолинейный ток.
3. Опыт Г.Х. Эрстеда от 1820 года.
4. Взаимодействие прямолинейных токов.
5. Действие магнитного поля на движущийся заряд.
6. Разделение магнитным полем электрических зарядов.
7. Э.Д.С. индукции в движущихся проводниках.
8. Движение электрических зарядов в стороннем электрическом поле.
9. Взаимодействие одноимённых и разноимённых электрических зарядов.
10. Внутреннее устройство электрона и позитрона.


Примечание:
Эти и приводимые в данной статье примеры анализировались с обязательным учётом структуры магнитного поля электрона и позитрона, устройство которой предопределяет наличие в ней двух составляющих, и меридиональной, и экваториальной. Первая ориентирована вдоль их оси вращения, вторая, перпендикулярно ей. По отдельности, они схематично показаны на рисунках 27.1; 27.2 и 27.3 в п.10

указанной статьи. Эта конструктивная особенность учитывалась при прорисовке схематичных рисунков. В тех случаях, когда речь шла о меридиональной составляющей, на рисунке не прорисовывалась экваториальная составляющая магнитного поля электрона или позитрона, и наоборот; то же относится и к Л.П.эл. − линий напряжённости электрического поля электрона. Это позволило упростить прорисовку той или иной схемы. Подобную особенность обязательно следует учитывать Читателю, когда он в процессе прочтения статьи обращается к тому или иному схематичному рисунку. Последующая ссылка на статью в журнале "Самиздат" будет указываться цифрой 1 в скобках, т.е. (1).

3. Электрический диполь в однородном электрическом поле.

Из практики известно, что жёсткий электрический диполь в однородном электрическом поле стремится повернуться так, чтобы вектор его дипольного момента Ре был направлен параллельно вектору напряжённости поля Е (см. рис. 32). Объяснения такого поведения диполя в электрическом поле с причинных позиций ни в одном учебнике нет. Даётся лишь ссылка на электрические силы, заставляющие диполь принять такую ориентацию.




Вот теперь, зная в первом приближении причинную сторону взаимодействия как самих зарядов, так и поведение их во внешнем электрическом поле (см. п. 8 ÷ 9 в (1)), можно схематично, с причинных позиций объяснить поворот диполя в однородном электрическом поле.
В функциональной схеме взаимодействия диполя с электрическим полем следует выделить два этапа или два положения диполя в электрическом поле. Первое, когда вектор его дипольного момента располагается под углом к вектору напряжённости электрического поля Е или направлению его потоков γ + (эл) и γ ‾(эл) и сами электрические заряды не экранируют друг друга от этих потоков (см. рис. 33).
При таком положении, каждый из зарядов диполя по отдельности подвержен действию реактивных усилий, возникающих в их Л.П.эл. вследствие "перехода" квантов с Л.П.эл. внешнего электрического поля на Л.П.эл. электрического поля самих зарядов (или же е− −ов). На этом этапе заряды движутся в электрическом поле преимущественно по его направлению (условно).
Но подобное перемещение ограничено электрической связью между зарядами по линии Л.П.эл. в срединной области. А наличие этого фактора приводит к возникновению момента, который и разворачивает диполь по полю. В процессе разворота, силовая картина реактивных усилий в диполе по отношению зарядов меняется. С некоторого момента поворота заряды начинают всё больше и больше экранировать друг друга от потоков γ + (эл) и γ ‾(эл) электрического поля.
При достижении положения, когда вектор дипольного электрического момента Ре расположится вдоль направления вектора напряжённости электрического поля, положительный заряд окажется под преимущественным воздействием только потока γ ‾(эл), а отрицательный − под преимущественным воздействием только потока γ + (эл) (см. условный рис. 34).




При таком конечном положении, силовое воздействие на заряды со стороны электрического поля будет приходиться в основном на периферийные области (зоны) зарядов и они, по принципу разобранных функциональных схем рисунков 25; 26; 27 /см. в (1)/,

будут электрическим полем оттягиваться друг от друга. Максимальное расхождение зарядов будет определяться условием равенства суммарных реактивных сил в периферийных и срединной областях. При нарушении этого равенства, когда периферийные усилия превысят таковые в срединной области, электрическая связь между зарядами в срединной области нарушится и они удалятся друг от друга на " ∞ " −ое расстояние.

Пояснение к функциональной схеме рисунка 34.
Как и в предыдущих функциональных схемах "чисто" электрического характера /см. в (1)/, исходя из наглядности "перехода" квантов с Л.П.эл. одного электрического заряда на Л.П.эл. другого, т. е. из одного электрического поля в другое, данная функциональная схема выполнена разной цветовой гаммой. Этим самым более конкретно выделяются зоны преимущественного обменного взаимодействия каждых квантов.
Саму же схему условно можно представить как сочетание 2 −х функциональных схем − внутренней и внешней. Первая − это взаимодействие электрических полей разноимённых зарядов/см. рис. 26 в (1)/.

Вторая − это функциональная схема взаимодействия первой с внешним электрическим полем − см. рис.34. События, происходящие в этой схеме, "происходят" на фоне взаимодействий во внутренней. При этом обязательно следует учитывать ориентацию вектора дипольного электрического момента по отношению вектора напряжённости внешнего электрического поля.
При такой ориентации, когда вектор Ре параллелен вектору Е, осуществляется максимальное экранирование зарядов от потоков антиподных квантов внешнего электрического поля со стороны периферийных областей каждого заряда.
Для отрицательного − это зона П (см. рис.34). В ней γ + (эл) (оранжевый цвет) взаимодействует с Л.П.эл. (зелёный цвет). Соответственно суммарное реактивное усилие от этих Л.П.эл. передаётся отрицательному заряду и он потоком γ + (эл) (оранжевый цвет) оттаскивается вправо (в плане рисунка) от положительного заряда.
Для положительного заряда − это зона 1 (см. рис. 34). В ней, подобное действие, как и в случае с γ + (эл) (оранжевый цвет) , оказывают на Л.П.эл. (синий цвет) γ ‾(эл) (сиреневый цвет) из потока внешнего электрического поля. Возникающие суммарные реактивные усилия в этой зоне, через посредство Л.П.эл. (синий цвет), передаются положительному заряду. В результате он смещается влево (в плане рисунка), т. е. оттягивается от отрицательного заряда.
Когда растягивающие суммарные реактивные усилия от антиподных потоков квантов из внешнего электрического поля, во внешней (условно) функциональной схеме, сравняются с суммарными реактивными силами во внутренней, произойдёт нейтрализация последних. В последующем, по мере роста плотности антиподных потоков квантов внешнего электрического поля, растягивающие усилия в периферийных зонах обоих зарядов всё больше и больше будут "оттягивать" заряды друг от друга, удаляя их (условно) на " ∞ " −ое расстояние.

4. Отклонение движущихся заряженных частиц электрическим полем.

До этого момента, мы рассматривали взаимодействие положительных и отрицательных зарядов с внешним электрическим полем, исходя из условия, что они движутся в нём по его направлению.





При таком движении заряды не испытывают перемещений в перпендикулярном направлении к своей траектории (или вектору скорости).
Совсем по иному ведут себя заряженные частицы, когда внешнее электрическое поле перпендикулярно направлению скорости частицы. Влетая в такое электрическое поле, частица начинает испытывать ускорение в направлении перпендикулярном своему движению.
В учебниках, о причине такого ускорения ничего не говорится. Просто констатируется очевидность факта отклонения и даётся лишь математический аппарат определения расстояния по отклонению частицы от её первоначальной траектории. Из учебника И.В. Савельева "Курс общей физики" т.2 (Электричество и магнетизм. Волны. Оптика.), изд. "Наука", М., 1978г., приводится уловная схема такого отклонения

Подобный способ преподнесения учащимся учебного материала по данной тематике, по своей сути является описательным, без раскрытия истинной причины (механизма) отклонения заряженных частиц электрическим полем (тоже можно сказать и в отношении магнитного поля).
В связи со сказанным, вполне очевиден следующий вопрос: "Можно ли причинно объяснить (в первом приближении) природу возникновения перпендикулярного ускорения е− −на (е+ −на) в момент пролёта его (их) между обкладками конденсатора?"

Ответ: Можно.
Для ответа на этот вопрос обратимся к рисункам 21 и 22 /см. в (1)/. Повернём их в плоскости рисунка на 90° с обязательным указанием направления скорости частиц относительно направления внешнего электрического поля. В результате получим следующие, условно упрощённые функциональные схемы взаимодействия е− −на (е+ −на) с электрическим полем конденсатора (см. рис. 36 и 37).








В процессе преодоления зоны действия электрического поля конденсатора, как и в рассмотренных выше примерах чисто электрического характера (см. в (1)), γ + (эл) и γ ‾(эл) из внешнего электрического поля подвергают около электронное пространство позонному каналированию.
В е− −не для потока γ ‾(эл) таковой является зона 1, располагающейся (условно) выше линии О − О (см. рис.36). Для потока γ + (эл) − зона П.
Исходя из условия, что γ + (эл) и γ ‾(эл) взаимодействуют только со "своими" Л.П.эл. в данных зонах е− −на, будем иметь следующую направленность процессов в этих зонах:
γ ‾(эл) (синий цвет), переходя в зоне 1 с Л.П.эл. внешнего электрического поля (это поле между обкладками конденсатора) на Л.П.эл. е− −на (синий цвет), после передачи им реактивного импульса (усилия), будут двигаться вдоль этих Л.П.эл. от е− −на в направлении отрицательно заряженной пластины конденсатора. Соответственно суммарный реактивный импульс от всех "синих" Л.П.эл. в зоне 1 будет направлен наоборот, в направлении к положительно заряженной пластины.
γ + (эл) (красный цвет) в зоне П е− −на, тоже взаимодействуют со "своими" Л.П.эл. (красный цвет) и затем движутся вдоль них в том же направлении, что и γ ‾(эл) в зоне 1 (см. рис.36). Суммарный реактивный импульс от этих Л.П.эл. (красный цвет) по направлению будет совпадать с таковым от γ ‾(эл) в зоне 1 и тоже через их посредство "тянуть" е− −он в направлении к положительно заряженной пластины.

Отметим, что как и в предыдущих функциональных схемах электрического характера, рассмотренных выше − см. в (1), и в этих двух (см. рис.36 и 37)

передача импульсов "своим" Л.П.эл. квантами "осуществляется" позонно, по принципу позонной экранизации.
Такое, антиподно − эквивалентное объяснение движения е− −на во внешнем электрическом поле, перпендикулярно направленным вектору его скорости, "исключает" наличие у него абстрактного отрицательного заряда. В принципе, он и не нужен, ибо "отрицательность" е− −на в функциональной схеме рис. 36 определяется структурой его собственного электрического поля (в виде разнонаправленных Л.П.эл.) и избирательной направленностью происходящих в ней процессов.
Подобное происходит и с е+ −ом (пр. Е и П −ия!) − см. рис.37. Но в отличии от функциональной схемы е− −на, суммарные реактивные импульсы от соответствующих Л.П.эл. направлены не от отрицательно заряженной пластины конденсатора, а наоборот − от положительной, к отрицательной. Это и является причиной того, что е+ −он при пролёте между пластинами конденсатора смещается в направлении к отрицательно заряженной пластине.
После же вылета из зоны действия электрического поля конденсатора, внешнее электрическое поле отсутствует и обе частицы движутся в пространстве по прямолинейной траектории.

А теперь дадим итоговый результат по функциональным схемам взаимодействия электрических зарядов между собой и с внешним электрическим полем.
Всем электрическим схемам, рассмотренным выше − с учётом в (1), свойственна одна общая особенность, которую можно определить как эффект зональной экранизации. Необходимость его присутствия в этих функциональных схемах покажем на примере взаимодействия того же е− −на с внешним электрическим полем.
Считается, что при отсутствии внешнего электрического поля, все свободные в проводнике е− −ны пребывают в хаотическом движении, с произвольной ориентацией своих осей вращения. Но в момент подключения проводника к источнику питания, электрическое поле в виде двух взаимно встречных потоков γ + (эл) и γ ‾(эл) начинает распространяться по нему со скоростью света и первое, что оно сделает с е− −ми, из произвольной их ориентации переведёт в упорядоченную. Их Северный магнитный полюс повернётся в сторону потока γ + (эл), а Южный − в сторону потока γ ‾(эл). С учётом принципа Единства и Подобия, е− −он во взаимно встречных потоках антиподных квантов и в магнитном, и электрическом полях ведут себя одинаково /см. условный рис. 1 и 4 в (1)/.


После прихода е− −ов в упорядоченную ориентацию по отношению электрического поля, половина Л.П.эл. их электрических полей, ориентированная в направлении встречного потока γ + (эл), будут находиться под воздействием только этого потока. А остальная половина Л.П.эл., ориентированная в направлении попутного потока γ ‾(эл) − только под его воздействием.
Функциональная схема такого взаимодействия рассмотрена в (1) и "работает" по принципу "тяни − толкай". Для е− −на, "тянущим" потоком является встречный поток γ + (эл), а "толкающим" − попутный поток γ ‾(эл).
Взаимодействие γ + (эл) и γ ‾(эл) со "своими" Л.П.эл. из электрического поля электрона осуществляется зонально. Так Л.П.эл., в зоне справа от е− −на /см. рис. 21 в (1)/),

взаимодействуют только с γ + (эл) из встречного потока γ + (эл) и одновременно не пропускают их в зону электрических Л.П.эл. слева от е− −на (в плане рисунка). Одновременно Л.П.эл. электрического поля слева от него, взаимодействуют только с γ ‾(эл) из попутного потока γ ‾(эл), но также не пропускают их в зону Л.П.эл. справа от него.
Подобный вид зонального взаимодействия Л.П.эл. с γ + (эл) и γ ‾(эл) следует рассматривать как эффект зональной экранизации. Во всех рассмотренных выше примерах электрического характера − с учётом в (1), этот эффект имеет место.


5. Взаимодействие магнитных полей, подобных магнитному полю полосового
постоянного магнита.

В этой части статьи мы рассмотрим условно − упрощённые функциональные схемы взаимодействия магнитных полей, присущих постоянным магнитам, как−то магнитным стрелкам и однослойным соленоидам.
По современным представлениям структура их магнитных полей представляет однонаправленные линии магнитной индукции. По представлениям на сегодняшний момент времени, это воображаемые линии, выходящие из Северного магнитного полюса магнита и заходящие в противоположный, их Южный полюс (см. схематичный рис. 38). На обеих схемах этого рисунка они изображены в виде штрих пунктирных линий.





Из практики известно, что одноимённые магнитные полюса полосовых постоянных магнитов отталкиваются, а разноимённые − притягиваются.
Подчеркнём, что объяснение с причинных позиций взаимодействия подобных магнитных полей ни в одном учебнике по физике нет. И тем более нет соответствующей функциональной схемы подобного взаимодействия. Просто констатируется очевидность данного факта.

Так как данная статья имеет своей целью причинно объяснить (в первом приближении) физическую природу взаимодействия электромагнитных полей, то подобное объяснение, как и в случае электрических полей и зарядов, мы осуществим на примере разбора процессов перехода γ + (м) и γ ‾(м) − квантов электромагнитного поля, с одних Л.П.м. одного магнитного поля, на Л.П.м. другого, в соответствующих схемах электромагнитного характера.
В принципе, исходя из рассмотренных выше функциональных схем взаимодействия электрических полей и зарядов, нам следует определить направление действия суммарных реактивных импульсов (усилий), которые через посредство Л.П.м. − линий магнитной индукции, воздействуют на е− −ны в магнитах полях, заставляя их, а следовательно, и сами магниты, перемещаться в пространстве в ту или иную сторону. Удобнее всего это сделать, разбив функциональные схемы (условно) на зоны и проанализировать направленность "перехода" в них квантов (фотонов) с одних Л.П.м. на другие по отдельности.

В подобных, условно − упрощённых функциональных схемах, которые будут рассмотрены ниже, можно (условно) выделить следующие обменные зоны (области):
Зона или область 1.
Эту зону (см. например, рис. 39) по профилю исходящих из магнитных полюсов магнитов и одновременно заходящих в них Л.П.м., можно (условно) определить как "воронкообразная".
Зона П.
Эта зона граничит с зоной (областью) 1 и распространяется от неё по обе стороны и "сверху", и "снизу" (в плане рисунка). Зона П на плоскости занимает часть пространства между штрих − пунктирными линиями О1 − О1 и О2 − О2. При пространственном рассмотрении подобных функциональных схем, зона П охватывает область 1. Зону П условно можно интерпретировать как переходная, между зонами 1 и Ш.
3. Зона Ш.
Эта зона располагается за зоной П и в пространстве охватывает её. И если зону П можно считать (условно) промежуточной, то зону Ш периферийной. В ней, из окружающего магниты пространства, магнитные силовые линии или Л.П.м. − линии магнитной индукции, меридионально подходят от противоположных магнитных полюсов и переходят в зону П. Одновременно из зоны П в зону Ш выходят Л.П.м. противоположного направления и изгибаясь, удаляются в меридиональном направлении к противоположным полюсам магнитов.
Переход или обмен квантами между меридиональными Л.П.м. в этих зонах, осуществляется по преимущественному принципу в случае взаимодействия одноимённых магнитных полюсов. При разноимённых, обмен происходит и γ + (м), и γ ‾(м). Как это происходит, мы рассмотрим ниже, на примере взаимодействия магнитных полей полосовых постоянных магнитов или тех же магнитных стрелок (пр. Е и П −ия!).

5.1. Взаимодействие Южных магнитных полюсов.

Зона (область) 1 (см. условный рис. 39).


В ней обмен квантами идёт преимущественно по линии γ + (м). Так γ + (м) − (красный цвет) с Л.П.м. (красный цвет), исходящих из Южного магнитного полюса левого (в плане рисунка) магнита, "переходят" на Л.П.м. (зелёный цвет), исходящие из Южного магнитного полюса противоположного или правого (в плане рисунка) магнита.
После "перехода", γ + (м) (красный цвет) движутся вдоль "зелёных" Л.П.м. влево, в направлении левого (в плане рисунка) магнита. Одновременно γ + (м) − (зелёный цвет) "переходят" с "зелёных" Л.П.м. на Л.П.м. (красный цвет) и движутся вдоль них в направлении правого магнита (в плане рисунка).
Соответственно, суммарный реактивный импульс от γ + (м) − (зелёный цвет) направлен в сторону левого (в плане рисунка) магнита и через посредство его "красных" Л.П.м. и далее, находящихся в нём е− −ов, "толкает" левый магнит влево, удаляя его от правого. Но одновременно тоже происходит и с суммарным реактивным импульсом в отношении "зелёных" Л.П.м. правого магнита от квантов γ + (м) − (красный цвет). Этот реактивный импульс направлен в сторону правого (в плане рисунка) магнита и также, через посредство "зелёных" Л.П.м., "толкает" его в направлении от левого (в плане рисунка правого) магнита. Совместное действие суммарных реактивных импульсов от квантов γ + (м) левого и правого магнитов, через посредство Л.П.м. и далее е− −ов, направлено на их отталкивание.

Особо следует отметить характер поведения γ + (м) в процессе "выполнения" ими функции обмена. После "перехода" квантов γ + (м) от Л.П.м.. из одного магнитного поля, на подобные, но принадлежащие другому, они, двигаясь вдоль них, становятся "равноправными" по отношению пребывающих на этих Л.П.м. γ + (м). Но став таковыми, они теперь должны покинуть эти Л.П.м. и "перепрыгнуть" на ранее, ими оставленные. С них они снова повторят переход из одного магнитного поля в другое, находящимся с первым в суперпозиции.
Образно получается, что при суперпозиции магнитных полей, их составляющие, т. е. Л.П.м., постоянно обмениваются ("перебрасываются") квантами γ + (м) и тем самым как бы "обеспечивают" себя постоянными реактивными импульсами, которые они в "воронкообразной" области получают от γ + (м), что в конечном итоге и приводит к отталкиванию магнитов друг от друга.

2. Зона Ш − периферийная зона.
В этой зоне, так же как и в зоне (области) 1, идёт преимущественный обмен (переброс), но уже не γ + (м), а преимущественно γ ‾(м). В обмене участвуют Л.П.м. "синего" и "чёрного" цвета. По этим Л.П.м. γ ‾(м) перемещаются в направлении промежуточной зоны (зоны П). Но до неё если и доходят, то в очень ограниченном количестве (предположение). Они как бы "застревают" в периферийной зоне и активно участвуют в обеспечении Л.П.м. "синего" и "чёрного" цвета реактивными импульсами.
Направление суммарного реактивного импульса от γ ‾(м) (чёрный цвет) совпадает по направлению с таковым от γ + (м) (зелёный цвет) в воронкообразной зоне (зона 1), а от γ −(синий цвет) − в ней же от γ + (м) − (красный цвет). То есть и периферийная зона "функционирует" в преимущественном режиме отталкивания магнитов, так же как и зона (область) 1.
"Действуя" совместно, зона 1 и зона Ш и "определяют" характер взаимодействия постоянных полосовых магнитов, обращённых друг к другу одноимёнными (в данном случае Южными) магнитными полюсами.
BR>
3. Зона П − переходная или промежуточная зона.
В ней особо следует отметить совместное движение γ + (м) и γ ‾(м) вдоль соответствующих Л.П.м. перпендикулярно по направлению (конечно условно) к оси О − О. Так γ + (красный цвет), а также γ + (м) − (зелёный цвет), движутся по или вдоль "своих" Л.П.м. в одном направлении. Но в соответствии со схемой взаимодействия прямолинейных проводников /см. рис. 11; 9; 12 в (1)/ с одно направленными токами, подобное движение квантов, как и в случае движения е− −ов по проводнику, предопределяет притяжение этих Л.П.м. (пр. Е и П −ия!).

Одновременно, но уже по "своим" Л.П.м. "синего" и "чёрного" цвета, осуществляется однонаправленное движение и γ ‾(м). Следовательно, и эти Л.П.м., по идее тоже должны притягиваться друг к другу (пр. Е и П−ия!).

В тоже время, при наличии суперпозиции магнитных полей в зоне П следует отметить, что относительно друг друга, γ + (м) и γ ‾(м) по "своим" Л.П.м. движутся во взаимно встречном направлении. Но тогда, в соответствии со схемой взаимодействия прямолинейных проводников с разнонаправленными токами /см. рис. 11; 9; 12 в (1)/, Л.П.м. с разнонаправленным движением по или вдоль них квантов, как и в случае с е− −ми, должны отталкиваться друг от друга.
То есть, исходя из функциональных схем взаимодействия прямолинейных проводников с токами − (пр. Е и П −ия!), в зоне П часть Л.П.м. одновременно должны как отталкиваться друг от друга, так и одновременно притягиваться. Подобное, исходя из принципа Единства и Подобия, должно иметь место и в случае отдельно взятого магнитного поля, например, того же однослойного соленоида или катушки с током. Но такое возможно только при наличии разнонаправленных Л.П.м. в структуре магнитного поля.
При наличии разнонаправленных Л.П.м., в пространстве вокруг соленоида и взаимно встречного движения по ним γ + (м) и γ ‾(м), в подобных магнитных полях, Л.П.м. должны одновременно притягиваться и отталкиваться, располагаясь на определённом расстоянии друг от друга. Это происходит, когда силы отталкивания Л.П.м. и силы их притяжения уравновешиваются.
Но вот здесь, со всей очевидностью правомерен следующий вопрос: "В проводниках, при наличии электротока, в качестве взаимодействующих сторон выступают е− −ны и кванты электромагнитного поля, а в Л.П.м.?" Ясно, что по отношению к ним, одной взаимодействующей стороной являются антиподные кванты или кванты электромагнитного поля, или же фотоны света. А что же по отношению их "выполняет" роль Фликкер выброса?

Если исходить из принципа Единства и Подобия, то эти материальные образования в − " ∞ " −ти (по своим размерам они должны быть намного меньше фотонов − квантов электромагнитного поля, и функциональное состояние, в котором они пребывают в Л.П.м., должно быть не иначе как состояние "квадрата"), в самих Л.П.м. подобны квантам электромагнитного поля в проводниках. В функциональном отношении эти образования должны взаимодействовать с γ + (м) и γ ‾(м) всё по той же функциональной схеме взаимодействия прямолинейных проводников с токами, что и е− −ны. Этого "требует" пр. Е и П −ия! Но тогда и сами γ + (м) и γ ‾(м) или фотоны света, по своему внутреннему и функциональному устройству, должны быть подобны е− −ам (е + −ам). Этого также "требует" пр. Е и П −ия!

Рассуждая подобным образом, приходишь к мысли, что в Л.П.м., подобно проводникам, тоже циркулируют соответствующие токи и одной из компонент таких токов являются кванты электромагнитного поля. Но тогда, исходя опять же из пр. Е и П −ия, получается, что внутреннее устройство квантов электромагнитного поля должно быть подобно внутренней и внешней структуре е− −ов (е+ −ов). То есть в окружающем фотоны пространстве должны быть не только соответствующие меридиональные и кольцевые − экваториальные линии "магнитной" индукции, но также и Л.П.эл. соответствующего "электрического" поля. Только при наличии таковых и соответствующих Фликкер выбросов в самих Л.П.м, "обеспечивающих" взаимодействие γ + (м) и γ ‾(м) − квантов электромагнитного поля, и возможно как отталкивание, так притяжение линий "магнитной" индукции в магнитных полях. С полным основанием, сказанное можно отнести и к электрическим Л.П.эл. − пр. Е и П −ия!
Не будь этого, при наличии из − в + " ∞ " −ть в окружающем нас Мире только однонаправленных Л.П. ( да в тех же магнитных и электрических полях), они бы, исходя из функциональной схемы взаимодействия прямолинейных проводников с однонаправленным током, просто притянулись бы друг к другу и (образно) стянулись бы в " ∞ " −но "тонкую" линию. Но ведь этого в Природе нет! Значит что −то препятствует их такому слиянию? (! . . .).

5.2. Взаимодействие Северных магнитных полюсов.

1. Зона (область) 1 (см. условный рис.40).
В этой зоне обмен между Л.П.м. преимущественно осуществляется γ ‾(м). При этом только теми Л.П.м., которые выходят из магнитных полюсов. Так от "синих" Л.П.м., γ ‾(м) − (синий цвет) от левого (в плане рисунка) магнита, "переходят" на участки "черных" Л.П.м, выходящими из Северного магнитного полюса правого (в плане рисунка) магнита.
После перехода, они движутся вдоль этих участков "чёрных" Л.П.м. влево (в плане рисунка), в сторону левого магнита. А суммарный реактивный импульс от них, через посредство "чёрных" Л.П.м. передаётся е− −ам правого магнита, а от них и ему, вынуждая его отодвигаться от левого (в плане рисунка) магнита вправо.
Одновременно γ ‾(м) − (чёрный цвет) "переходят" на "синие" Л.П.м., выходящие из Северного магнитного полюса левого (в плане рисунка) магнита и затем движутся вдоль них в направлении правого. Суммарный реактивный импульс, полученный "синими" Л.П.м. от γ ‾(м) − (чёрный цвет), через посредство этих Л.П.м. также передаётся е− −ам, но уже левого магнита, а через них и ему самому.



Совместное действие суммарных реактивных импульсов от γ ‾(м) в "воронкообразной" зоне (области) на "синие" и "чёрные" Л.П.м. направлено на отталкивание магнитов, обращённых друг к другу одноимёнными, Северными магнитными полюсами.

2. Зона Ш − периферийная зона.
В этой зоне обмен между Л.П.м. преимущественно осуществляется γ + (м). В обмене в основном "участвуют" только те Л.П.м., которые меридионально "заходят" в зону Ш и далее, чрез неё в зону П. Это Л.П.м. красного и зелёного цвета (см. рис.40).
Так например, γ + (м) − (красный цвет) с "красных" Л.П.м. "переходят" на "зелёные" Л.П.м., а γ + (м) − (зелёный цвет) с "зелёных" Л.П.м. на "красные". Соответственно, суммарные реактивные импульсы от квантов γ + (м) в этой зоне, будут направлены в противоположные стороны их движения вдоль соответствующих Л.П.м. По "красным" Л.П.м. γ + (м) − (зелёный цвет) − движутся вправо (в плане рисунка), следовательно, суммарный реактивный импульс от них будет направлен вдоль "красных" Л.П.м. влево. А для "зелёных" Л.П.м., от γ + (м) − (красный цвет) вправо.
Совместное действие суммарных реактивных импульсов от γ + (м) и γ ‾(м) в зонах 1 и Ш направлено на отталкивание магнитов друг от друга.

3. Зона П − переходная или промежуточная.
Эта зона, по характеру происходящих в ней процессов, подобна зоне П в выше рассмотренной функциональной схеме взаимодействия полосовых постоянных магнитов, обращённых друг к другу Южными магнитными полюсами. Смотри соответствующие пояснения к ней.

5.3. Взаимодействие разноимённых полюсов постоянных полосовых магнитов.

В этой функциональной схеме (см. рис. 41), так же как и в подобных предыдущих функциональных схемах, выделим зоны преимущественной передачи реактивных импульсов: "воронкообразную" в районе магнитных полюсов; промежуточную или переходную, где по условному допущению (с нашей стороны) кванты движутся в пространстве вдоль своих Л.П.м. перпендикулярно оси О − О и периферийную − зону Ш по обе стороны от осей О2 − О2.
Отметим следующие обменные процессы перехода квантов по зонам:
1. Зона (область) 1 (см. условный рис.41).
В ней, γ + (м) − (красный цвет) с "красных" Л.П.м., выходящих из Южного магнитного полюса правого (в плане рисунка) магнита, "переходят" на "зелёные" Л.П.м., заходящие в воронкообразной области в Северный магнитный полюс левого (в плане рисунка) магнита.
Суммарный реактивный импульс от γ + (м) − (красный цвет), через посредство "зелёных" Л.П.м. передаются е− −ам левого (в плане рисунка) магнита, а от них и ему. Это "заставляет" левый магнит смещаться (в плане рисунка) слева − направо, в сторону правого магнита.




Одновременно с γ + (м), подобный переход осуществляют и γ ‾(м) − (чёрный цвет) "чёрных" Л.П.м., выходящих из Северного магнитного полюса левого (в плане рисунка) магнита, на "синие" Л.П.м., заходящие в воронкообразной области в Южный магнитный полюс правого магнита. Суммарный реактивный импульс от этих γ ‾(м) квантов, через посредство "синих" Л.П.м. передаётся е− −ам правого (в плане рисунка) магнита, что приводит его в движение в направлении левого.
В итоге, в результате перехода (переброса) антиподных квантов ( γ + ; γ −) с одних Л.П.м. на другие, в воронкообразной области создаются условия для постоянного действия суммарных реактивных сил в отношении соответствующих Л.П.м. и, как следствие, зона 1 "функционирует" в режиме притяжения разноимённых полюсов или просто магнитов.

2. Зона Ш − периферийная зона.
Если в зоне (области) 1 "переход" квантов осуществлялся с участков Л.П.м., выходящих из магнитных полюсов магнитов, на участки Л.П.м. , заходящие в магнитные полюса, то в зоне Ш имеет место несколько иная направленность перехода квантов. В ней, переход квантов идёт с участков Л.П.м., заходящих в зону Ш, на участки Л.П.м. , выходящие из неё.
Так например, γ + (м) − (зелёный цвет) с "зелёных" Л.П.м. от левого (в плане рисунка) магнита "переходят" на "красные" Л.П.м, "выходящие" из зоны П в зону Ш. После перехода, они движутся по или вдоль них в направлении к Южному полюсу правого магнита. Суммарный реактивный импульс от этих, "красных" Л.П.м., передаётся е− −ам правого (в плане рисунка) магнита в направлении левого, заставляя правый смещаться в сторону левого.
Одновременно, в зоне Ш идёт "переход" γ ‾(м). Они с "синих" Л.П.м., заходящих в эту зону, "переходят" на "чёрные" Л.П.м. выходящие из этой зоны. После перехода они движутся по или вдоль них в направлении к Северному магнитному полюсу левого (в плане рисунка) магнита, т. е. в направлении от правого. Суммарный реактивный импульс от γ ‾(м) − (синий цвет), через посредство "чёрных" Л.П.м. магнитного поля левого (в плане рисунка) магнита, передаётся в нём е− −ам, заставляя левый магнит смещаться в сторону правого.
В итоге, совместное действие суммарных реактивных импульсов от γ + (м) и γ ‾(м) в зоне Ш направлено так же как и в зоне 1, на притяжение полосовых магнитов, обращённых друг к другу разноимёнными магнитными полюсами.

3. Зона П − переходная или промежуточная.
Соответствующие пояснения в отношении этой зоны смотри в предыдущих примерах.

Методические пояснения к функциональным схемам рисунков 39; 40 и 41.

Так как основным требованием, предъявляемым к функциональным схемам электромагнитного характера, является раскрытие (в первом приближении) причинного механизма взаимодействия как электрических, так и магнитных полей, то, исходя из этого требования, в их структуре были "выделены" элементы, способные "выполнять" функцию притяжения или отталкивания.
В качестве таковых в электрических полях являются Л.П.эл. − линии напряжённости электрического поля, в магнитных − линии магнитной индукции (тоже Л.П.м.). В качестве же посредников взаимодействия между Л.П. , в обоих случаях выступают соответствующие "представители" Фликкер выброса − кванты электромагнитного поля или соответствующие разновидности фотонов света.
Результат взаимодействия Л.П. − получение ими реактивных импульсов от γ + или γ ‾. В последующем эти импульсы через посредство Л.П. передаются е− −ам, а от них соответствующим материальным образованиям, в которых они пребывают.
Если в отношении магнитных полей брать именно такой "сценарий" в качестве их природного механизма притяжения или отталкивания, то, исходя из условий первого приближения, первостепенную роль в функциональном обмене следует отводить тем Л.П.м. в зонах суперпозиции, которые "работают" на конечный, правильный результат − притяжение или отталкивание.
Руководствуясь такой установкой при анализе взаимодействия магнитных полей полосовых постоянных магнитов, обращённых друг к другу, например, одноимёнными полюсами, в подобных функциональных схемах можно "выделить" зоны (области) преимущественного обмена между соответствующими Л.П.м. только одним видом квантов − или γ + (м), или γ ‾(м) − (см. рис. 39 и 40 и пояснения к ним).
В случае взаимодействия разноимённых магнитных полюсов, таких зон нет, ибо притяжение магнитов идёт за счёт обмена между соответствующими Л.П.м. одновременно обоими видами квантов. Так, в зоне (области) 1 (см. рис.41) обмен между Л.П.м. осуществляется одновременно как γ + (м), так и γ ‾(м) в направлении с выходящих из магнитных полюсов соответствующих Л.П.м., на соответствующие Л.П.м., заходящие в полюса противоположных магнитов (см. пояснение к рис.41).
Подобное можно отметить и в зоне Ш. Но в ней, в отличии от зоны (области) 1, одновременный обмен обоими видами квантов идёт в направлении с меридионально заходящих в зону Ш Л.П.м., на соответствующие Л.П.м. выходящие из неё.
При выделении именно такой направленности в деле функционального обмена квантами (рис. 41), зона Ш как и зона 1 как бы "работает" именно на притяжение полосовых постоянных магнитов, обращённых друг к другу разноимёнными магнитными полюсами.

В функциональной схеме рис. 41 "просматривается" отсутствие процесса "переброса" квантов между однотипными Л.П.м., которое "имеет" место в функциональных схемах рис.39 и 40. Если же при функциональном анализе схемы рис. 41 в зоне 1 учитывать и возвратный "переброс" (переход) γ + (м) − (красный цвет) с участков "зелёных" Л.П.м., заходящих в Северный магнитный полюс левого (в плане рисунка) магнита, на участки "красных" Л.П.м., выходящих из Южного магнитного полюса правого (в плане рисунка) магнита, и тоже делать в этой зоне в отношении "переброса" (перехода) γ ‾(м) − (чёрный цвет) с участков "синих" Л.П.м. на участки "чёрных" Л.П.м., то соответствующие участки "красных" и "чёрных" Л.П.м. в этой же зоне 1 "работали" бы на отталкивание магнитов. Этим самым нейтрализовалось бы действие участков тех Л.П.м., которые в зоне 1 "работают" на притяжение магнитов.
Подобную ситуацию можно "усмотреть" и в отношении γ + (м) − (зелёный цвет) и γ ‾(м) − (синий цвет) при переходе первых с участков "красных" Л.П.м. на участки "зелёных" и вторых, с участков "чёрных" Л.П.м. на участки "синих" в зоне Ш. Подобный возвратный "переброс" (переход) в этой зоне также нейтрализовал бы "работу" тех участков соответствующих Л.П.м., которые тоже вкупе с соответствующими участками Л.П.м. в зоне 1, "работают" на притяжение магнитов.
Но из опыта мы знаем, что подобного на практике не наблюдается. Полосовые постоянные магниты, с завидным усилием притягиваются друг к другу, когда взаимодействуют разноимёнными магнитными полюсами. А это даёт основание (в первом приближении) не учитывать или "отбросить" при функциональном анализе схемы рис. 41 возвратный "переброс" вышеназванных квантов и во внимание (пока что) брать только направленность в обменном взаимодействии между Л.П.м., которая направлена только на притяжение магнитов. Насколько правомерна именно такая точка зрения по данному вопросу, пока сказать трудно. А потому решение этого вопроса оставим на Будущее.

6. Сила Лоренца.

На электрический заряд, движущийся в магнитном поле, действует сила Лоренца, которая определённым образом искривляет его траекторию. Прежде чем мы перейдём к раскрытию причинной стороны её возникновения в структурной схеме электрического заряда, нам следует обратиться к условным схемам действия электрического и магнитного полей на электрический заряд.
На рис. 74 приводятся две условные схемы такого действия. На них оба поля действуют на отрицательный заряд (электрон) в одном направлении. Отличительной особенностью этих схем является то, что вектор напряжённости электрического поля Е и вектор магнитной индукции магнитного поля В, по отношению друг друга в пространстве располагаются под углом 90° . Проанализируем обе схемы с точки зрения действия квантов γ + и γ ‾ на соответствующие структурные области электрона.


В схеме, в которой показано движение е− −на между обкладками конденсатора (см. рис. 74а), фотоны или кванты из внешнего электрического поля − γ + (эл) и γ ‾(эл), взаимодействуя по выше описанной схеме с Л.П.эл. электрона, располагающиеся во внешней его области − иначе, вокруг его ядра, вынуждают электрон смещаться в направлении к "положительно" заряженной пластине (см. также рис. 36 и 37). В результате его траектория искривляется. Сила, смещающая электрон в электрическом поле, по направлению действия совпадает с направлением вектора напряжённости электрического поля Е.

Совсем иная картина имеет место в схеме взаимодействия электрона с магнитным полем (см. рис. 74б). Направление действия магнитной силы на него со стороны поля не совпадает с направлением вектора магнитной индукции В. Угол между ними составляет 90° . Вполне правомерен вопрос: "Как правильно объяснить подобное различие обеих схем и какие подструктуры е− −на участвуют во взаимодействии с электрическими γ + (эл); γ ‾(эл) и магнитными γ + (м); γ ‾(м) квантами?"

Ответ:
В случае с электрическим полем ясно. Таковыми являются Л.П.эл. электрона. Именно их взаимодействие с γ + (эл) и &gammа; ‾ (эл) квантами и вызывает смещение е− −на по направлению вектора напряжённости электрического поля Е.
Теперь допустим, что в случае магнитного поля действию со стороны γ + (м) и γ ‾(м) подвергаются те же Л.П.эл. электрона. Вопрос: "В каком направлении должен сместиться е− −он ?"

Ответ:
Так как подобная функциональная схема будет идентична схеме действия электрического поля на е− −он, то исходя из неё можно сказать, что он, пролетая сквозь однородное магнитное поле (с учётом, что вектор Е перпендикулярен вектору В на рис. 74а), сместится по направлению вектора магнитной индукции В, в сторону потока γ + (м). То есть направления, по которым сместится е− −он в электрическом и магнитом полях, будут относительно друг друга в пространстве взаимно перпендикулярны.
Но подобный (мысленный) результат по отношению схем рис. 74 противоречит опытному факту, ибо мы заведомо условились, что оба поля будут действовать на е− −он в одном направлении.
Вопрос: "На что "указывает" такое несоответствие мысленного и практического опытов?"
В данном случае ответ должен быть однозначным: кванты γ + (м) и γ ‾(м) из внешнего магнитного поля воздействуют на соответствующие подструктуры е− −на избирательно. Оставляют в покое Л.П.эл. и реактивно взаимодействуют со "своими" Л.П.м. (Э.У.к.). Вопрос: "Какими?"

Ответ: С целью выявления подобных Л.П.м. (Э.У.к.) обратимся к функциональной схеме рисунка 7а или 7б /см. в (1)/.

На них условно изображено сечение проводника и в нём условно показано направление электрического тока или направление движения квантов γ + (эл) и γ ‾(эл). Эти кванты, после прохождения внутренних областей е− −на, т. е. его осевого (диаметрального) О.Т., керна и экваториальных (диаметральных) О.Т. /см. рис. 27.1 и 27.2 в (1)/,

в конечном итоге оказываются на кольцевых Э.У.к., располагающихся в экваториальной его зоне. То есть в экваториальной составляющей магнитного поля е− −на − (примечание: у Земли, так же как и у электрона имеются свои Э.У.к. − это ничто иное как радиационные пояса планеты /пр. Е и П −ия!/. Таковых у неё два. Внутренний на высоте ~ 4000 км. Внешний на высоте ~ 17000 км. Первый открыт американским учёным Джеймсом ван Алленом, а второй советскими учёными С.Н. Верновым и А.Е. Чудаковым в 1958 г., см. в Интернете.)

В первом приближении мы исходим из того, что данные Э.У.к. появляются у электронов с начала движения по проводнику квантов γ + (эл) и γ ‾(эл) или с начала распространения вдоль проводника строннего электрического поля. Как только Э.У.к. возникают в около проводниковом пространстве, так тот час кванты γ + (м) и γ ‾(м) из внешнего магнитного поля начинают взаимодействовать с ними. От подобного взаимодействия Э.У.к. получают реактивные импульсы, которые затем "передаются" е− −ам, а от них и проводнику.
Так как данные импульсы, с учётом позонного эффекта, по обе стороны от оси проводника направлены в одну сторону, то совместное их действие на е− −ны, да и на сам проводник, обусловливает возникновение суммарной реактивной силы, которая в одном случае выталкивает проводник из магнитного поля /рис. 7а; в (1)/,

а в другом наоборот, втягивает /рис. 7б; в (1)/.
Из этих функциональных схем однозначно следует вывод, что суммарная реактивная сила, действующая на движущийся по проводнику е− −он (−ны), при наличии соответствующего внешнего магнитного поля, направлена перпендикулярно направлению его вектора магнитной индукции В и направлению скорости V е− −на (−ов).

А теперь вспомним, как действует на е− −он сила Лоренца в момент его пролёта сквозь внешнее, однородное магнитное поле. Согласно правила левой руки, её направление должно быть перпендикулярно вектору магнитной индукции В поля и вектору его скорости. То есть, что и в случае рисунков 7а и б, что и в случае правила левой руки, мы имеем один и тот же результат: и магнитное поле подковообразного магнита, через посредство своих квантов γ + (м) и γ ‾(м), и сила Лоренца, характеризующая действие внешнего магнитного поля на е− −он (на электрический заряд), действуют в одном направлении.
Учёт этого обстоятельства позволяет с позиции принципа Единства и Подобия сделать вывод: сила Лоренца, вызывающая смещение е− −на (е+ −на) или же "отрицательных" и "положительных" зарядов в том или ином направлении, обусловлена воздействием квантов γ + (м) и γ ‾(м) из внешнего магнитного поля на экваториальную составляющую магнитного поля е− −на (е+ −на). При этом следует особо отметить, что подобное действие будет только в том случае, когда у е− −на (−ов), тоже и у е+ −на (−ов), есть в наличии Э.У.к., т. е. когда они движутся в пространстве относительно внешнего магнитного поля и своими линиями магнитной индукции (Э.У.к.) пересекают линии магнитной индукции в самом поле.
Подобное пресечение сопровождается переходом квантов γ + (м) и γ ‾(м) с Л.П.м. внешнего магнитного поля − магнитного поля подковообразного магнита, на кольцевые Л.П.к. или кольцевые Э.У.к. электрона (−ов). В процессе такого перехода и возникают силы, которые суммируются в общую силу, названной в честь голландского физика Г.А. Лоренца.

Если же е− −он (е+ −он) неподвижны в пространстве, т. е. не перемещаются относительно магнитного поля, то оно на неподвижный заряд (е− −он, е+ −он) не в состоянии оказать какое−либо действие (примечание: не исключено, что Э.У.к у е− −ов присутствуют постоянно, но им свойствена прецессия относительно друг друга и внешнее магнитное поле действует на них только тогда, когда при движении е− − на они все группируются в одной, экваториальной его плоскости во время его движения в пространстве. То есть, когда они все сориентируются перпендикулярно вектору скорости электрона. Например, в солнечной системе подобная прецессия колец регулярно происходит у планеты Сатурн).

В чём же причина такого "безразличия" к неподвижному электрическому заряду со стороны магнитного поля?" Это "безразличие" может быть обусловлено двумя причинами, а вернее одной из них. Какая из них, сейчас сказать трудно и потому автор даст предположительную версию отсутствия взаимодействия однородного магнитного поля с неподвижным зарядом.

Версия 1.
У неподвижного е− −на (е+ −на) отсутствуют кольцевые Э.У.к. в экваториальной зоне. Это может быть только в том случае, если у него закрыты экваториальные О.Т. по случаю расперекрытия соответствующих проходных "окон" в сферических слоях внутри ядра е− −на (−ов). В соответствии с пр. Е и П −ия подобная ситуация может быть и у е+ −на, а также других, подобных им частиц. В этом отношении не являются исключением и планеты, звёзды, галактики, Вселенные и т. д., т. е. все подобные образования из − в + " ∞ " −ть (пр. Е и П −иия!) − (примечание: о наличии такого состояния экваториальных О.Т. − см. в (1) схематичный рис. 27.2,

речь будет идти при структурно − функциональном анализе ряда ЭМРN. Данный анализ ряда ЭМРN, а также ЭМР(− ∞ ÷ ∞) будет дан в последующем отдельной статьёй).
С началом движения е− −на (е+ −на) в пространстве, его экваториальные О.Т. переходят в открытый режим и вокруг него (них) тотчас возникают соответствующие Л.П. и меридионального, и экваториального направлений (Л.П.м. и Л.П.экв., т. е. Э.У.к.). При наличии Э.У.к. у подвижных е− −ов, внешнее магнитное поле в состоянии оказывать на него (следовательно и на проводник) действие, которое исторически ассоциируется с силой Лоренца.

Версия 2.
У подвижного и неподвижного е− −на (−ов) постоянно имеются в наличии не только Э.У.к., но и Л.П.м., т. е. меридиональная и экваториальная компоненты его (их) собственного магнитного поля присутствуют постоянно.
При таком варианте следует учитывать ориентацию е− −ов относительно друг друга в электрическом заряде. Не исключено, что они относительно друг друга ориентированы произвольно и тем самым создаются условия, когда отдельно взятые силы Лоренца от каждого е− −на компенсируют друг друга, а результат − суммарная сила Лоренца в таком электрическом заряде, подвергающемуся действию магнитного поля, будет равна нулю, что и отразится на поведении заряда в магнитном поле. Какова бы ни была его напряжённость, электрический заряд в нём будет оставаться неподвижным, т. е. суммарная сила Лоренца Э.У.к. всех е− −ов будет равна нулю.
Какая из этих версий реализуется в действительности, покажут будущие исследования по устройству е− −на (е+ −на) и т. д., а пока перейдём к рассмотрению вопроса о движении электрического заряда в магнитном поле.


6.1. Действие магнитного поля на движущийся заряд.

Прежде чем мы приступим к рассмотрению различных схем взаимодействия магнитного поля с электрическими зарядами, выясним поведение е− −на (е+ −на) в этом поле без конкретной, наглядной схемы. С этой целью обратимся к рисунку 7а; /см. в (1)/.

Раньше, при его анализе мы выяснили наличие соответствующих сил и их направленность с тем, чтобы их наличие в данной функциональной схеме определяло направление движения проводника с током под действием магнитного поля, которое является следствием взаимодействия квантов γ + (м) и γ ‾(м) магнитного поля с кольцевыми Э.У.к. электронов. Обращение к данной функциональной схеме обусловлено тем, что она отражает схематично то, что происходит в действительности. Попробуем перейти от этой конкретной схемы к общей, движению е− −ов (е+ −ов) в однородном магнитном поле.
Произведём (мысленно) в ней некоторые преобразования. Удалим из неё проводник и подковообразный полосовой магнит. Вместо них оставим (условно) только линии индукции магнитного поля и летящий сквозь это поле электрон. Всю схему развернём в плоскости рисунка против часовой стрелки на 90° . В результате подобных преобразований получим условную схему, которая представлена на рис. 13а в (1).



На этой функциональной схеме магнитное поле направлено "сверху" − "вниз" и своими квантами γ + (м) и γ ‾(м) реактивно воздействует на кольцевые Э.У.к . е− −на. Условно считаем, что е− −он удаляется от стороннего наблюдателя за плоскость чертежа. При этом вектор магнитной индукции В и вектор скорости е− −на Vе− взаимно перпендикулярны и лежат в одной плоскости, перпендикулярной плоскости чертежа. Более наглядно взаимное расположение векторов и действующих на е− −он сил в этой функциональной схеме видно на рисунке 13б /в (1)/, на котором рисунок дан в изометрической проекции − (примечание: на схеме отсутствует меридиональная составляющая магнитного поля электрона.)
В процессе движения е− −на сквозь магнитное поле, его кольцевые Э.У.к. пересекают линии магнитной индукции. Результатом такого пересечения является переход (перескакивание) квантов γ + (м) и γ ‾(м) с силовых линий магнитного поля на кольцевые линии Э.У.к. электрона.
С учётом позонного эффекта экранизации квантов γ + (м) и γ ‾(м) в соответствующих областях внешней структуры электрона, где располагаются Э.У.к., Л.П.м. и Л.П.эл. его магнитного и электрического полей, та полусферическая область, которая располагается выше горизонтальной линии О − О /см. рис. 13а в (1)/, подвержена действию только γ ‾(м) квантов, а которая под ней, только действию γ + (м) квантов.

Как было показано при анализе функциональной схемы рисунка 13а, соответствующие участки экваториальных Э.У.к. в этих полусферических областях, получают от квантов магнитного поля соответствующие реактивные импульсы. Эти импульсы "сверху" и "снизу" (в плане рисунка) от оси О − О позонно суммируются в одном направлении, что приводит к возникновению общей реактивной силы, которая и искривляет (отклоняет) траекторию полёта электрона в магнитном поле. Направление действия этой, суммарной силы перпендикулярно вектору магнитной индукции магнитного поля В и вектору скорости е− −на Vе−.
Одновременно с этим следует отметить, что воздействию γ + (м) и γ ‾(м) из внешнего магнитного поля подвержены не только кольцевые Э.У.к., т. е. экваториальная составляющая магнитного поля электрона, но и Л.П.м., и Л.П.эл. Они не "избегают" подобной участи.

Высказать какие−либо соображения по этому поводу, пока не представляется возможным. Ведь по идее и Л.П.м., и Л.П.эл. тоже должны находиться под воздействием этих квантов. Пока что, на данном этапе наших знаний о поведении электрона в магнитном поле, будем исходить из практических наблюдений, согласно которых сила, искривляющая его траекторию при пролёте сквозь магнитное поле, действует избирательно только на его экваториальные Э.У.к., т. е. на его экваториальную составляющую его собственного магнитного поля.

Функциональная схема рисунка 13б /см. в (1)/, на которой удаляющийся от стороннего наблюдателя электрон отклоняется вправо, исподволь "накладывает" соответствующие требования в отношении направления движения квантов γ + (м) и γ ‾(м) по кольцевым Э.У.к электрона, после того как они на них окажутся.
Чтобы данная схема соответствовала практике наблюдений, необходимо, чтобы кванты γ ‾(м) по "своим" Э.У.к. в электроне, по отношению стороннего наблюдателя, двигались в направлении против часовой стрелки, а кванты γ + (м) по "своим" − по часовой. При выполнении этих условий, электрон, через посредство экваториальных Э.У.к. и возникающих в них реактивных сил, будет в магнитном поле смещаться так, как показано на рисунке 13 в (1). Исторически, подобные реактивные силы во внешней структуре электрона принято называть в честь голландского физика Г.А. Лоренца (1853 - 1938).

В то же время, электрон в магнитном поле, перпендикулярным направлению его скорости, может отклоняться и влево по отношению стороннего наблюдателя. Это произойдёт в том случае /см. рис. 14а в (1)/,

если магнитное поле будет направлено не "сверху" − "вниз", а наоборот, "снизу" − "вверх". При такой ориентации кванты γ ‾(м) будут "атаковывать" свои кольцевые Э.У.к. "снизу", а γ + (м) свои "сверху". В результате сила Лоренца изменит своё направление и электрон по отношению стороннего наблюдателя, в таком магнитном поле отклонится влево. То есть летящий в пространстве электрон должен чутко реагировать на ориентацию внешнего магнитного поля, сквозь которое он пролетает.

А какое требование в отношении кольцевых Э.У.к должно соблюдаться в случае с позитроном, чтобы он при направлении магнитного поля "сверху" − "вниз" отклонялся влево по отношению стороннего наблюдателя? Какую ориентацию в пространстве он должен при этом соблюдать?

Об ориентации и е− −на, и е+ −на, которую они должны иметь при движении в пространстве, мы можем судить по тому, как они ориентируются при пролёте сквозь электрическое поле. Ведь с точки зрения принципа Единства и Подобия, во всех случаях, когда они движутся в пространстве, они должны ориентироваться одинаково.
Так е− −он, в электрическом поле движется навстречу потоку γ + (эл) (см. рис. 21 в (1) и пояснения к нему).

Следовательно, в направлении этого, встречного потока, он должен "смотреть" своим Северным магнитным полюсом, а попутного γ ‾(эл) − Южным. Для е+ −на должна быть противоположная ориентация. Следовательно, в направлении своего движения он должен "смотреть" своим Южным магнитным полюсом, а в направлении попутного потока γ + (м) − Северным.
Учёт этого обстоятельства позволит определить и обязательные требования в отношении его Э.У.к., т. е. экваториальной составляющей его магнитного поля, чтобы он при пролёте сквозь однородное магнитное поле, направленное "сверху" − "вниз", с точки зрения стороннего наблюдателя отклонялся влево. Это произойдёт, если реактивные импульсы от γ ‾(м) на соответствующих участках его Э.У.к. будут направлены слева − направо. Тоже требование предъявляется и к реактивным импульсам от γ + (м). То есть γ ‾(м) по "своим" Э.У.к. в экваториальной зоне е+ −на, с точки зрения стороннего наблюдателя должны двигаться по часовой стрелке, а γ + (м) по "своим" − против. При выполнении этих требований, он при пролёте сквозь однородное магнитное поле, по отношению направления его вектора магнитной индукции В, будет смещаться влево /см. рис. 14б в (1)/.

Предлагаемая выше трактовка по возникновению силы Лоренца во внешней структуре е− −на (е+ −на) при движении сквозь однородное магнитное поле, позволяет в 1− ом приближении ответить на вопрос: "Чем е− −он отличается от е+ −на?"

Ответ:
Их отличие заключается в том, как они ориентируются при движении в пространстве и направленностью процессов, происходящих в экваториальной составляющей их собственного магнитного поля. Выше было показано, что у е− −на и е+ −на, когда они движутся в одном направлении в однородном магнитном поле, направление движения квантов γ + (м) и γ ‾(м) из внешнего магнитного поля по их Э.У.к., с точки зрения стороннего наблюдателя осуществляется в противоположном направлении.

А теперь, после того как дано причинное истолкование механизма возникновения силы Лоренца, можно перейти к рассмотрению функциональных схем движения е− −на и е+ −на в магнитном поле прямолинейного тока. По е− −ну будет разобрана схема распада высокоэнергичного γ −ма кванта в момент его движения через магнитное поле (известный из практики пример подобного распада в камере Вильсона). Позитрон же мы будем задействовать в качестве положительного заряда, каковым пользуются авторы во многих учебниках по физике, ставя во главу объяснения поведения этого заряда только лишь правило левой руки. Постараемся объяснение провести без применения этого правила, используя только лишь те знания, которые были даны выше.

Примечание:

При рассмотрении последующих функциональных схем взаимодействия е− −на и е+ −на с однородным магнитным полем, в основу их движения в этом поле будет взято понятие о вакуумных состояниях полей − состояниях с наименьшей возможной энергией, в которых реальных частиц нет, но есть виртуальные частицы.
Понятие о виртуальных частицах и виртуальных процессах занимает центральное место в современной Квантовой теории поля. По представлениям данной теории "... в пространстве, где нет никаких излучающих электромагнитные волны объектов, тем не менее имеет место электромагнитное поле, которому соответствует нулевая энергия, определяемая формулой Wo = hω/2 (примечание: в данном выражении ? − это циклическая частота, равная числу колебаний в 2π сек.)".
(вместо знака ? воспроизвести символ омега ? в формулах и символ h заменить на h или на ")
Это электромагнитное поле получило название фотонный вакуум, так как ему соответствуют возникающие и исчезающие фотоны с энергией hω/2, которые не распространяются в окружающем пространстве и существуют независимо от того, есть ли в нём какие−либо другие частицы материи. Поэтому их назвали "виртуальными фотонами". Возникновение и исчезновение виртуальных фотонов приводит к выводу, что всё мировое пространство наполнено особой материей, из которой черпаются виртуальные фотоны. (Это выдержка из учебника Ф.А.Королёва "Курс физики". Оптика, атомная и ядерная физика. Учеб. пособие для студентов физ.−мат. фак. пед. Ин−тов. Изд.2 −е, перераб. М., "Просвещение", 1974.).
Реальные частицы рассматриваются как возбуждения соответствующих полей, вызванные взаимодействиями между полями (так, фотоны − возбуждения эл. − магн. поля, электроны и позитроны − возбуждения электронно − позитронного поля и т. д.). В результате взаимодействия электронно − позитронного поля с эл.−магн. полем позитрон и электрон могут перейти в вакуумное состояние (т. е. ненаблюдаемыми, исчезнуть), а их энергия пойдёт на возбуждение электромагнитного поля − рождения фотонов; будет наблюдаться процесс аннигиляции электрон − позитронной пары. Аналогично объясняется и процесс рождения пары (см. "Физика микромира", Маленькая энциклопедия, гл. ред. чл. − корр. АН СССР Д.В.Ширков., изд. "Советская энциклопедия"., М., 1980., стр. 113., "Аннигиляция и рождение пар".).

Необходимость этого примечания обусловлена следующим: предыдущие функциональные схемы взаимодействия электрического поля с зарядами, тоже и магнитного поля, рассматривались с позиции только двух взаимно встречных потоков антиподных квантов электромагнитного поля. То есть е− −он и е+ −он, перемещаясь в этих потоках, постоянно подвергались силовому воздействию со стороны этих потоков. Это воздействие, в зависимости от встречного и попутного потока квантов, соответствующим образом отражалось а пространственной ориентации этих частиц.
В свою очередь, по отношению встречного и попутного потока /γ + (эл); γ ‾ (эл)/, в каждой частице определялось направление обхода квантами γ + (м) и γ ‾(м) их кольцевых Э.У.к. по отношению к стороннему наблюдателю (см. п. 10 − Правило левостороннего буравчика).
При этом хочу обратить внимание Читателя на следующий факт: при движении е− −на в электрическом поле, в потоках квантов γ + (эл) и γ ‾(эл), ориентация его по направлению движения выполнялась потоками этих квантов, причём так, что плоскости с кольцевыми Э.У.к. всегда ориентируются перпендикулярно вектору его скорости Vе− или направлению этих потоков.
Подобная ориентация осуществлялась этими квантами в процессе их взаимодействия с меридиональными Л.П.м. и тем самым достигался разворот е− −на по направлению электрического поля. См. схематичный рис. 1; 17 и 23 в (1).


Вопрос: " А при движении, например, прямолинейного проводника сквозь магнитное поле, в "обязанность" каких квантов или какое поле будет выполнять подобную роль?" См., например, рисунок 18 и 20 в (1).

На этих схемах также не показана меридиональная составляющая магнитного поля электрона (в том числе и у псевдо позитрона на рис 18.).
Или, например, когда тот же электрон движется в пространстве, в отсутствии электрических и магнитных полей. Ведь в соответствии с выводами по ряду ЭМР(1 ÷ ∞), он тоже должен ориентироваться как и при движении в электрическом поле.
Автор считает, что подобную роль должны выполнять потоки виртуальных квантов, которые возникают в пространстве в процессе движения сквозь него любых "элементарных" частиц, в том числе и электронов. В подтверждение, правда косвенно, следует привести опыты Г.Роуланда и А.А.Эйхенвальда в Москве − (см. "Элементарный учебник по физике" под ред. акад. Г.С.Ландсберга", т.2., "Электричество и магнетизм", изд. "Наука", Глав. Ред. физ.−мат. лит., М., 1966 г., стр. 293-294).

Но допустим, что при движении е− −на и т. д. через пространство, виртуальные кванты не взаимодействуют с его Л.П.м., а ориентация осуществляется за счёт квантов γ + (м) и γ ‾(м) внешнего магнитного поля. Тогда, если это поле по отношению электронов будет направлено "сверху − вниз", то при пролёте сквозь него они сориентируются так, что их оси вращения займут вертикальное положение. При этом плоскости с кольцевыми Э.У.к. будут перпендикулярны вектору индукции магнитного поля В. При таком их положении относительно линий индукции поля, они его квантами γ + (м) и γ ‾(м) будут атаковываться по всей длине окружности /см., например, рис. 8 в (1)/.


А с учётом того, что при такой ориентации Э.У.к. относительно линий индукции магнитного поля, эффект позонной экранизации магнитных квантов в системе антиподных Э.У.к. сводится на нет, то Лоренцевы силы возникать в них не будут. В результате при пролёте сквозь внешнее магнитное поле электроны отклоняться от первоначальной траектории не будут. Но практика показывает, что они откланяются. Но чтобы это происходило, необходима их соответствующая ориентация относительно вектора их скорости Vе−. Считаю, что необходимая ориентация достигается за счёт взаимодействия меридиональных Л.П.м. электрона и т.д. с виртуальными квантами из окружающего электрон пространства. Сема подобного взаимодействия подобна схеме рисунка 1 /см. в (1)/.

Только вместо взаимодействия Л.П.м. электрона с γ + (м) и γ ‾(м), происходит процесс взаимодействия с γ + (в) и γ ‾ (в) − пр. Е и П − ия.
В последующем, при анализе функциональных схем всех последующих примеров, мы будем исходить из того, что е− −ны (е+ −ны и т. д. − пр. Е и П −ия!) при движении в окружающем нас пространстве, постоянно взаимодействуют и с попутным, и встречным потоками виртуальных квантов γ + (в) и γ ‾(в).


А теперь, "вооружившись" этим примечанием, приступим к рассмотрению функциональных схем действия внешнего магнитного поля на двигающийся сквозь него электрический заряд. Рассмотренные далее функциональные схемы будут даны только по отношению позитрона. Всё сказанное для позитрона, для электрона буде наоборот.


6.2. Движение положительного заряда (е+ −на) в магнитном поле прямолинейного тока.

Пример 1.
На условном рисунке 77а заряд +q движется вдоль проводника в магнитном поле прямолинейного тока. Справа от этого рисунка даётся условный рисунок по виду А, на котором линии индукции магнитного поля прямолинейного тока и кольцевые Э.У.к. заряда (е+ −на) условно спроектированы на плоскость листа. И те и другие находятся в состоянии суперпозиции. Напомню, что согласно раздела 2 − (см. "Предпосылки антиподно−эквивалентного подхода к электромагнитным явлениям" в данной статье) кольцевые Э.У.к. е+ −на должны располагаться (условно) в плоскости, перпендикулярной направлению вектора скорости е+ −на (е− −на).

В проводнике кванты γ + (эл) "уходят" от стороннего наблюдателя за чертёж, т. е. в том же направлении, что и ток, а γ ‾(эл) в направлении стороннего наблюдателя. Согласно п. 10 (см. п.10 − Правило левостороннего буравчика), γ + (м) по "своим" линиям индукции прямолинейного тока (красные Э.У.к.), по отношению стороннего наблюдателя должны двигаться против часовой стрелки, а γ ‾(м) по "своим" (синие Э.У.к.) − по часовой.






В соответствии с этим Э.У.к. заряда +q (е+ −на) будут "атаковываться" γ + (м) −ми из магнитного поля прямолинейного тока "условно" "снизу" по отношению линии О − О, а γ ‾(м) −ми "сверху".
В свою очередь заряд +q (е+ −он) "удаляется" от стороннего наблюдателя (условно) тоже за чертёж. Для него встречным потоком является поток виртуальных квантов γ ‾(в), а попутным поток квантов γ + (в). Согласно пункта 10 (см. п.10 − Правило левостороннего буравчика) движение первых квантов, а следовательно и γ ‾(м) по "своим" кольцевым Э.У.к. заряда +q (е+ −на), по отношению к стороннему наблюдателю на схеме б, в плоскости листа будет "осуществляться" по часовой стрелке. Вов-вторых, т. е. γ + (в) и, следовательно, γ + (м), тоже по "своим" − против.
С учётом направления движения квантов γ + (м) и γ ‾(м) по Э.У.к. е+ −на, реактивные силы от них будут направлены позонно в сторону проводника. Суммарная же сила Лоренца от этих импульсов, через посредство Э.У.к. будет воздействовать на материальную составляющую заряда +q(е+ −на), находящуюся в его центре (примечание: здесь и далее будем называть её ядром) и он, под её воздействием, при движении вдоль проводника, будет вынужден смещаться влево − в плане рисунка б справа − налево. То есть так, как должно и быть в соответствии с правилом левой руки /см . рис. 9 в (1)/.


Пример 2.
На условной схеме рис. 78а в отличии от схемы рис. 77а, положительный заряд +q (е+ −он) движется (условно) в направлении к стороннему наблюдателю из − за плоскости листа. При этом направление движения заряда и тока по проводнику взаимно противоположны. Так как ток J в данной схеме движется по проводнику в том же направлении, что и на схеме рис.77а, то направление движения квантов γ + (м) и γ ‾(м) по линиям магнитной индукции прямолинейного тока будет тоже.
С точки зрения стороннего наблюдателя γ + (м) по "своим" линиям индукции магнитного поля должны двигаться против часовой стрелки, а γ ‾(м) по "своим", по часовой. Отметим, что направление тока в проводнике на схеме рис. 78а совпадает с направлением движения по нему потока квантов γ + (эл).




В отношении Э.У.к. заряда +q (е+ −на) здесь мы имеем противоположную картину, нежели в схеме рис. 77б. Так как теперь заряд движется (условно) к стороннему наблюдателю из−за плоскости чертежа, то теперь кванты γ + (м) из магнитного поля, после перехода на "свои" Э.У.к. заряда, будут двигаться по ним по часовой стрелке (по отношению стороннего наблюдателя), а кванты γ ‾(м) по "своим" уже против. Отметим также, что первые /γ + (м)/"атакуют" "свои" Э.У.к. условно "снизу" от оси О − О (см. рис. 78б), а вторые /γ ‾(м)/ "свои" Э.У.к. "сверху" − в плане рисунка. Здесь, направление движения квантов γ + (м) и γ ‾(м) мы определяем так же, как и в случае рисунка 77, с помощью виртуальных квантов γ + (в) и γ ‾(в).
Реактивные импульсы или силы Лоренца "заставят" соответствующие участки Э.У.к. "сверху" и "снизу" от оси О − О двигаться в одном направлении − в направлении слева − направо (см. вид А на схеме 78б) в плоскости рисунка. То есть под действием сил Лоренца заряд +q (е+ −он), двигаясь вдоль проводника, всё время будет искривлять свою траекторию в направлении от проводника. То есть всё будет происходить в соответствии с правилом левой руки.

Пример 3.
В отличие от рисунков 77а и 78а, где заряд +q (е+ −он) перемещался вдоль проводника, в схеме рис. 79а заряд условно приближается к проводнику.



Для выявления направления действия Лоренцевых сил на Э.У.к. заряда, обратимся к рисунку 79б, на котором кольцевые Э.У.к. позитрона условно изображены в плоскости листа, а магнитное поле прямолинейного тока по отношению заряда направлено сверху − вниз.
Двигаясь в направлении к проводнику, кольцевые Э.У.к. позитрона пересекают линии индукции магнитного поля прямолинейного тока и кванты этого поля совершают переход с линий индукции прямолинейного тока на Э.Ук. е+ −на.
Так как позитрон удаляется от стороннего наблюдателя, то встречным для него потоком будет являться поток виртуальных квантов γ ‾(в), а попутным γ + (в). В соответствии с пунктом 10 (см. п.10 − Правило левостороннего буравчика) и принципом Единства и Подобия, кванты γ ‾(в), "двигаясь" в направлении стороннего наблюдателя, должны с его точки зрения обходить "свои" кольцевые Э.У.к (е+ −на) по часовой стрелке, а кванты γ + (в), так как они движутся от стороннего наблюдателя, "свои" Э.У.к. против часовой. Соответственно, и по направлениям в Э.У.к будут перемещаться кванты γ + (м) и γ ‾(м).

К этому следует добавить, что кванты γ ‾(м) магнитного поля (условно) "атакуют" "свои" Э.У.к. е+ −на (условно) сверху от осевой О − О, а γ + (м) снизу. Реактивные усилия от квантов обоих видов, вынудят и "верхние", и "нижние" участки Э.У.к., с момента движения позитрона в магнитном поле прямолинейного тока, постоянно смещаться в направлении справа − налево в плане рисунка б. А в плане рисунка а, е+ −он (заряд) под действием сил Лоренца будет вынужден, пока он движется в направлении к проводнику, одновременно совершать перемещение и вдоль проводника. На схеме рисунка 79а (условно) "вниз".
Проведённый выше анализ схемы рисунка 79 был выполнен без применения правила левой руки, но результат, как и в случаях с рисунками 77 и 78, не находится в противоречии с этим искусственным правилом.

Пример 4.
Схема опыта − см. рис. 80, характерна тем, что кольцевые Э.У.к. заряда +q (е+ −на) не пересекают линии индуктивности магнитного поля. При таком движении, как показывает практика, кванты γ + (м) и γ ‾(м) магнитного поля прямолинейного тока не взаимодействуют с Э.У.к. заряда, а при отсутствии соответствующих реактивных импульсов, заряд остаётся как бы в покое.



В то же время эта функциональная схема сродни схеме рис. 8 /см. в (1)/, когда кольцевые Э.У.к. заряда (е+ −на), по всей длине окружности "атакуются" квантами γ + (м) и γ ‾ (м) из магнитного поля прямолинейного тока. А так как движение этих квантов по "своим" Э.У.к. заряда осуществляется взаимно противоположно, то суммарные реактивные силы от импульсов взаимно компенсируются и как следствие, сила Лоренца равна нулю. При этом следует отметить, что хотя суммарная сила Лоренца и равна нулю, но по отдельности каждая кольцевая, антиподная система кольцевых, экваториальных Э.У.к. заряда (е+ −на) находится под постоянным реактивным воздействием "своих" квантов.

Пример 5.
В разных учебниках по физике приводится фотография или схематичный рисунок разлёта в разные стороны е− −на и е+ −на после распада высокоэнергичного γ −ма кванта в пузырьковой камере Вильсона, помещённой в сильное однородное магнитное поле /см. рис. 15 и 16 в (1)/. При этом направление отклонения частиц от первоначальной траектории мотивируется наличием у них электрического заряда.


Выше, при анализе функциональной схемы движения е− −на (е+ −на) в электрическом поле /см. рисунок 21 и 22 в (1) и пояснения к ним/, было показано, что понятие электрический заряд является искусственной характеристикой, позволяющей отличать подобные частицы одну от другой. Покажем, что и в случае с е− −ом и е+ −ом, их разлёт в камере Вильсона обусловлен не наличием у них искусственно приписываемой им характеристики, а обусловлен соответствующими процессами, происходящими в их внешней структуре под действием магнитного поля. Для этого обратимся к рисунку 15 /в (1)/.

На рисунке 15 /в (1)/, схематично показано, что вектор магнитной индукции отклоняющего поля В перпендикулярен плоскости чертежа (листа) и направлен за чертёж, в сторону от стороннего наблюдателя. Согласно правила левой руки, е− −он отклоняется вправо, а е+ −он влево в плане рисунка. С целью наглядности видоизменим схему этого рисунка и расположим его так, чтобы сторонний наблюдатель, в проекции на плоскость листа видел кольцевые Э.У.к. обеих частиц. Это позволяет наглядно видеть направление действия лоренцевых сил в системе Э.У.к. обеих частиц /см. рис. 16 в (1)/.

Хотя е− −он и е+ −он "удаляются" от стороннего наблюдателя в одном направлении, но встречные и попутные потоки для них будут разные. Для е− −на встречным должен быть виртуальный поток γ + (в), а попутным поток γ ‾(в). Для е+ −на встречным будет виртуальный поток γ ‾(в), а попутным γ + (в). Кванты этих потоков, после того как пройдут сквозь них и окажутся на их Э.У.к., будут передвигаться по ним в определённом направлении − (примечание: проход Фликкер выброса сквозь электрон и позитрон будет рассмотрен в структурно−функциональном анализе ряда ЭМР(1 ÷ ∞) в отдельной статье).

В е− −не, по отношению стороннего наблюдателя, кванты γ ‾(в) по "своим" Э.У.к. будут двигаться против часовой стрелки, а кванты γ + (в) по "своим" по часовой. В позитроне же γ + (в) против часовой, а γ ‾(в) соответственно по. По этим направлениям будут двигаться и кванты γ + (м) и γ ‾(м), которые из магнитного поля, имеющего направление "сверху" − "вниз", перейдут на Э.У.к. обеих частиц.
Кванты γ ‾(м) магнитного поля "атакуют" "свои" кольцевые Э.У.к. обеих частиц (условно) "сверху" и на участках этих (сверху от оси О − О, см. рис. 16 в (1)) колец будут двигаться навстречу друг другу. Соответственно реактивные импульсы от них будут действовать на эти участки в обратном направлении. То есть силы Лоренца эти участки частиц будут отодвигать друг от друга. То же самое будет и с нижними участками, которые находятся под воздействием квантов γ + (м) внешнего магнитного поля. Под воздействием соответствующих реактивных импульсов они так же, как и верхние будут отодвигаться друг от друга.
Усилия от Лоренцевых сил, через посредство кольцевых Э.У.к постоянно будут воздействовать на ядра частиц и последние, пока они пролетают сквозь магнитное поле, будут всё дальше и дальше отходить друг от друга. Траектория их движения после распада высокоэнергичного γ −ма кванта будет определяться двумя факторами: направлением их движения и направлением действия Лоренцевых сил. Так как оба эти направления взаимно перпендикулярны, то результатирующие траектории движения обеих частиц будут кривые, концы которых удаляются друг от друга по мере движения частиц сквозь магнитное поле.
Представляется, что подобная трактовка причины отклонения обеих частиц в магнитном поле, со стороны Читателя не вызовет особых возражений, ибо она находится в полном согласии с правилом левой руки.

Функциональная схема разлёта е− −на и е+ −на в реакции распада высокоэнергичного γ −ма кванта примечательна и в другом отношении. В определённой степени она подобна схеме отталкивания проводников, по которым течёт электрический ток в разных направлениях /см. рис. 11 и 12 в (1)/. Отталкивание двух проводников в этой схеме происходит за счёт перехода квантов γ + (м) и γ ‾(м) с линий индукции магнитного поля одного проводника, на линии магнитной индукции другого. При этом системы кольцевых Э.У.к. обоих проводников или же электронов проводимости, находятся в состоянии суперпозиции, т. е. имеет место взаимного проникновения магнитных полей в пространство друг друга.
Схожий процесс имеет место и в случае разлёта е− −на и е+ −на в реакции распада высокоэнергичного γ −ма кванта, особенно на начальной стадии их отхода друг от друга. В этот момент их ядра максимально сближены и, следовательно, степень суперпозиции их кольцевых Э.У.к. максимальна. Здесь так же, как и в случае с проводниками, следует учитывать фактор плотности кольцевых Э.У.к. обеих частиц , определяющий густоту расположения Э.У.к. в радиальном от частиц направлении. Так, в случае с проводниками, линии индукции их магнитных полей вблизи от них, располагаются гуще, нежели вдали от них. Тоже самое должно быть и в случае с Э.У.к. у е− −на и е+ −на − пр. Е и П −ия! Учёт этого обстоятельства, существенным образом скажется на количестве квантов, участвующих в обменном процессе между системами кольцевыми Э.У.к. обеих частиц.
В самом начале распада, когда электрон и позитрон максимально сближены, количество квантов, участвующих в обменном процессе будет максимально. Следовательно, и максимальны будут силы, направленные на их разлёт в противоположные стороны. При этом следует исходить из того, что отталкивание е− −на от е+ −на и наоборот, согласно функциональной схемы /см. условный рис. 16 в (1)/ происходит на фоне двух силовых факторов, действующих между частицами.
Один фактор − это Лоренцевы силы, возникающие в системе кольцевых Э.У.к. каждой частицы от "перехода" квантов γ +(м) и γ ‾(м) из внешнего магнитного поля на их Э.У.к. Другой − обусловлен возникновением обменных сил в системе кольцевых Э.У.к. обеих частиц от перехода" квантов γ + (м) и γ ‾(м) с кольцевых Э.У. электрона на подобные позитрона и наоборот. Наличие этих двух силовых факторов и обусловливает разлёт электрона и позитрона (образно) с "удвоенной" силой.
В последующем, по мере отхода электрона от позитрона, силовой фактор, обусловленный "переходом" виртуальных квантов из системы кольцевых Э.У.к. е− −на в систему кольцевых Э.У.к. е+ −на и наоборот, убывает в виду того, что густота кольцевых Э.У.к. частиц вдали от их ядер меньше, нежели вблизи от них, а также из−за того, что плоскости кольцевых Э.У.к., по мере разлёта частиц, всё больше и больше располагаются под углом друг к другу.
На определенном расстоянии между удаляющимися частицами, суперпозиция кольцевых Э.У.к. электрона и позитрона прекратится вовсе. С этого момента, каждая из частиц и электрон, и позитрон будут находиться под действием только Лоренцевых сил со стороны внешнего магнитного поля.

На начальном этапе разлёта е− −на и е+ −на, после распада высокоэнергичного γ −ма кванта во внешнем магнитном поле, кроме вышеназванных двух реактивных, силовых факторов, можно "усмотреть" и третий, который наряду с первыми двумя действует по мере их отхода друг от друга. Этот третий обусловлен наличием у е− −на и е+ −на собственных электрических полей в виде Л.П.эл. (примечание: на рис. 16 в (1) они отсутствуют), которые подобно кольцевым Э.У.к., на начальной стадии их разлёта, находятся в суперпозиции /см. условный рис. 12а и б в(1)/.
Между ними, так же как и между кольцевыми Э.У.к., происходит обмен виртуальными квантами γ + (эл) и γ ‾(эл). Но направленность реактивных процессов в системе Л.П.эл., в отличии от системы кольцевых Э.У.к., совсем противоположная. Если в системе кольцевых Э.У.к действие реактивных импульсов направлено на отталкивание обеих частиц друг от друга, то действие реактивных импульсов в системе Л.П.эл. имеет обратную направленность − на их притяжение .

Вышеприведённая схема разлёта е− −на и е+ −на была проанализирована с позиции внешней структуры обеих частиц. При этом основными "представителями" их внешней структуры выступали экваториальные Э.У.к., а также электрические Л.П.эл. их собственных электрических полей. На фоне этих составляющих остались без внимания меридиональные Л.П.м., т. е. одна из составляющих магнитного поля е− −на и е+ −на. По идее, подобно Э.У.к. и Л.П.эл., и меридиональные Л.П.м. должны подвергаться воздействию со стороны магнитного поля.
В то же время, из практики мы знаем, что при возникновении отклоняющей заряды силы Лоренца, других побочных, силовых факторов не наблюдается.
Если в этом деле исходить из схемы рисунка 1 в (1), то летящие сквозь магнитное поле е− −он или е+ −он, под воздействием его потоков квантов γ + (м) и γ ‾(м) на меридиональные Л.П.м., должны по мере прохождения зоны магнитного поля разворачиваться так, чтобы их ось вращения стала параллельна линиям индукции магнитного поля, т. е. по направлению совпала бы с направлением потоков γ + (м) и γ ‾(м) этого внешнего поля. При этом плоскости кольцевых Э.У.к. заняли бы положение, параллельное вектору их скорости и тем самым было бы нарушено требование перпендикулярности направлению движения частиц в пространстве.
На самом деле этого не происходит. Но чем это обусловлено, ответить пока трудно. Не исключено, что силовой фактор со стороны виртуальных потоков по направлению движения обеих частиц, "удерживающий" их в надлежащей ориентации, намного превосходит силовой фактор со стороны внешнего магнитного поля. Но это, пока что предположение и ответа по данному вопросу у автора нет.

Информация к размышлению.

Из практики по распаду высокоэнергичного γ −ма кванта во внешнем магнитном поле, в камере Вильсона, достоверно следует, что е− −он и е+ −он от точки распада удаляются в противоположные стороны. Это в основном происходит под действием реактивных импульсов, получаемых системой кольцевых Э.У.к. от квантов γ + (м) и γ ‾(м) из внешнего магнитного поля после того, как они окажутся на "своих" Э.У.к. в частицах. К этому времени кольцевые Э.У.к. должны соответствующим образом сориентироваться по отношению встречных (попутных) потоков виртуальных квантов или фотонов. Как это происходит, мы выше разобрали на примере движения е− −на и е+ −на во внешнем электрическом поле. Но подобный разбор предопределял их движение в среде двух взаимно встречных потоков, которые по отношению друг другу были антиподами. То есть, с одного направления двигался только поток квантов, например, γ ‾(эл), а встречным ему был поток квантов γ + (эл). Эта схема без особых трудностей позволяла причинно объяснить поведение этих частиц как в электрическом, так и в магнитном поле.

Но тут правомерен следующий вопрос: "А как обстоит дело с ориентацией е− −на и е+ −на при их перемещении в пространстве, например, в вакууме? Ведь в вакууме они будут подвергаться совместному действию потоков квантов γ + (в) и γ ‾(в) как со стороны встречного, так и со стороны попутного направлений. При этом, исходя из изотропности окружающего пространства их плотность должна быть одинакова во всех направлениях телесного угла 4π.
Если в этом вопросе исходить из изотропности окружающего пространства и схемы переориентации е− −на и е+ −на по направлению движения, то вынуждены будем признать, что подобная их переориентация в вакууме под воздействием потоков виртуальных квантов γ + (в) и γ ‾(в), движущихся в одном направлении, в принципе невозможна. Ведь в этом случае, из рассмотрения следует исключить эффект позонной экранизации квантов (фотонов) во внешней структуре е− −на и е+ −на.
То есть мы оказываемся перед парадоксом: с одной стороны, предложенная функциональная схема поворота е − −на и е+ −на не позволяет причинно объяснить их поворот в вакууме, а с другой − их переориентация происходит и свидетельством тому является их разлёт после реакции распада высокоэнергичного γ −ма кванта в камере Вильсона.
Пока не представляется возможным преодолеть данный парадокс и поэтому, несмотря на его наличие, мы будем исходить из объективного факта, что при движении в пространстве система кольцевых Э.У.к. данных и т.д. частиц (пр. Е и П −ия!), всегда ориентируется перпендикулярно к направлению их движения или вектору их скорости. При этом встречным потоком для е− −на будет поток квантов γ + (в), а для е+ −на − поток квантов γ ‾(в) − (примечание: о наличии в пространстве самостоятельных потоков вертуальных квантов γ + (в) и γ ‾(в) можно говорить лишь с определённой степенью условности, ибо как таковых в окружающем нас пространстве нет. Тогда почему автор все время апеллирует этими потоками при анализе схем электромагнитного характера?

Ответ: То что таковые виртуальные кванты в пространстве есть, автор руководствуется положениями Квантовой теории поля. Но т. к. элементарные частицы перемещаются в пространстве, то подобное движение приводит к тому, что по отношению их возникают псевдо потоки виртуальных квантов, которые, будучи захвачены Л.П.эл. и Л.П.м. частицами, одновременно и ориентируют их в пространстве, и участвуют в создании вокруг них Э.У.к., т. е. экваториальной составляющей их магнитного поля.
_________________________

7. Электромагнитная индукция.

Из практики известно, что в проводящем контуре, находящемся в переменном магнитном поле, возникает индуцированное электрическое поле, характеристикой которого является электродвижущая сила индукции. В замкнутом контуре возникает электрический ток, называемый индукционным током, а всё явление называется электромагнитной индукцией. Это явление было обнаружено Фарадеем опытным путём.
Серией опытов Фарадей показал, что в замкнутых проводящих контурах, находящихся в переменном магнитном поле, возникает электрический индукционный ток независимо от того, как достигается изменение во времени магнитного потока сквозь площадь поверхности, ограниченной контуром. Магнитный поток, пронизывающий площадь поверхности контура, может изменяться с течением времени благодаря деформации или перемещению контура во внешнем магнитном поле, а также потому, что индукция магнитного поля может быть переменной.
Электромагнитная индукция характеризуется электродвижущей силой (Э.Д.С.) электромагнитной индукции. Термин "электродвижущая сила" обозначает ту причину, которая разделяет заряды и тем самым создаёт электрическое поле, которое, собственно говоря, и движет заряды.


ЭДС считается положительной, если магнитный момент Рм соответствующего ей индукционного тока є(ι) в контуре образует острый угол с линиями магнитной индукции того поля, которое наводит этот ток. В противном случае ЭДС считается отрицательной, когда этот угол > 90° (см. рис. 83а и б).

ЭДС электромагнитной индукции численно равна и противоположна по знаку скорости изменения магнитного потока сквозь площадь поверхности, ограниченной этим контуром:

Е(ин) = − ΔФ/Δ t
Знак минус в законе ЭДС индукции выражает правило Ленца: индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Эти краткие сведения об электромагнитной индукции, в основном взяты автором из "Справочного Руководства по Физике" авт. Б.М.Яворский, Ю.А.Селезнёв, изд. "Наука", Главная Редакция физико-математической литературы., М., 1979. Подобно этому руководству, также и в других учебниках, более углублённая трактовка этого явления не даётся, а в дополнение к этим, общеизвестным сведениям, даются примеры, в которых суть происходящих событий трактуются с позиции силы Лоренца и правила правой руки.
По этому правилу определяется направление напряженности стороннего электрического поля электромагнитной индукции в прямолинейном проводнике, движущимся в магнитном поле: если ладонь правой руки расположить так, чтобы вектор магнитной индукции В входил в ладонь, а отставленный на 90° большой палец совпадал с направлением перпендикулярной к проводнику составляющей его скорости, то вытянутые четыре пальца укажут направление напряжённости стороннего электрического поля электромагнитной индукции, возникающего в проводнике − см. рисунок 84.





Напомню, что за направление электрического поля в проводнике принято то направление, в котором движутся положительные заряды.

7.1. Э.Д.С. индукции в движущихся проводниках.

А теперь попробуем на электромагнитную индукцию взглянуть без правила правой руки, а с позиции тех сведений, которые даны выше при анализе движения положительного заряда (е+ −на) в магнитном поле прямолинейного тока. С этой целью рассмотрим движение отрезка прямолинейного проводника в стационарном однородном магнитном поле, но для начала воспользуемся теми сведениями, которые приводятся в "Справочном Руководстве по Физике" авт. Б.М.Яворский, Ю.А.Селезнёв , изд. "Наука", Гл. ред. физ. − мат. лит., М., 1979, (см. в справочнике стр. 236 − 237).

"... При движении проводника в магнитном поле на его положительные и отрицательные заряды действует сила Лоренца. Под действием силы Лоренца в проводнике происходит разделение зарядов: положительные и отрицательные заряды накапливаются на противоположных концах проводника. Эти заряды создают внутри отрезка проводника кулоновское поле. Перемещение зарядов под действием силы Лоренца будет происходить до тех пор, пока сила, действующая на заряд в кулоновском поле, не уравновесит силу Лоренца.
ЭДС индукции в отрезке проводника является работой по перемещению единичного положительного заряда вдоль проводника.
Действие лоренцевых сил на заряды проводника аналогично действию некоторого электрического поля, направленного противоположно кулоновскому полю. Это поле создаётся не кулоновскими силами, а силами магнитного происхождения − силами Лоренца. Поэтому электрическое поле, характеристикой которого является ЭДС индукции, является сторонним электрическим полем."

Попробуем теперь к этим сведениям подойти с позиции того же е− −на (е+ −на), имеющего внутреннюю и внешнюю структуры /см. рис. 27.1; 27.2; 27.3 и 27.4 в (1)/ и движущимся в стационарном однородном магнитном поле. На некоторое время "забудем" о существовании правила правой руки.
Рассмотрим движение прямолинейного проводника в этом магнитном поле. В качестве проводника используем его условную модель, в которой наряду с подвижными е− −ми имеются и подвижные псевдо е+ −ны /см. рис. 18 в (1)/. Такая абстрактная модель проводника позволит нам, с позиции принципа Единства и Подобия рассмотреть поведение положительных и отрицательных в нём зарядов, не взаимодействующих между собой. Подобная абстрактная схема идентична поведению подвижных электронов и положительных ионов при прохождении электрического тока через проводники 2 (второго) рода, т. е. через электролиты. Но сами по себе обе схемы принципиально отличаются друг от друга тем, что в абстрактной (условной) схеме электроны и псевдо позитроны приводятся в движение Лоренцевыми силами, а в ей подобной − силами, действующими со стороны вешнего электрического поля, прикладываемого к проводникам 2 −го рода. Это различие сказывается и на пространственной ориентации зарядов во время их движения по проводнику.

Выше, при анализе движения положительного заряда (е+ −на) в магнитном поле, автор руководствовался положением Квантовой теории поля, согласно которого в окружающем нас пространстве наличествуют виртуальные кванты. Но к вопросу о таких квантах, подходит с антиподных позиций. Подобно е− −ну и е+ −ну, протону и антипротону, кваркам и антикваркам и т. д., в Природе наличествуют и антиподные фотоны γ + и γ ‾ или кванты электромагнитного поля (пр. Е и П −ия!).
Учёт этого обстоятельства, позволяет в 1 −ом приближении, причинно объяснять различные явления по электромагнетизму. Подобной точки зрения будем придерживаться и в дальнейшем при анализе электромагнитной индукции. Подойдем к объяснению этого явления с причинных позиций, но для начала, с антиподных позиций, дадим объяснение опытов Роуланда и А.А.Эйхенвальда в Москве (см. "Элементарный учебник по физике" под ред. акад. Г.С.Ландсберга, т.2., "Электричество и магнетизм", изд. "Наука", Глав. Ред. физ.-мат. лит., М., 1966 г., стр. 293 − 294).

Суть этих опытов в следующем:
"... по круговому проволочному витку протекает ток. При этом, как мы знаем, возникает магнитное поле, которое можно обнаружить по отклонению магнитной стрелки, подвешенной на нити вблизи витка. Схематично опыт изображён на рис. 85. На рис. 85а виток показан в плоскости чертежа, а магнитная стрелка − перпендикулярно к этой плоскости. На 85б тот же виток изображён перпендикулярно к плоскости чертежа, а стрелка лежит в этой плоскости. На рис. 85в, пунктиром показан путь положительно заряженного тела, движущегося по окружности. Отклонение магнитной стрелки, вызванное этим движением, такое же, как при протекании тока по витку проволоки (рис. 85г).


Эти опыты доказывают, что движущееся заряженное тело создаёт вокруг себя магнитное поле совершенно такое же, как обычный электрический ток. Они подтверждают, таким образом, предположение, что наблюдаемое нами магнитное поле есть результат наложения магнитных полей, создаваемых отдельно движущимися заряженными частицами − электронами или ионами (примечание: данный текстовой материал и схема рисунков 85 взяты автором из "Элементарного учебника по физике" под ред. акад. Г.С.Ландсберга , т. 2, М., 1966 г., стр. 293 − 294)".

А теперь внесём соответствующие уточнения по данным опытам. Для этого Читателю следует обратиться к статье (1), где приводится схема опыта Г.Х. Эрстеда от 1820г./см. в (1) рис.5/. Эта схема с причинных позиций "объясняет" причину поворота магнитных стрелок в магнитном поле прямолинейного тока. Они разворачиваются под действием квантов этого поля, действующих в двух, взаимно противоположных направлениях на Л.П.м. магнитного поля магнитных стрелок.




Кванты внешнего магнитного поля, перемещающиеся по кольцевым линиям индукции вокруг прямолинейного проводника, не могут свободно проникать в пространство магнитного поля магнитной стрелки. Они вынуждены это пространство "обходить" стороной. В окружающей нас действительности показателен пример с магнитным полем Земли. Потоки соответствующих частиц , которые движутся от Солнца к Земле, не просто захватываются магнитным полем Земли. Они захватываются меридиональными линиями её магнитного поля и затем движутся вдоль них к магнитным полюсам нашей планеты. Способность силовых линий магнитного поля планеты переориентировать движение частиц в пространстве при подлёте к Земле, является защитной мерой от их губительного действия на всё живое на поверхности Земли.
Рассматривая магнитное поле Земли и магнитной стрелки с позиции принципа Единства и Подобия, мы должны сказать, что у Земли обходными путями для частиц являются магнитные силовые линии её магнитного поля, а у магнитной стрелки, её меридиональные линии магнитной индукции Л.П.м.
В процессе "перехода" квантов γ + (м) и γ ‾(м) с линий индукции магнитного поля прямолинейного тока, на меридиональные Л.П.м. магнитной стрелки, последние от этих квантов получают реактивные импульсы. С учётом эффекта позонной экранизации, который имеет место по отношению этих квантов в системе меридиональных Л.П.м. магнитной стрелки, и возникает момент, который разворачивает её так, что она, если смотреть на стрелку сверху, становится в положение перпендикулярное проводнику.
Подобный ход событий происходит и в опыте с проволочным витком. Ведь круглый проводник всегда можно сделать из прямолинейного и рассматривать взаимодействие его магнитного поля с магнитной стрелкой с тех же позиций, что и в случае прямолинейного тока − пр. Е и П −ия.

Отличительной особенностью схемы рис. 85а, по отношению к схеме рис. 85в, является то, что по круглому проволочному витку пропускается ток. Но ток по витку "пойдёт" только тогда, когда к нему будет приложено внешнее, стороннее электрическое поле. Кванты γ + (эл) и γ ‾(эл) этого поля, двигаясь вдоль проводника со световой скоростью, взаимодействуют с электронами проводимости и, с одной стороны, производят их переориентацию так, что их оси вращения ориентируются по направлению потоков γ + (эл.) и γ ‾(эл.) в кольцевом проводнике, взаимодействуя с меридиональными Л.П.м. их магнитного поля /см. рис. 1 в (1)/, а с другой, через посредство электрических Л.П.эл. их собственного электрического поля, "заставляют" электроны перемещаться вдоль проводника /см. рис. 21 в (1)/.

Но на этом взаимодействие квантов γ + (эл) и γ ‾(эл) из внешнего электрического поля в проводнике с е− −ми проводимости не заканчивается. Если потоки этих квантов (условно) "осуществляют" переориентацию электронов и их продвижение вдоль проводника, то в "обязанность" самих е− −ов входит переориентация направления движения этих квантов. С движения вдоль проводника они переводят их на движение по своим экваториальным Э.У.к. Для этого кванты γ + (эл) и γ ‾(эл) должны пройти сквозь е− −ны проводимости по их внутренним проходам.
Сначала войти в их осевой диаметральный О.Т., который совпадает с осью вращения е− −на /см. условные рис. 27.1; 27.2 и 27.3 в (1)/, а пройдя его и его фокусы, попасть в его керн. В нём они должны развернуться примерно под углом 90° и из него уйти в экваториальные О.Т. По выходе из них кванты (фотоны) должны достичь кольцевые Э.У.к. е− −ов и совершить переход (перескакивание) на них, перейдя при этом в разряд квантов γ + (м) и γ ‾(м) − (примечание: о таком переходе и об О.Т. − нулевом туннеле, речь будет идти в отдельной статье, в которой будет дан структурно−функциональный анализ рядов ЭМРN и ЭМР(− ∞ ÷ ∞)).

Не исключено, что подобный переход тоже сопровождается передачей Э.У.к. соответствующих реактивных импульсов. Но учитывая, что движение перешедших квантов из проводника в экваториальную составляющую магнитного поля е− −ов проводимости осуществляется по этим Э.У.к. во взаимно противоположных направлениях, то суммарные реактивные импульсы в обеих системах антиподных Э.У.к. электронов, будут взаимно компенсировать друг друга и внешне, никакого побочного эффекта сторонним наблюдателем отмечено не будет.
В последующем, движущиеся по Э.У.к. кванты γ + (м) и γ ‾ (м), которые уже являются представителями магнитного поля прямолинейного (о тока, после определённого (?...) Времени пребывания на этих Э.У.к., должны покинуть их и "уйти" в экваториальные О.Т. е− −ов проводимости; затем в их керн и далее перейти в их осевой диаметральный О.Т. и т. д., т. е. (образно) − уйти в проводник.

Вышесказанное по схеме рисунков 85а и б в отношении проволочного витка, можно с точки зрения пр. Е и П −я отнести и к схеме движения положительного заряда по круговой орбите. Но тут правомерен вопрос: "Если наличие квантов γ + (эл) и γ ‾(эл) в проволочном витке обусловливается действием на проводник стороннего электрического поля, то откуда берутся эти же кванты в случае заряженного тела (рис. 85в и г). Ведь с точки зрения пр. Е и П −ия, одинаковость конечного результата − возникновение в окружающем пространстве магнитного поля, есть следствие взаимодействия соответствующих квантов с электронами и положительными ионами.
И вот тут, как бы мы не гадали, но придётся объективно признать, что в случае положительно заряженного тела, двигающегося по круговой орбите, оно (образно) "черпает" кванты γ + (эл) и γ ‾(эл) из окружающего пространства. Следовательно, мы должны признать, что в окружающем нас пространстве, причём из − в + " ∞ " −ть, постоянно присутствуют соответствующие кванты и таковыми, с учётом Квантовой теории поля, являются виртуальные кванты или фотоны. Но не просто кванты одного вида, а кванты γ + (в), γ ‾(в) и γ ° (в).
А так как в качестве положительного заряда выступают положительно заряженные ионы,то из этого следует, что эти ионы смогут переориентировать кванты γ + (в) и γ ‾ (в) из окружающего пространства на свои экваториальные Э.У.к. только в том случае, если эти кванты войдут в непосредственный контакт с ними. Но так как ионы находятся в массиве материального тела, то непосредственный контакт будет, если виртуальные кванты γ + (в) и γ ‾(в) будут свободно проникат (каналировать) в заряженное тело или тот же проводник, и проходя его насквозь, не встречать на своём пути сопротивления.

А теперь, попробуем вышесказанное применить в анализе тех функциональных схем по электромагнитной индукции, в которых её возникновение можно истолковать с помощью Лоренцевых сил, т. е. в движущихся проводниках (примечание: для наглядного истолкования э.д.с. индукции нельзя пользоваться силами Лоренца в тех случаях, когда индукция обусловлена изменением напряжённости поля в неподвижных проводниках − см. "Элементарный учебник физике" под ред. акад. Г.С.Ландсберга, т.2, М.,1966 г., ј143, стр. 337 − 338).
Проводя его, мы должны осознавать, что итоговый результат подобного анализа должен строго соответствовать тем правилам, которые применяются на практике в отношении индукционного тока. Рассмотрению подлежат несколько функциональных схем и первой в этом списке будет схема движения прямолинейного проводника в стационарном однородном магнитном поле.
Рассмотрим упрощённый вариант подобного движения, когда проводник движется перпендикулярно силовым линиям магнитного поля и вектор его скорости V перпендикулярен В /см. рис. 10 в (1)/. Напомню, что в качестве проводника при анализе будет использован его условный аналог /см. рис . 18 в (1)/, в котором наряду с подвижными электронами присутствуют и подвижные псевдо позитроны " е+ ". Последние используются как аналог подвижных положительных зарядов и при движении вдоль проводника не взаимодействуют с подвижными электронами.
При таком движении, проводник квантами γ + (м) и γ ‾(м) из внешнего магнитного поля, имеющего направление сверху вниз, "атакуется" (условно) "сверху" и "снизу". "Сверху" γ ‾(м) квантами, а "снизу" − γ + (м) квантами. Одновременно проводник подвергается каналированию виртуальными квантами γ + (в) и γ ‾(в) из окружающего его пространства, совпадающих по направлению с направлением его движения. При этом встречным, виртуальным потоком для подвижных е− −ов в проводнике будет поток виртуальных квантов γ + (в), а попутным, соответственно поток квантов γ ‾(в). Для псевдо позитронов, встречным будет поток виртуальных квантов γ ‾(в), а попутным, поток квантов γ + (в).

Так как эти кванты на подвижные в проводнике е− −ны и псевдо е+ −ны "должны оказывать" такое же действие, как и кванты из внешнего электрического поля, прикладываемого к проводнику, то в целях отличия электрических квантов от виртуальных, мы поступим так же, как это делали до сих пор. Электрическими, т. е. в проводнике, будут кванты γ + (эл) и γ ‾(эл). Виртуальными будут кванты γ + (в) и γ ‾(в). Одновременно с этим, в целях отличия электрических квантов от магнитных, последние, как и прежде, будем обозначать в виде γ + (м) и γ ‾(м). Это те кванты, которые движутся по силовым линиям индукции внешнего магнитного поля или по кольцевым Э.У.к. е− −ов и псевдо "е+ −ов", а также по меридиональным линиям Л.П.м., меридиональной составляющей их магнитного поля.
В принципе, ни какого различия между электрическими и магнитными квантами нет (?...). Это сделано только с одной целью − акцентировать внимание Читателя на тот путь, по которому или вдоль которого кванты перемещаются в пространстве. Электрические − вдоль линий напряжённости соответствующих электрических полей, а магнитные − вдоль линий индукции, тоже соответствующих магнитных полей. При этом следует иметь в виду: в процессе перехода квантов из одного вида поля, в поле другого вида, у них должен меняться и путевой индекс.

Итак, когда условный проводник /см. рис. 18 в (1)/ движется перпендикулярно силовым линиям внешнего магнитного поля, то как было сказано выше, он одновременно "атакуется" двумя взаимно перпендикулярными потоками квантов. При этом кванты γ + (м) и γ ‾(м) внешнего магнитного поля "атакуют" проводник и "сверху", и "снизу". Направление их "атаки" совпадает с направлением вектора магнитной индукции В внешнего магнитного поля, сквозь который движется проводник.



В отличии от этого потока квантов, потоки виртуальных квантов γ + (в) и γ ‾(в), по направлению совпадают с направлением вектора скорости V проводника или наличествующих в нём е− −ов и псевдо "е+ −ов" проводимости. Один из этих потоков является встречным, а другой попутным. Но следует заметить, что е− −ны и псевдо "е+ −ны" "подвергаются действию" качественно разных встречных и попутных потоков квантов.
Повторю: для е− −на встречным является поток γ + (в), а попутным, соответственно, γ ‾(в). Для псевдо "е+ −на" встречным является поток квантов γ ‾ (в), а попутным поток γ + (в). Эти потоки насквозь каналируют проводник и вступают в нём во взаимодействие с е− −ми и псевдо "е+ −ми". Их основная задача состоит в переориентации последних, а также заставить их принудительно двигаться в направлении, совпадающим с их направлением в пространстве.

Пространственная переориентация подвижных е− −ов и псевдо "е+ −ов" внутри проводника приведёт к тому, что их экваториальные (условные) плоскости с кольцевыми Э.У.к. займут положение, перпендикулярное направлению потоков квантов γ + (в) и γ ‾(в). Из этого следует, что плоскости кольцевых Э.У.к. е− −ов и псевдо е+ −ов расположатся вдоль проводника, перпендикулярно вектору его скорости, и в таком положении Э.У.к. будут двигаться сквозь внешнее магнитное поле вместе с проводником.
А так как Э.У.к. являются конструктивной основой одной из составляющих магнитного поля вокруг проводника, то их расположение вдоль проводника приведёт к образованию экваториальной составляющей магнитного поля необычной формы. Все Э.У.к расположатся в сравнительно тонком слое с двух сторон от проводника и направление этого слоя будет совпадать направлением вектора индукции внешнего магнитного поля; ведь по условию проводник движется перпендикулярно линиям индукции внешнего магнитного поля. Толщина этого слоя в пределе будет равна диаметру проводника. При этом всегда следует иметь в виду, что кроме экваториальной составляющей магнитного поля электронов (и псевдо позитронов), у них также наличествует и меридиональная составляющая их магнитного поля, которая на схемах в ряде случаев отсутствует /см. например, рис. 18 и 20 в (1)/, а также и Л.П.эл., т. е. силовые линии их собственного электрического поля. Ведь пространственная ориентация электронов и псевдо позитронов относительно потоков виртуальных квантов е− это прерогатива меридиональных составляющих их магнитного поля.
Движение проводника связано с пересечением линий индукции внешнего магнитного поля и кванты этого поля γ + (м) и γ ‾(м) будут "переходить" на кольцевые Э.У.к. е− −ов и псевдо "е+ −ов", наделяя их реактивными импульсами. Напомню, что эти Э.У.к. "сверху" "атакуются" квантами магнитного поля γ ‾(м), а "снизу", квантами γ + (м).

А теперь, для определения направления действия Лоренцевых сил на подвижные е− − ны и псевдо "е+ −ны" в проводнике, нам следует определить направление движения γ + (м) и γ ‾(м) по их кольцевым Э.У.к.
В соответствии с правилом Левостороннего Буравчика (ПЛБ), данные направления движения определяются сторонним наблюдателем по отношению встречного или попутного потока квантов стороннего электрического поля в проводнике. Подобным же образом можно поступить и в случае с виртуальными потоками квантов γ + (в) и γ ‾(в) по отношению схемы рис. 18 /в (1)/ − (пр. Е и П −ия).
В данном примере, встречным виртуальным потоком для е− − ов является поток γ + (в) квантов. Поэтому, если мы будем исходить из условия, что этот поток удаляется от стороннего наблюдателя в направлении движущемуся ему навстречу проводника, то по отношению к наблюдателю эти кванты γ + (в), после прохода сквозь е− −ны проводимости и перехода на "свои" кольцевые Э.У.к., должны будут двигаться по ним против часовой стрелки, соответственно кванты γ ‾(в) из попутного потока, по "своим" Э.У.к. − по часовой (по отношению стороннего наблюдателя). В этих же направлениях будут двигаться и кванты из внешнего магнитного поля.
Реактивные импульсы, которые приобретут по отдельности кольцевые Э.У.к. подвижных электронов от γ + (м) и γ ‾(м) из внешнего магнитного поля, с учётом позонного эффекта в них, в проводнике будут направлены в одну сторону − слева − направо (по отношению стороннего наблюдателя) − см. рис. 18 в (1). Соответственно, Лоренцевы силы, обусловленные действием реактивных импульсов на кольцевые Э.У.к. электронов, вынудят Э.У.к., а следовательно, и электроны, по отношению стороннего наблюдателя двигаться в проводнике в направлении − справа − налево.

В случае с псевдо "е+ −ми", направление "действия реактивных импульсов" на их кольцевые Э.У.к. будет противоположным, нежели в случае с электронами. После "перехода" γ + (в) и γ ‾(в) на Э.У.к. псевдо позитронов, они, став квантами γ + (м) и γ ‾(м), по отношению стороннего наблюдателя будут обходить свои Э.У.к. в следующем направлении: γ + (м) по часовой стрелке, а γ ‾(м) против. В этих же направлениях будут двигаться и кванты γ + (м) и γ ‾(м) из внешнего магнитного поля, после "перехода" с его линий индукции на Э.У.к. псевдо позитронов.
Соответственно реактивные импульсы, приобретаемые этими Э.У.к., вынудят их, а следовательно, и псевдо позитроны, двигаться по проводнику в направлении слева направо, т. е. в противоположную сторону, нежели электроны /см. рис. 18 в (1)/. А так как их осевые О.Т. совпадают по направлению с направлением движения проводника в этом поле, то движение электронов и псевдо позитронов под действием Лоренцевых сил вдоль проводника будет осуществляться "боком" /см. рис. 18 в (1)/.

Двигающиеся под действием Лоренцевых сил е− −ны и псевдо "е+ −ны", будут скапливаться на противоположных концах (условного) проводника. В результате их накопления, в таком проводнике условно возникнет стороннее, кулоновское электрическое поле (примечание: напомню, что речь идет об условной модели проводника, в котором наряду с подвижными электронами (условно) присутствуют и подвижные псевдо позитроны; между собой они не взаимодействуют).
А так как материальной основой электрического поля являются кванты, то возникает вопрос: Какой природы должны быть кванты данного стороннего, кулоновского электрического поля? Ведь в проводнике квантов γ + (эл.) и γ −(эл.), являющиеся квантами внешнего электрического поля, нет. В то же время, как было показано в статье (1) − / см., например, рис. 21 и 22 в (1)/, движение отрицательных и положительных зарядов возможно только при наличии материальных носителей электрического поля. Если руководствоваться этим положением, то стороннее кулоновское поле в проводнике должно создавать соответствующие потоки квантов. И таковыми, согласно Квантовой теории поля, должны быть виртуальные кванты γ + (в) и γ −(в).

В первом приближении, подобные потоки схематично возникают следующим образом:
согласно Квантовой теории поля, электроны окружены "шубой" виртуальных квантов. Эта "шуба" во всех направлениях пронизывается силовыми линиями Л.П.эл. их электрического поля. По исходящим Л.П.эл. из электронов перемещаются кванты γ −(в) в направлении от них; по тем же Л.П.эл., которые входят в электрон, перемещаются кванты γ + (в). Получается, что потоки γ +(в) по "своим" Л.П.эл. идут к электрону, а потоки γ −(в) по "своим" Л.П.эл. от него.

Рассуждая подобным образом, невольно приходишь к мысли о функциональном предназначении электронов ( и тех же позитронов): они преобразуют зарядовую принадлежность квантов. Электроны из квантов γ + (в) "делают" γ −(в), а позитроны из квантов γ −(в) "делают" γ + (в).

По Л.П.эл., исходящим из электронов и ориентированных в направлении проводника, кванты γ −(в) "стекают" в проводник и движутся по нему к противоположному его концу. Тоже происходит с квантами γ + (в), "стекающих" в направлении проводника с псевдо позитронов. Тем самым в проводнике возникают два противоположных потока виртуальных квантов. Эти потоки, см. рис. 21 в (1), взаимодействуют с Л.П.эл. электрического поля подвижных электронов и тем самым препятствуют продвижению электронов под действием лоренцевых сил, т. к. их действие противоположно действию первых.
То есть в проводнике возникает "противоборство" магнитного и электрического полей. Со стороны внешнего магнитного поля в этом "противоборстве" (образно) участвуют Э.У.к. электронов, а со стороны электрического поля Л.П.эл. Схематично подобную картину "противоборства" можно видеть на схематичном рис. 17 в (1) − (примечание: так как речь идёт о виртуальных квантах, то следует иметь в виду, что на этой схеме вместо квантов γ + (эл.) и γ −(эл.) должны быть кванты γ + (в) и γ −(в)).



Подчеркну ещё раз, что "движение" электронов и псевдо позитронов в условном проводнике, движущемуся через стационарное однородное магнитное поле, будет осуществляться не как обычно, когда встречным потоком для первых является поток квантов γ + (в), а для вторых γ −(в), а тем, что они (образно) меняются встречными потоками квантов. Электроны в таком проводнике "движутся" навстречу потоку квантов γ −(в), а псевдо позитроны потоку квантов γ +(в).

По поводу методики, применённой при анализе функциональной схемы данного примера е − движения прямолинейного проводника в стационарном однородном магнитном поле, со стороны Читателя правомерен следующий вопрос: "А правомерно ли в данной методике использование виртуальных квантов ?"
Вот теперь, когда события в функциональной схеме /см. рис. 18 в (1)/ рассмотрены с причинных позиций, без использования правила правой руки, правомерно поставить следующий вопрос: "А действительно ли в проводнике, движущемуся сквозь внешнее магнитное поле, возникает стороннее электрическое поле? Ведь основой любого электрического поля являются кванты γ + (эл) и γ −(эл), выполняющих роль переносчиков электрического взаимодействия!"
А что же есть в наличии? Есть только кванты γ + (м) и γ −(м) внешнего магнитного поля и кольцевые Э.У.к. электронов (да условных псевдо позитронов). Ведь только за счёт приобретения ими реактивных импульсов от этих квантов и происходит разделение носителей "электрических" зарядов. Как это происходит было показано выше. А возникновение кулоновского поля в проводнике − это уже следственная сторона "работы", производимой квантами γ + (м) и γ −(м) из внешнего магнитного поля над кольцевыми Э.У.к. электронов (псевдо позитронов).
Следовательно, исходя из проделанного анализа функциональной электромагнитной, условной схемы движения проводника во внешнем однородном магнитном поле, можно сделать однозначный вывод: в Природе как такового электрического поля, которое изначально было интерпретировано как стороннее, не существует, так же как не существует и обезличенных электрических зарядов + −с и − −с! Эти условные понятия, необходимо было ввести в обиход, чтобы хоть как−то объяснить наблюдаемые события в электромагнитных схемах подобного вида. При более углубленном понимании электромагнитного явления, эти искусственные понятия "наполняются" причинным содержанием. При этом сторонний наблюдатель (образно) из "лагеря" со следственной основой "переходит в лагерь с причинной".
Подобные рассуждения приводят к мысли о том, что в проводнике, движущемуся сквозь магнитное поле, электроны и псевдо позитроны находятся под воздействием и внешнего магнитного поля, и под воздействием, но не стороннего, а внутреннего электрического поля, которое возникает как побочный результат в момент "движения" электронов и псевдо позитронов под действием Лоренцевых сил.

Если же теперь мы от этой условной схемы перейдём к схеме движения электронов в проводниках 1 −го рода, то при наличии кольцеобразно замкнутого контура, в той его части, которая движется сквозь внешнее магнитное поле, подвижные электроны под действием Лоренцевых сил будут двигаться "боком". А на участке не подверженному внешнему магнитному полю, будут двигаться обычно, как и в случае их движения под действием внешнего электрического поля, "прикладываемого" к проводнику. Но при этом их движение будет обусловлено не за счёт потоков γ + (эл) и γ −(эл) − таковых в контуре нет, ибо в нём нет внешнего электрического поля, а за счёт того, что подвижные электроны, проталкивающиеся Лоренцевыми силами, будут "толкать" и остальные электроны в остальной части замкнутого контура. То есть Лоренцевы силы (образно) выполняют роль толкача электронов в замкнутом проволочном контуре и это "проталкивание", исходя из пр. Е и П −ия, можно уподобить подвижному железнодорожному составу, который подаётся тепловозом или электровозом на горку для его расформирования.

Движение подвижных электронов в замкнутом проволочном контуре под действием Лоренцевых сил и под действием внутреннего, стороннего электрического поля, возникающем в проводнике, взаимно противоположно. На участке, где действуют силы Лоренца, электроны движутся против внутреннего электрического поля, на остальном же как и обычно. Магнитное поле вокруг такого внешнего участка будет подобно магнитному полю прямолинейного тока, но по его Э.У.к. будут двигаться не кванты γ (м), а кванты γ (в). Другими словами: на участке, где действуют силы Лоренца электроны будут двигаться от + −са к − −су, а на внешнем участке как и обычно от − −са к + −су.


7.2. Вращение проволочного витка (прямоугольной рамки) в однородном
стационарном магнитном поле.

Характерной особенностью примеров, рассмотренного в разделе 7. /см. также п.7. в (1) /, было то, что Э.Д.С. в проводнике не меняла своего направления. Если же Э.Д.С. с течением времени периодически меняет своё направление, то в проводнике создаётся переменная Э.Д.С. Прежде чем мы перейдём к рассмотрению причинного механизма возникновения переменной Э.Д.С., обратимся к "Элементарному учебнику по физике" под ред. акад. Г.С.Ландсберга , т. 2, М., 1966г., см. ј152, стр.152, стр. 360 ? 364, в котором даётся объяснение механизма возникновения переменной Э.Д.С. на примере вращения проволочного витка в магнитном поле.

"...Между полюсами сильного магнита NS, т. е. в магнитном поле (см. рис.92), вращается проволочный виток, концы которого припаяны к кольцам А и В, вращающимся вместе с рамкой; к этим кольцам прижимаются пружинные пластины Р и Q (так называемые щ ё т к и), от которых идут провода к внешней цепи. При вращении витка в магнитном поле пронизывающий его магнитный поток всё время изменяется, и следовательно, в витке возникает индуцированная Э.Д.С.





... Рассмотрим теперь несколько подробнее, какова будет возникающая в нашем витке индуцированная Э.Д.С. Для простоты будем считать магнитное поле, в котором вращается рамка, однородным. Магнитный поток через наш виток Ф, как мы знаем, есть произведение напряжённости магнитного поля Н на площадь витка S и на синус угла Φ между плоскостью витка и направлением поля:
Ф = Н • S • sin Φ.

Если виток вращается р а в н о м е р н о и совершает полный оборот за время Т, то за одну секунду наша рамка поворачивается на угол 2π/Т радианов. Поэтому, если мы будем время отсчитывать от того момента, когда наша рамка стояла параллельно линиям поля, то значение угла Φ в некоторый момент времени t будет равно Φ = 2πt/Т. Обозначая частоту вращения рамки, т. е. число её оборотов в секунду буквой ƒ, а угловую скорость буквой ω, мы можем написать, что
ƒ = 1/Т и ω = 2 π ƒ = 2 π / Т.

Стало быть, Φ = ω t.

Поставив это выражение в формулу для величины магнитного потока, мы увидим, что закон его изменения с течением времени имеет вид:

Ф = Н • S • sin ωt .

График, изображающий зависимость магнитного потока через наш виток от времени, представляет собой, следовательно, с и н у с о и д у (см. рис. 91а).


Магнитный поток меняет свой знак, как мы видим, два раза за каждый оборот рамки, обращаясь в н у л ь в те моменты, когда она параллельна направлению поля, и достигая м а к с и м а л ь н ы х значений (того или иного знака) в моменты, когда она п е р п е н д и к у л я р н а к полю.
Индуцируемая в рамке Э.Д.С. определяется не значением самого магнитного потока, а скоростью его изменения, т. е. величиной ΔФ/Δt. Нетрудно видеть, что и эта величина не остаётся постоянной, а всё время изменяется при вращении рамки. На рисунке 91а показаны значения изменения магнитного потока ΔФ за одинаковые промежутки времени Δt для момента t = 0, когда Ф = 0, и для момента около t = Т/4. Первое значение ΔФ гораздо больше второго, и следовательно, мгновенное значение индуцированной Э.Д.С. в момент t = 0 имеет максимальное значение, а по мере вращения рамки убывает, достигая значения нуль к моменту Т/4. При дальнейшем повороте рамки Э.Д.С. меняет свой знак. Действительно, по правилу Ленца индуцированная Э.Д.С. всегда направлена так, чтобы магнитное поле создаваемого ею тока тормозило процесс, вызывающий индукцию. Поэтому в течение первой четверти периода, когда магнитный поток через рамку в о з р а с т а е т, поле индукционного тока должно о с л а б л я т ь внешнее поле Н, а в течение следующей четверти периода, когда магнитное поле у б ы в а е т, оно должно у с и л и в а т ь это поле. Отсюда ясно, что в моменты прохождения Э.Д.С. через нуль должно происходить изменение её знака."

Итак, по данной выдержке из учебника Г.С.Ландсберга отметим основное: в ней отсутствуют основные участники данного опыта е− электроны проводимости, кванты γ + (м) и γ −(м) из внешнего магнитного поля, и виртуальные − кванты γ + (в) и γ − −(в). Попробуем объяснение данного опыта провести с их учётом. И в первую очередь выделим основные составляющие этого опыта, которые в течение поворота рамки на угол 2π остаются всё время постоянными. К ним следует отнести площадь рамки и магнитный поток между полюсами магнита. Постоянство последнего обусловлено наличием в схеме постоянного магнита. Это означает, что плотность двух взаимно встречных потоков γ + (м) и γ −(м) магнитного поля между полюсами магнита остаётся постоянной во времени и не зависит от угла поворота рамки. То есть в единицу времени, через контрольное сечение, например, в 1 кв. см., в обоих направлениях "проходит" одинаковое количество квантов обоих видов. К переменным составляющим этого опыта следует отнести время оборота рамки, а также угол её поворота Φ.

Оперируя этими составляющими, учёные посредством соответствующих формул смогли увязать последовательность событий в этом опыте. Так, например, когда рамка с проволочным витком располагается параллельно линиям индукции магнитного поля и время принимается равным нулю, то предполагается, что и магнитный поток Ф тоже равен нулю. Но ведь на самом деле магнитный поток постоянен и нулю никак равняться не может. В то же время, в этом положении рамки, мгновенное значение индуцированной Э.Д.С. достигает максимальное значение.
Если исходить из этих соображений, то налицо явное несоответствие. Подобное несоответствие было устранено посредством введения в обиход изменяющейся величины − "обезличенного" магнитного потока в единицу времени. Было условно принято, что площадь контура рамки в положении параллельном линиям индукции магнитного поля, т. е. когда t = 0, равна нулю и только, когда рамка занимала положение перпендикулярное линиям магнитной индукции, через время t = Т/4, считалось, что магнитный поток Ф возрастал до максимума, но в противоположность ему, мгновенное значение Э.Д.С. электромагнитной индукции почему−то обращалось в нуль.
При последующем повороте рамки, Э.Д.С. меняет свой знак и через время t = Т/4 вновь возрастает до максимума, а вот магнитный поток при наличии однородности и постоянства магнитного поля (Н = const), то же обращается в нуль.
К сказанному следует добавить и другое соображение: в прямоугольной рамке, находящейся под воздействием магнитного потока внешнего магнитного поля, т. е. потоков квантов γ + (м) и γ −(м), находится не вся её площадь, а только два её проволочных участка, в которых и возникает индукционный ток. Остальная же её площадь, в деле возникновения индукционного тока в контуре, участия не принимает. Спрашивается: "Правомерно ли в формуле величины магнитного потока учитывать всю её площадь?"

Исходя из этих соображений, можно в первом приближении утверждать, что устоявшаяся точка зрения в отношении взаимосвязи между магнитным потоком и Э.Д.С. индукции, изначально носила чисто наблюдательный характер и в своей основе исключала её причинное объяснение.

Ну что же, попробуем и этот опыт объяснить с позиции причины, использовав для этого вышеизложенную методику антиподно−эквивалентного подхода к причинной стороне электромагнитных явлений. И первое, что предстоит нам сделать, это определить пространственное положение кольцевых Э.У.к. подвижных электронов в тот момент, когда рамка (проволочный виток) располагается параллельно линиям индукции магнитного поля постоянного магнита, т. е. когда t = 0, и в момент, когда рамка повернётся на угол Φ = 90° . В этом положении рамка перпендикулярна линиям индукции внешнего магнитного поля − /примечание: магнитное поле электрона структурно состоит из двух составляющих − меридиональной и экваториальной; схематично это показано на рис. 27.1 и 27.2 в (1). Первая обусловливает ориентацию е− −на (е+ −на) при его движении в магнитных и электрических полях; вторая обуславливает перпендикулярное их смещение относительно направления их движения в пространстве магнитных полей. Их совместная схематичная прорисовка представляет определённую трудность. Поэтому там, где главенствующая роль принадлежит первой, на условной схеме рисунка отдельно показана только меридиональная составляющая − см., например, рис. 1; 2 и 23 в (1); а в случае второй, экваториальной, отдельно показаны только Э.У.к. − см., например, условные рис. 12; 13; 14 и 18 в (1)./ Сказанное в этом примечании имеет непосредственное отношение и рис.93 в этой статье.

Итак, когда рамка при вращении занимает положение параллельно линиям индукции внешнего магнитного поля, т. е. когда условное время t = 0 (см. рис. 93), то в этот момент вектор скорости Vлк участка ЛК проволочного контура, а следовательно, и подвижных в нём электронов Vе−, по отношению к рамке направлены вверх (см. рис. 93), а на участке СД наоборот, вниз (примечание: рамка вращается по часовой стрелке). А так как оси вращения электронов проводимости совпадают с направлением вектора их скорости Vе− , то при прохождении рамкой горизонтального положения, кольцевые Э.У.к. электронов должны (условно) располагаться в плоскостях, которые параллельны линиям индукции внешнего магнитного поля и плоскости самой рамки.
Такая их ориентация обусловливается воздействием на электроны двух потоков виртуальных квантов γ + (в) и γ −(в) из окружающего контур пространства. Направление этих потоков всегда совпадает с направлением вектора скорости Vе− , перемещающихся в пространстве е− −ов (е+ −ов и т.д. − пр. Е и П −ия!) − примечание: на рисунке 93 прорисована только одна, экваториальная составляющая магнитного поля электронов; другая, меридиональная, отсутствует. Не показаны также и Л.П.эл. их электрического поля.




Рис. 93. Условная, функциональная схема вращения проволочного,
прямоугольного витка в однородном магнитном поле.

Следует также отметить, что в процессе вращения рамки, вектора окружной скорости участков ЛК и СД по отношению друг друга хотя и разнонаправлены, но по отношению плоскости рамки, в процессе её вращения, сохраняют постоянный угол, равный 90° . Это же относится и к плоскостям, в которых условно располагаются кольцевые Э.У.к подвижных электронов.
При таком положении этих условных плоскостей относительно плоскости рамки, кольцевые Э.У.к. электронов будут располагаться не перпендикулярно участкам ЛК и СД, а вдоль этих участков, образуя (условно) слой толщиной, равный диаметру проволоки.
При прохождении рамкой горизонтального положения, кольцевые Э.У.к электронов проводимости обоих участков проволочного контура пересекают линии индукции магнитного поля под углом Φ = 90° . В этом положении, как было показано выше, в системе кольцевых Э.У.к. электронов наличествует максимальный позонный эффект, частично экранирующий соответствующие участки этих Э.У.к. от потока квантов γ + (м) или γ −(м). Это приводит к тому, что кольцевые Э.У.к. электронов проводимости подвержены эффективному реактивному действию квантов γ + (м) и γ −(м) из внешнего магнитного поля не по всей длине окружности, а только частично. При этом наименьшая длина позонных участков Э.У.к., подвергающихся эффективному, а вернее раздельному реактивному воздействию со стороны этих квантов, приходится как раз на то положение рамки, когда она параллельна вектору индукции магнитного поля В или линиям его индукции (см. условный рис. 93), где от каждой системы взаимно встречных кольцевых Э.У.к. электронов показано по два кольца; то же самое мы имеем и в случае рисунка 7 а и б, см. в (1), сектора 1 и Ш.

Теперь, чтобы определить направление "обхода" квантами γ + (м) и γ −(м) кольцевых Э.У.к. электронов в участках ЛК и СД проволочного контура, после перехода этих квантов с линий индукции магнитного поля на Э.У.к. электронов, воспользуемся правилом Левостороннего Буравчика. Для этого воспользуемся квантами γ + (в) и γ −(в), под воздействием которых находятся подвижные электроны участков ЛК и СД при вращении рамки.
Для электронов участка ЛК, движущимся (условно) снизу − вверх, из положения ам в положение бг, встречным потоком будет поток квантов γ + (в), а попутным поток γ −(в). Первый действует на электроны этого участка "сверху", а второй "снизу". Поэтому, если смотреть с конца вектора скорости электронов Vе− данного участка в направлении на Э.У.к., то кванты γ + (в), после того как они окажутся на "своих" Э.У.к., будут двигаться по ним против часовой стрелки, а кванты γ −(в), соответственно, по часовой (см. рисунок 93). В этих же направлениях будут перемещаться и кванты γ + (м) и γ −(м), после того, как они с линий индукции магнитного поля "перебазируются" на "свои" кольцевые Э.У.к. в электронах участка ЛК.
Наличие позонного эффекта в системе кольцевых Э.У.к. у электронов участка ЛК приведёт к тому, что участки Э.У.к., которые находятся под реактивным воздействием только квантов γ −(м), будут двигаться вдоль этого проволочного участка в направлении от точки К к точке Л. Тоже будет происходить и с участками кольцевых Э.У.к., которые находятся под реактивным воздействием квантов γ + (м). Они будут двигаться вдоль проволочного участка ЛК тоже в направлении от точки К к точке Л.

Совместное действие реактивных сил на антиподных участках Э.У.к, направленных в одну сторону, через их посредство передадутся электронам и они по участку ЛК будут двигаться от точки К к точке Л. Реактивные силы в данном случае являют собой ни что иное, как силы Лоренца, а наличие в системе кольцевых Э.У.к. максимального, экранирующего эффекта и приводит к тому, что в этом положении рамки (в горизонтальном), эти силы максимальны, а следовательно, и максимально мгновенное значение индуцированной Э.Д.С. в данный момент времени. В соответствии же с бытующим на данный момент правилом, индукционный ток на участке ЛК будет иметь направление от точки Л к точке К. То есть такое же, как если бы его направление мы определяли, руководствуясь правилом правой руки.

На проволочном участке СД будут происходить противоположные события, нежели на участке ЛК. Это мотивируется тем, что вектор скорости участка СД, по отношению вектора скорости участка ЛК направлен в противоположную сторону, ибо данный участок контура движется по нисходящему участку кольцевой траектории − из положения бг, в положение ам, т. е. (условно) сверху − вниз.
Используя методику определения движения квантов γ + (в) и γ −(в) по кольцевым Э.У.к. электронов проводимости данного участка, мы установим, что под действием сил Лоренца электроны по нему будут двигаться в направлении от точки С к точке Д, т. е. в противоположном направлении, нежели на участке ЛК. При этом изменение мгновенного значения индуцированной Э.Д.С. в данном участке контура будет такое же, как и на участке ЛК и по отношению друг друга они будут протекать в фазовом режиме. При наличии замкнутости проволочного контура, по нему будет идти ток, наличие которого зафиксирует гальванометр, включённый в цепь.

Теперь осталось выяснить причину убывания (изменения) мгновенного значения индуцируемой Э.Д.С. при "переходе" рамки из положения с t = 0 (из горизонтального) в положение t = Т/4 (в вертикальное), т. е. когда она ориентируется к линиям индукции внешнего магнитного поля под углом 90° . Как следует из опыта, при таком её положении мгновенное значение индуцируемой в участках ЛК и СД Э.Д.С. равно нулю.

Причина изменения мгновенного значения индуцируемой Э.Д.С. состоит в следующем:
при вращении рамки, вектора окружной скорости участков ЛК и СД должны постоянно располагаться вдоль касательной к условной окружности, по которой движутся в пространстве эти участки. Это приводит к тому, что данные вектора при вращении рамки как бы поворачиваются в пространстве и через время t = Т/4, когда она займёт положение, перпендикулярное линиям индукции магнитного поля, они займут положение, параллельное этим линиям.
Но одновременно, с поворотом векторов окружной скорости участков ЛК и СД, также поворачиваются и оси вращения подвижных электронов под действием потоков виртуальных квантов γ + (в) и γ −(в). В результате условные плоскости с кольцевыми Э.У.к. подвижных электронов, через время поворота рамки t = Т/4, занимают положение, перпендикулярное вектору В магнитной индукции внешнего магнитного поля или другими словами, располагаются под углом 90° к линиям его индукции.
Но ранее /см. рис. 8 в (1)/ было показано, что в этом положении кольцевые Э.У.к. электронов "атакуются" квантами γ + (м) и γ −(м) по всей длине окружности − см. также рис. 93. В результате возникают условия, когда реактивные импульсы от этих квантов в системе антиподных Э.У.к каждого электрона компенсируют друг друга. Это приводит к тому, что суммарная сила Лоренца становятся равной нулю и движение подвижных электронов по участкам ЛК и СД в этом положении рамки прекращается. При этом особо следует подчеркнуть, что силы Лоренца в системах антиподных Э.У.к. каждого подвижного электрона не исчезают. Они как присутствовали в них, так и "остаются", а вот позонный эффект в отношении квантов γ + (м) и γ −(м) во внешней структуре электронов или в экваториальной составляющей его магнитного поля, перестаёт действовать.
С проходом рамкой вертикального положения, система направленности движения индукционных токов по участкам ЛК и СД оборачивается в Пространстве и во Времени. Участок СД будет двигаться по восходящей кольцевой траектории − от ам к бг, а ЛК по нисходящей − от бг к ам. Теперь всё, что было выше сказано в отношении участка ЛК, будет относится к участку СД, а в отношении участка СД, к участку ЛК.
Подобная "оборачиваемость" направления индукционных токов в рамке, в момент прохождения ею вертикального положения, происходит в ней дважды за её один, полный оборот. Также в фазе с током, происходит и изменение направления индуцируемой Э.Д.С. на участках ЛК и СД.

В отношении тех участков траектории рамки, на которых кольцевые Э.У.к. электронов проводимости пересекают линии индукции магнитного поля под углом Φ > 0, но < 90° можно сказать следующее:
при переходе рамки из вертикального положения в горизонтальное, например, когда участок ЛК проволочного контура движется по восходящей кольцевой траектории, т. е. от ам к бг, вектор его окружной скорости, совпадая по направлению с касательной к условной окружности, по отношению линий индукции внешнего магнитного поля всё время "поворачивается" в пространстве. Угол Φ , под которым он "атакует" данные линии, изменяется от 0 −ля до 90° . Но одновременно, с "поворотом" данного вектора, также поворачиваются и условные плоскости с кольцевыми Э.У.к. подвижных электронов. При этом угол их "атаки" линий индукции внешнего магнитного, тоже изменяется от 0 −ля до 90° .
В результате степень эффективной реактивной "загрузки" кольцевых Э.У.к. подвижных электронов квантами γ + (м) и γ −(м) меняется. Из "максимальной", когда эти Э.У.к. данными квантами "загружены" частично по длине их окружности, т. е. когда угол Φ = 0, она становится минимально эффективной при угле Φ = 90° . Подобная изменчивость обусловлена всё тем же эффектом экранизации квантов γ + (м) и γ −(м) во внешней структуре подвижных электронов самими же кольцевыми Э.У.к., которые, исходя из антиподности, между собой являются антиподами /см. например, условный рисунок 7 а и б в (1)/. При угле Φ = 90° эффект позонной экранизации перестаёт действовать в антиподных Э.У.к. электронов.

Подобная ситуация напрямую отражается и на суммарных Лоренцевых силах, действующих в антиподных системах кольцевых Э.У.к. каждого электрона. Эти силы, при переходе рамки из вертикального положения в горизонтальное, когда участок ЛК движется по восходящей круговой траектории, как бы "расщепляются". Одна половина сил, например, от квантов γ −(м), задействует только свои Э.У.к. − см. тот же рис. 17 а и б в (1), а другая половина, от квантов γ + (м), тоже свои Э.У.к., но антиподные первым (см. рис. 93).
Эффект экранизации этих квантов из внешнего магнитного поля антиподными Э.У.к электронов и является той причиной, в результате которой, при переходе рамки из вертикального положения в горизонтальное, в системе антиподных Э.У.к. каждого электрона, суммарная Лоренцева сила "распадается" на составные части. Эти части, в течение 1/4 периода поворота рамки, к моменту, когда угол Φ достигает 90° (примечание: в этот момент рамка занимает горизонтальное положение), возрастают от 0 −ля до определённого максимума. Такие же события, одновременно происходят и с электронами проводимости участка СД, только на нём Лоренцевы силы воздействуют на электроны противоположно, нежели на участке ЛК.
При дальнейшем повороте рамки, когда угол Φ. изменяется от 90° до 0 −ля, Лоренцевы силы на участке ЛК проволочного контура тоже претерпевают изменения. Соответственно, также изменяется и мгновенное значение индуцируемой Э.Д.С. на этом участке. То есть четверть периода, когда рамка переходит из вертикального положения в горизонтальное, Э.Д.С. возрастает от 0 −ля до некоторого максимума, а в последующую четверть периода, когда рамка из горизонтального положения переходит в вертикальное, она убывает от максимума до 0 −ля.
В дальнейшем, когда рамка (образно) проходит через вертикальное положение, участок проволочного контура ЛК начинает движение по нисходящей круговой траектории. Вектор его окружной скорости, постепенно "оборачиваясь" в пространстве, движется вниз. Одновременно, под действием потоков γ + (в) и γ −(в) поворачиваются и оси вращения подвижных электронов этого участка, а вместе с ними и условные плоскости с кольцевыми Э.У.к.

На протяжении сего времени движения по нисходящей круговой траектории, последовательность событий в участке ЛК проволочного контура будет такой же, когда он двигался изначально по восходящей круговой траектории, но их пространственная направленность будет уже противоположной в виду того, что кольцевые Э.У.к. подвижных электронов, по отношению к положению на восходящем участке круговой траектории, обернутся на 180°. В результате на 180° меняется и направленность реактивной "загрузки" участков Э.У.к. квантами γ + (м) и γ −(м) и, как следствие, на 180° меняется пространственная направленность Лоренцевых сил.
Если на участке ЛК, в момент его движения по восходящей круговой траектории, электроны, под действием Лоренцевых сил двигались от точки К к точке Л, то при движении этого же участка по нисходящей круговой траектории, электроны под действием Лоренцевых сил будут двигаться уже в противоположном направлении, т. е. от точки Л к точке К. Сказанное в отношении проволочного участка ЛК следует отнести и к участку СД, только движение электронов проводимости будет происходить не от точки С к Д, а от Д к С.

Периодически, через половину периода оборота рамки, участки ЛК и СД меняются местами на круговой траектории. Это приводит к тому, что одну половину периода электроны проводимости, под действием Лоренцевых сил, движутся то в одном направлении, а в другую, в противоположном. В результате работа, "производимая" Лоренцевыми силами или Э.Д.С. электромагнитной индукции по разделению зарядов на участках, полпериода действует то в одном направлении, то в другом. И причина изменения знака Э.Д.С. исходит не из−за того, что магнитное поле индукционного тока, согласно правила Ленца деструктивно или созидательно воздействует на внешнее магнитное поле постоянного магнита, а из−за того, что при вращении проволочного витка в этом поле, Э.У.к. электронов периодически "загружаются" квантами этого поля то частично, то полностью.

На вращение рамки в постоянном стационарном магнитном поле можно посмотреть и иначе: пусть электроны пространственно движутся в условной плоскости по траектории, совпадающей с рамочным контуром. Плоскость, в которой движутся в пространстве (условно) электроны, не меняет своего положения относительно потоков γ (м) внешнего магнитного поля и в одном случае, она параллельна вектору его магнитной индукции, а в другом, перпендикулярна ему. То есть она располагается или вертикально и угол Φ = 90° , или горизонтально и Φ = 0° . При этом её положении ЭДС электромагнитной индукции максимальна, а при Φ = 90° минимальна, т. е. равна нулю.
Рамка при вращении последовательно проходит через эти положения и не в состоянии самостоятельно воздействовать на ЭДС электромагнитной индукции. При таком раздельном взгляде на составные части опыта и получается, что рамка вращается сама по себе, а ЭДС "существует" сама по себе. То есть индукционный ток в рамке отсутствует и тем самым исключается его воздействие на внешнее, стационарное магнитное поле. Сторонний наблюдатель лишь отмечает положения рамки, в которых Э.Д.С. должна бала бы быть максимальна или минимальна.
К этому соображению можно добавить и другое: внешнее магнитное поле будет испытывать противодействие со стороны магнитного поля индукционного тока только в том случае, если плоскости Э.У.к. подвижных электронов от индукционного тока в проводнике будут параллельны линиям магнитной индукции внешнего магнитного поля, а сами однотипные линии по направленности в пространстве будут взаимно встречны.
При вращении же в нём рамки, они с этими линиями пересекаются под углом большими нуля или равным 90° . В результате и получается, что индукционный ток в рамке своим магнитным полем (подчеркнём − экваториальной составляющей магнитного поля подвижных электронов) не в состоянии оказать противоположное (деструктивное) воздействие на вешнее магнитное поле.

То есть направление индукционного тока в проволочном контуре, хотя и зависит от направления Э.Д.С., но сам ток своим магнитным полем не оказывает влияние на внешнее магнитное поле. Ведь согласно вышеизложенного, Э.Д.С. в контуре возникает не за счёт того, что магнитный поток под тем или иным углом пронизывает всю площадь рамки, а за счёт того, что в процессе её вращения под разным углом кванты γ + (м) и γ −(м) "атакуют" кольцевые Э.У.к. электронов. А это, при наличии в них позонного эффекта, действующего в системе антиподных Э.У.к. каждого электрона в отношении данных квантов, влияет на степень загруженности Э.У.к. Лоренцевыми силами.
При повороте рамки, длина кольцевых участков, на которых эффективно сказывается действие данных сил, меняется от нуля до максимума и от максимума до нуля. Подобные изменения происходят в течение каждого полупериода оборота рамки. В результате изменяются и Лоренцевы силы от нуля до максимума и от максимума до нуля.
А так как рамка вращается, то движение участков ЛК и СД можно уподобить возвратно поступательному движению отрезка проводника в том же однородном стационарном магнитном поле для случая, когда угол между вектором индукции В и вектором скорости проводника V составляет 90° . При таком движении, индуцируемая в проводнике Э.Д.С. всякий раз будет менять своё направление, что соответствующим образом отразится и на направлении движения электронов проводимости.
При наличии внешней цепи, по ней будет идти ток, который будет менять своё направление каждый раз, как только будет меняться направление движения проводника, а следовательно, и направление Э.Д.С. Но при этом напряжённость магнитного поля, а следовательно, и поток магнитной индукции, пронизывающий только участок подобного контура, будут постоянны во времени. Ведь в подобном примере не содержится площади контура, подверженного действию магнитного поля, ибо в этом случае его площадь будет равна произведению длины проводника на его диаметр.

Но тогда возникает вопрос: "Почему при определении Э.Д.С., когда рамка вращается, следует обязательно учитывать площадь контура?"

Ответ: При движении отрезка проводника в магнитном поле, он одновременно каналируется потоками квантов (фотонов) от магнитного поля и потоками виртуальных квантов из окружающего его пространства. Направление первых, т. е. γ + (м) и γ −(м), строго фиксировано взаимным расположением полюсов магнита, а вторых, зависит от направления его движения в пространстве, в котором, исходя из-за его изотропности, нет выделенных направлений. То есть плотность потоков виртуальных квантов (фотонов) одинакова в пределах телесного угла 4 π во всех направлениях.
В случае неподвижного проводника, находящиеся в нём электроны проводимости, "атакуются" со всех сторон квантами γ + (в) и γ −(в) одинаково. Следствием этого является то, что в проводнике они произвольно ориентированы. Произвольная их ориентация обусловлена произвольной направленностью суммарного ориентирующего момента каждого электрона, который возникает в системе меридиональных Л.П.м. от взаимодействия с виртуальными квантами.
Но принудительная ориентация моментов тот час возникает, как только проводник начинает двигаться в пространстве. С началом его движения, плотность потоков виртуальных квантов по направлению вектора скорости проводника возрастает. В результате меридиональные Л.П.м. /см. рис. 1а и б в (1)/ получают реактивных импульсов больше по направлению движения, нежели в каком−либо другом. Оси вращения электронов проводимости разворачиваются и занимают положение, совпадающее с направлением вектора скорости проводника (материального тела).
В результате плоскости кольцевых Э.У.к. электронов ориентируются перпендикулярно вектору их скорости и в таком положении пересекают линии индукции внешнего магнитного поля. В случае же произвольной ориентации электронов, при неподвижном проводнике, плоскости кольцевых их Э.У.к по отношению потоков γ + (м) и γ −(м) тоже произвольно ориентированы. В результате под действием реактивных импульсов или Лоренцевых сил, получаемых кольцевыми Э.У.к. от этих квантов, электроны проводимости в объеме проводника движутся хаотично. Когда же проводник движется, то их движение осуществляется согласованно, в одном направлении, ибо в одном направлении действуют силы Лоренца в системе Э.У.к. подвижных электронов.

Подобное, в соответствии с пр. Е и П −ия, должно иметь место во всех случаях, буд−то заряженное тело (см. −, опыт Г.Роуланда и А.А.Эйхенвальда в Москве в 7.1.) или просто проводник; тоже и в случае с "элементарными" частицами.
То есть, внешнее магнитное поле на "заряженное" тело или просто заряд действует только в случае, когда по отношению поля соответствующим образом ориентируются кольцевые Э.У.к. электронов или ионов, содержащихся в заряженном теле. Но необходимая ориентация Э.У.к. возникает только с началом движения заряженных тел или зарядов в пространстве. До этого момента, при произвольной ориентации электронов и ионов по отношению друг друга, результат от воздействия внешнего на них магнитного поля равен нулю, ибо Лоренцевы силы от каждого электрона (иона) в сумме равны нулю.

Исходя из вышесказанного можно предполагать, что согласованное действие Лоренцевых сил на заряды проявляется только тогда, когда они начинают двигаться в пространстве в том или ином направлении. С момента движения заряда, в пространстве "возникает" выделенное направление, которое характеризуется повышенной плотностью соответствующих, взаимовстречных потоков и таковыми являются потоки различных "элементарных", а также и виртуальных частиц, фотонов света, гравитонов (пр. Е и П −ия) −, о последних речь будет идти в отдельной статье "Гравитация".

В качестве примера проанализируем движение в пространстве двух неподвижных относительно друг друга электронов, которые при наличии у них одинаковых, одноимённых зарядов, вместо того чтобы отталкиваться, они по непонятной причине, наоборот, притягиваются. Подобное поведение в пространстве двух электронов подобно их движению в двух параллельных проводниках / см. условный рис. 11 и 12 в (1)/.
В обоих примерах, что и в случае параллельных проводников /рис. 11 в (1)/, что и в случае движения спаренных электронов в пространстве, возникает у каждого электрона собственное экваториальное магнитное поле. Этими полями и взаимодействуют электроны. Схематично подобное взаимодействие осуществляется при наличии соответствующих посредников: в случае схемы рис. 12 в (1) это кванты γ + (эл) и γ −(эл), которые после переориентации их электронами переходят на их кольцевые Э.У.к. и становятся квантами γ + (м) и γ −(м); в случае же летящих в пространстве двух, относительно друг друга неподвижных электронов, это кванты γ + (в) и γ −(в), которые из разряда виртуальных переводятся электронами в γ + (м) и γ −(м) на свои кольцевые Э.У.к.
При наличии "наложения" кольцевых Э.У.к. обоих электронов друг на друга происходит переход (перескакивание) квантов γ(м) от одного электрона к другому. Схематично этот переход показан на рис. 12а в (1). Э.У.к. электронов получают от квантов γ(м) соответствующие реактивные импульсы, в результате чего первые начинают перемещаться относительно друг друга. А так как Э.У.к. жёстко связаны с внутренней структурой электрона (с его ядром), то это движение передаётся самим электронам и они притягиваются. То есть притяжение идёт за счёт магнитных сил, которые в данных примерах превосходят электрические силы отталкивания. По характеру действия эти силы можно уподобить Лоренцевым силам.

Но вернёмся к вопросу о площади контура рамки. Обратимся вновь к рис. 7 а и б в (1).
При функциональном анализе обоих рисунков мы исходили из условия, что кольцевые Э.У.к. подвижных электронов изымают из окружающего их пространства кванты внешнего магнитного поля. То есть исходили из того, что Природой на Э.У.к. как бы "возложена" функция обходных путей.
Но за движение по этим путям (направлениям), квантам γ + (м) и γ −(м) приходится (образно) "расплачиваться" реактивными импульсами, под действием которых Э.У.к. , а следовательно, и электроны проводимости приводятся в движение. Это движение передаётся проводнику и в зависимости от направления движения в нём потоков γ + (эл) и γ −(эл) из внешнего электрического поля, прикладываемого к нему, он смещается в том или ином направлении между полюсами магнита. Сам проводник в это время располагается под углом 90° к линиям индукции внешнего магнитного поля /см. рис. 6 в (1)/.
В последующем кванты γ + (м) и γ −(м), двигаясь вдоль Э.У.к, проходят определённый этап в своём развитии и по его завершении переводятся подвижными электронами в потоки внешнего электрического поля, прикладываемого к проводнику. То есть они просто−напросто "изымаются" подвижными электронами со своих, антиподных кольцевых Э.У.к и переводятся во внутрь проводника.

Возвращаясь к опыту вращения рамки во внешнем магнитном поле, нам следует её вращение рассматривать с позиции изъятия квантов γ + (м) и γ −(м) из этого поля кольцевыми Э.У.к подвижных электронов. При этом будем исходить из того, что изъятие квантов осуществляется только теми участками проволочного контура, которые при вращении рамки подвержены действию магнитного поля − это участки ЛК и СД. Там же, где нет пересечения проводника с линиями индукции внешнего магнитного поля, там и нет перехода квантов на Э.У.к электронов. В нашем примере таковыми участками являются участки проволочного контура ЛС и КД.

Итак, теперь мы исходим из того, что при вращении участков ЛК и СД, находящиеся в них подвижные электроны, своими Э.У.к. пересекают потоки квантов γ + (м) и γ −(м), изымают их из этих потоков и в последующем отправляют во внутрь проводника. При этом попутно заметим, что плоскости Э.У.к подвижных электронов, при вращении рамки располагаются вдоль проводника, т. е. вдоль участков ЛК и СД, а не в перпендикулярно к ним. Это результат взаимодействия подвижных электронов с виртуальными квантами γ + (в) и γ −(в), которые насквозь каналируют участки ЛК и СД.
Только однажды, когда рамка занимает положение параллельное линиям индукции магнитного поля, т. е. когда t = 0, плоскости с Э.У.к. с направлением вектора индукции магнитного поля В составляют угол Φ = 90° . В остальных же случаях они ориентируются к нему под разными углами, от 0 −ля до 90°.
Подобная ориентация плоскостей Э.У.к подвижных электронов вдоль проводника, накладывает определённые трудности в определении площади участка в потоках квантов γ + (м) и γ −(м), с которого "изымаются" эти кванты. Если не учитывать площадь, занимаемую кольцевыми Э.У.к. по обе стороны от участков ЛК и СД, при пересечении ими линий индукции внешнего магнитного поля, то условно можно считать, что площадь этих участков ограничена размерами проводника, где действуют силы Лоренца.
В простом исчислении она равна произведению длины проволочного участка ЛК или на диаметр проволоки. Но так как рамка вращается, то площадь, с которой происходит изъятие квантов γ + (м) и γ −(м) из магнитного потока, будет равна площади, описываемой участком ЛК или СД.
А так как данные участки проволочного контура периодически перемещаются из нижней точки круговой траектории в верхнюю, то площадь, с которой происходит изъятие квантов γ + (м) и γ −(м) из магнитного потока между полюсами постоянного магнита, в пределе будет равна площади рамки контура.

Но так как в промежуточных положениях на круговой траектории рамка пересекает потоки квантов γ + (м) и γ −(м) под разными углами, то при расчётах необходимо учитывать угол, под которым рамка располагается к направлению потоков этих квантов или к направлению вектора магнитной индукции В. Тем самым в расчёт будет браться не вся площадь рамки, а только та её часть, которая в данный момент времени проецируется на вертикальную плоскость, ибо при её повороте, с данной части участки ЛК и СД изъяли соответствующее количество квантов из магнитного потока между полюсами магнита. При расчётах этот момент учитывается синусом угла наклона рамки к вектору В. Но при этом нужно помнить, что сама площадь рамки не взаимодействует с магнитным потоком. Это прерогатива участков ЛК и СД. А площадь рамки берётся в качестве условного эквивалента по отношению количества квантов γ + (м) и γ −(м), изымаемых кольцевыми Э.У.к подвижных электронов, пребывающих в участках ЛК и СД.

Одновременно с этим следует учитывать и угловую скорость вращения рамки. Ведь от того, с какой скоростью участки ЛК и СД, а вернее Э.У.к , "выметают" кванты γ + (м) и γ −(м) из магнитных, взаимно встречных потоков, зависит и количество изымаемых квантов из магнитного поля. Чем большее их количество изымается в единицу времени, тем и сильнее будет сказываться действие Лоренцевых сил на кольцевые Э.У.к подвижных электронов.
То есть, чем за меньшее время участки ЛК и СД (Э.У.к.) будут производить изъятие квантов γ + (м) и γ −(м) с площади, ограниченной размерами рамки, тем большая ЭДС будет возникать в проводниках. В результате мы должны признать, что величина индуцируемой в рамке ЭДС определяется не скоростью изменения магнитного потока, а количеством изымаемых квантов γ + (м) и γ −(м) в единицу времени. Ведь магнитный поток между полюсами постоянного магнита постоянен во времени и его постоянство не зависит от вращения рамки, а вот количество изымаемых квантов переменно и зависит от угловой скорости вращения рамки.

В завершении анализа опыта по вращению рамки в однородном стационарном магнитном поле, уделим несколько внимания правилу Ленца, согласно которого "... индуцированная Э.Д.С. всегда направлена так, чтобы магнитное поле создаваемого ею тока тормозило процесс, вызывающий индукцию". Считается, что в течение первой четверти периода, когда магнитный поток через рамку возрастает, поле индукционного тока должно ослаблять внешнее поле Н, а в течение следующей четверти периода, когда магнитное поле убывает, наоборот, усиливать его. Отсюда ясно, что в моменты прохождения Э.Д.С. через нуль должно происходить изменение её знака".

Анализируя данный опыт с позиции антиподности по отношению двух взаимно встречных потоков γ + (м) и γ −(м), которые по сути и являются материальной основой магнитного потока между полюсами постоянного магнита, было высказано соображение, что изменение знака Э.Д.С. обусловлено не действием магнитного поля индукционного тока. Перемена её знака − это результат пространственной переориентации осей вращения подвижных электронов, движущихся в пространстве вместе с рамкой по круговой траектории.
Но если это так, то возникает вопрос: " Какова конфигурация магнитного поля вокруг участков ЛК и СД и влияет ли оно на внешнее магнитное поле в плане его усиления или ослабления?"
Ответ: Когда по прямолинейному проводнику пропускается электрический ток, то вокруг него возникает магнитное поле, линии индукции которого кольцеобразно замкнуты и располагаются они перпендикулярно проводнику. Подобная их ориентация по отношению к проводнику определяется соответствующей ориентацией осей вращения подвижных электронов в проводнике относительно потоков γ + (эл) и γ −(эл). А как обстоит дело в случае участков ЛК и СД во вращающемся контуре? Ведь под действием Лоренцевых сил подвижные электроны на этих участках движутся совсем иначе, нежели в случае с прямолинейным током.

В процессе анализа, в первом приближении мы пришли к выводу, что движение подвижных электронов в участках ЛК и СД, вращающегося в магнитном поле проволочного контура, в корне отличается от их движения в случае прямолинейного тока. Их оси вращения располагаются не вдоль проводника, а перпендикулярно его оси. А это соответствующим образом отражается и на пространственной конфигурации магнитного поля вокруг этих участков. Ведь под действием Лоренцевых сил электроны движутся вдоль проводника "боком" и при этом их кольцевые Э.У.к., с одной стороны, располагаются в параллельных плоскостях, а с другой − эти условные плоскости все время остаются параллельными оси проводника, т. е. оси прямолинейных участков ЛК и СД, а также плоскости самой рамки.
В результате магнитное поле в районе участков ЛК и СД, обусловленное экваториальной составляющей магнитного поля электронов, становится не кольцеобразным как в случае прямолинейного тока, а "плоским" в пределах всей длины этих участков. Толщина подобного "плоского" или "пластинчатого" магнитного образования будет равна диаметру проволоки, ибо оси всех подвижных электронов в этом случае параллельны между собой и все они, согласованно боком движутся вдоль участков ЛК и СД.
Подобное расположение кольцевых Э.У.к. подвижных электронов, которое возникает под действием виртуальных квантов γ + (в) и γ − (в), приводит к тому, что при вращении рамки Э.У.к. движутся во внешнем магнитном поле не параллельно его силовым линиям, а пересекают их под разними углами − от 0 −ля до 90° и от 90° до 0 −ля. При таком движении кольцевые Э.У.к. не в состоянии повлиять на внешнее магнитное поле − усилить или ослабить его. Ведь усиление или ослабление внешнего магнитного поля будет только в том случае, если встречно или попутно ему будет направлено "стороннее" магнитное поле (магнитное поле индукционного тока), кванты которого будут или нейтрализовать (компенсировать) действие квантов внешнего магнитного поля, или наоборот − усиливать. А это может быть только в случае, когда направление магнитного поля индукционного тока или совпадает с направлением внешнего магнитного поля, или нет. Другими словами: кванты магнитного поля от индукционного тока в пространстве должны двигаться встречно к однотипным квантам внешнего магнитного поля, или под углом к вектору его магнитной индукции В.
В нашем случае они движутся перпендикулярно внешнему магнитному полю. Функциональная же роль кольцевых Э.У.к. при вращении рамки в однородном стационарном магнитном поле, сводится только лишь к изъятию квантов γ + (м) и γ −(м) из внешнего магнитного поля и получению от них соответствующих, реактивных импульсов.

Сказанное выше относилось к участкам ЛК и СД, но контур содержит участки ЛС и КД, а по ним индукционный ток идет в форме прямолинейного тока и Э.У.к. магнитного поля вдоль этих участков перпендикулярны проводникам. Однако следует иметь в виду, что по этим участкам прямолинейные, индукционные токи пространственно идут в противоположных направлениях и, следовательно, магнитные поля от этих токов будут взаимно компенсировать друг друга и их влияние на внешнее магнитное поле ни в коей мере не скажется.
В итоге мы приходим к выводу, что правило Ленца в случае вращения проволочного контура в однородном стационарном магнитном поле не применимо. Этим выводом мы и закончим рассмотрение функциональной схемы вращения проволочного контура в стационарном однородном магнитном поле.

8. Контуры с током и без в магнитном поле.

8. 1. Контур с током в стационарном однородном магнитном поле.

На рис. 3 в (1) изображена функциональная схема прямоугольной рамки с током в стационарном магнитном поле. Она была приведена в качестве наглядного примера, показывающего одинаковость механизма поворота с механизмами поворота магнитной стрелки и соленоида. Схема была приведена в качестве примера в свете принципа Единства и Подобия, без причинного объяснения процессов, происходящих в ней.

В "Элементарном учебнике физики" под ред. акад. Г.С.Ландсберга, т. 2, М., 1966 г. приводятся схемы 251 и 252 (см. стр. 310); в статье рис. 94 и рис. 95, в которых задаётся исходное и конечное положения рамки с током, находящейся в однородном магнитном поле.





Проанализируем события в этих схемах с позиции антиподно − эквивалентной методики. Конечным результатом подобного анализа будет определение направления действия реактивных или Лоренцевых сил в кольцевых Э.У.к. подвижных электронов под воздействием квантов γ + (м) и γ −(м) внешнего магнитного поля.
Для начала определим положение условных плоскостей Э.У.к. подвижных электронов по участкам в контуре относительно силовых линий магнитного поля. С этой целью рассмотрим их положение в двух секущих плоскостях, которые взаимно перпендикулярны и одновременно перпендикулярны плоскости контура (рамки). На рисунке 94а это сечения А − А и Б − Б.




Сечение А − А пересекает участки контура L1 и L2, а Б − Б, участки L3 и L4. В первом ток идёт к наблюдателю, во втором наоборот, от наблюдателя. Соответственно, подвижные электроны в противоположном направлении. Для электронов участка L1 встречный поток квантов γ + (эл) направлен к наблюдателю, а попутный γ −(эл) от него. Первый поток в сечении участка L1 условно изображён в виде красной точки, второй, попутный − в виде синего крестика (см. сечение А − А).
Кванты γ + (эл), после перехода на "свои" кольцевые Э.У.к электронов этого участка, трансформируются в кванты γ + (м) и будут двигаться по ним, согласно правила в п.10 (Правило Левостороннего Буравчика), по часовой стрелке; кванты γ −(эл), соответственно, γ −(м), по "своим" против (с точки зрения стороннего наблюдателя).
Для подвижных электронов участка L2, попутный поток квантов γ + (эл) направлен от наблюдателя, а встречный γ −(эл) к нему. Первый поток в сечении участка L2 условно изображён в виде красного крестика, второй, встречный − в виде синей точки (см. сечение А − А на рис. 94).
Кванты γ + (эл), после перехода на "свои" кольцевые Э.У.к электронов этого участка, трансформируются в кванты γ + (м) и будут двигаться по ним, согласно правила в п.10 (Правило Левостороннего Буравчика), против часовой стрелки; кванты γ −(эл), соответственно, γ −(м), по "своим" по (с точки зрения стороннего наблюдателя).

Теперь учтём, что кванты γ + (м) внешнего магнитного поля "атакуют" участки L1 и L2 в направлении слева − направо, а кванты γ −(м) справа − налево. Следовательно, и Э.У.к. подвижных электронов этих участков, с учётом позонного экранирующего эффекта, будут "атаковываться" квантами γ + (м) слева, а справа квантами γ −(м). Суммарные силы от реактивных импульсов этих квантов образуют момент, который через осредство электронов повернёт контур на 90° против часовой стрелки (см. сечение А − А). То есть мы получили результат, который согласуется с результатом на практике − см. рис. 94б.
На рисунке 94а участки L3 и L4 располагаются параллельно силовым линиям магнитного поля и подвижные электроны этих участков движутся вдоль них. Плоскости кольцевых Э.У.к этих электронов будут перпендикулярны силовым линиям магнитного поля и его квантами будут "атаковываться" без наличия экранирующего эффекта (см. сечение Б − Б на рис. 94). В результате, суммарные реактивные импульсы или силы в системе антиподных Э.У.к подвижных электронов взаимно компенсируются и соответствующий от них суммарный момент станет равным нулю. Тем самым, при положении контура параллельно вектору В магнитного поля, участки L3 и L4 никакого действия со стороны этого поля не будут испытывать.

Совсем другая картина будет "наблюдаться" в отношении участков контура, когда он повернётся на 90° . В этом положении плоскости кольцевых Э.У.к. электронов всех участков, при наличии тока в контуре, будут параллельны силовым линиям магнитного поля (см. сечения В − В и С − С на рис. 95). Все Э.У.к. будут пересекать их и с учётом экранирующего в них эффекта, в них от реактивных импульсов от γ + (м) и γ −(м) возникнут суммарные антиподные реактивные силы, которые в параллельных участках будут взаимно противоположны. По направлению они перпендикулярны участкам контура и располагаются в его плоскости (см. сечения В − В и С − С на рис. 95). При заданном направлении тока (см. рис. 95), контур под действием этих реактивных сил, будет растягиваться в плоскости, перпендикулярной линиям магнитного поля. При обратном направлении тока он будет наоборот, сжиматься.

8.2. Контур с током в неоднородном магнитном поле.

Для начала приведу короткую выдержку из учебника "Курс Общей Физики" авт. И.В.Савельев, т. 2. "Электричество и Магнетизм, Волны. Оптика", м., 1978 г., стр. 128 ÷ 130.

"... Для простоты будем считать контур круговым. Предположим, что поле изменяется быстрее всего в направлении Х, совпадающем с направлением вектора магнитной индукции В, где расположен центр контура и что магнитный момент контура Рм ориентирован по полю (см. рис. 96а и 96б).


При произвольном угле α между векторами Рм и В, вектор магнитной индукции можно разложить на две составляющие: параллельную Вп. и перпендикулярную В⊥ , вектору Рм. Составляющая Вп. обусловливает силы, растягивающие или сжимающие контур (для В = const − см. сечение В − В и С − С на рис. 95). Составляющая В, величина которой равна В sin α , приводит к возникновению вращательного момента (см. сечение А − А, рис.95).
Когда В ≠ const , сила Fдействующая на каждый элемент контура, перпендикулярна к В, т. е. линии магнитного поля в месте пересечения её с элементом контура ΔL. Поэтому силы, приложенные к различным элементам контура, образуют симметричный конический веер (см. рис. 96в). Их результатирующая, сила F, направлена в сторону возрастания В и, следовательно, втягивает контур в область более сильного поля.
Если изменить направление тока на обратное (при этом Рм станет противоположным В), направление результатирующей силы F изменится на обратное. При такой взаимной ориентации векторов Рм и В контур будет выталкиваться из поля (см. рис. 96г).

Вопрос: "Согласуется ли такая (несколько упрощённая) трактовка поведения контура, с его поведением в неоднородном магнитном поле?"

При ответе на этот вопрос воспользуемся антиподно − эквивалентной методикой и прорисуем согласно ей схему действия потоков γ + (м) и γ −(м) неоднородного магнитного поля на контур. Подобную прорисовку сделаем в двух вариантах, соответствующим двум направлениям тока в контуре (см. рис. 97а и 97б).


а) б)
эти буквы расположить под рисунками

На этих условных рисунках показан не только причинный механизм возникновения суммарной силы F, но и направление действия её составляющих Δ F. Результат условной прорисовки полностью совпадает со сведениями, излагаемыми в учебниках по физике для высших учебных заведений (схемы рисунков 96а; б; в и г заимствованы автором из учебника "Курс общей физики" авт. И.В.Савельев, т. 2, М., 1978 г. ; в учебнике это рисунки 46.3 и 46.4).


9. Правило Ленца и электромагнитная индукция.

При изложении вопроса об электромагнитной индукции, не раз делалась ссылка на правило Ленца. По данному правилу определяется направление индукционного тока в индукционном контуре по отношению первичного тока, создающего внешнее магнитное поле.
В вышеприведённых примерах, заимствованных автором из элементарного учебника по физике под редакцией академика Г.С Ландсберга (М., 1966 г.), направление индукционного тока в рассматриваемых схемах индукционного характера, задаётся без анализа истинных причин, приводящих к его возникновению. Знание таковых предопределяет "наполнение" правила Ленца причинным содержанием. Но для этого необходимо, хотя бы в первом приближении, выявить те процессы, под действием которых подвижные е− −ны в индукционном контуре приводятся в движение.
В правиле Ленца ссылки на подобные процессы отсутствуют. В своей основе оно содержит лишь обязательное требование − индукционный ток посредством своего магнитного поля или ослабляет внешнее магнитное поле, когда последнее усиливается, или усиливает его в случае его ослабления. Подобное усиление или ослабление принимается как факт, имеющий место в электрических схемах индукционного характера.
Методика в определении направления индукционного тока, в основе которой лежит правило Ленца, оставляет в стороне непосредственных участников в электромагнитной индукции − подвижные е− −ны, виртуальные кванты γ + (в) и γ −(в), а также магнитные γ + (м) и γ −(м). Ведь от того, как эти кванты взаимодействуют с подвижными электронами в индукционном контуре, зависит не только их ориентация относительно проводника, но и направление, в котором они должны двигаться в нём относительно первичного тока.
К сказанному следует добавить и другое: индукционный ток возникает только в тех участках проволочного контура или проводах, которые подвержены действию "изменяющегося" во времени магнитного потока или потоков квантов γ + (м) и γ −(м). Подвижные е− −ны на этих участках движутся совсем иначе, нежели в остальной части проволочного контура. При обычных условиях, когда отсутствуют силы Лоренца, эти е− −ны, под действием стороннего, внешнего электрического поля прикладываемого к проводнику, движутся вдоль него так, что их оси вращения всё время ориентируются вдоль него или по направлению антиподных потоков квантов γ + (эл) и γ −(эл) в проводнике.
В случае же "изменяющегося" магнитного потока, подвижные е− −ны вдоль проводника движутся "боком". На остальных же участках замкнутого контура, находящихся вне действия антиподных потоков этих квантов, эти е− −ны движутся под действием взаимного проталкивания. Их пространственная ориентация осуществляется за счёт потоков виртуальных квантов.
Подобное их продвижение обусловлено действием Лоренцевых сил на участках разделения зарядов. Они (образно) как бы выталкиваются с этих участков в определённом направлении и это направление, через посредство кольцевых Э.У.к подвижных электронов, задаётся квантами γ + (м) и γ −(м) из внешнего магнитного поля. Попутно заметим, что во внешней части контура отсутствуют электрические кванты γ + (эл) и γ −(эл), ввиду отсутствия внешнего электрического поля.

А теперь, по антиподно − эквивалентной методике определим направление магнитного поля в кольцевом контуре (кольце) и тоже сделаем в однослойном соленоиде (катушке).

По принятому правилу направление тока в проводящем контуре противоположно направлению движения в нём подвижных электронов. Пусть, например, электрический ток в кольцевом контуре К1 (см. рис. 98а) движется по направлению против часовой стрелки. Соответственно, подвижные в нём электроны будут двигаться по часовой стрелке. Их движение происходит под действием двух антиподных потоков квантов γ + (эл) и γ −(эл) − электрического поля, прикладываемого к контуру. На схеме электрон условно изображён в виде небольшого синего кружка, на верхнем и нижнем участках кольцевого контура.


В процессе взаимодействия с этими квантами, подвижные электроны переводят их на свои кольцевые Э.У.к., после чего эти кванты "несут" уже не электрическую, а магнитную функцию. Направление их движения по Э.У.к. мы определим с помощью стороннего наблюдателя по Правилу Левостороннего Буравчика. Наблюдателя расположим слева от контура (см. рис. 98а).

На виде справа ( см. рис. 98б), в верхней части кольцевого участка, электроны будут идти от стороннего наблюдателя, (условно) за чертёж. В соответствии с правилом в п.10 (Правило Левостороннего Буравчика) кванты γ + (эл) − стрелка красного цвета, после того как окажутся на "своих" Э.У.к., должны будут "обходить" их по отношению стороннего наблюдателя по часовой стрелке. Соответственно, кванты γ −(эл) − стрелка синего цвета, "свои" Э.У.к. против часовой − (примечание: на рис. 98б изображены линии магнитной индукции /Э.У.к./ поля кругового тока. Показаны лишь линии, лежащие в одной из плоскостей, проходящей через ось тока. Подобная же картина имеет место в любой из этих плоскостей. В качестве базового рисунка для рисунка 98б, автором задействован рисунок 47.3. из учебника "Курс общей физики" т.2., авт. И.В. Савельев, изд. "Наука", М., 1978 г.).
В нижней части кольцевого контура картина "обхода" этими квантами "своих" Э.У.к.. будет противоположной в виду того, что в этой части контура подвижные электроны движутся к стороннему наблюдателю. Кванты γ + (эл) по отношению стороннего наблюдателя будут по "своим" Э.У.к. двигаться против часовой стрелки, а кванты γ −(эл) по "своим", по часовой.

"Изменение" направления обхода "своих" Э.У.к. квантами в данном случае носит чисто умозрительный характер. Они все время "обходят" свои Э.У.к. в одном направлении. Но при движении по кольцу подвижные электроны совершают оборот в пространстве на 180° по отношению стороннего наблюдателя. Так же на 180° , по отношению стороннего наблюдателя, разворачиваются и плоскости с Э.У.к. И если в верхней части картину "обхода" квантами Э.У.к. условно можно считать "прямой", то в нижней − "перевёрнутой".
Исходя из схемы движения этих квантов по "своим" Э.У.к., "ставшими" γ + (м) и γ −(м), мы вправе утверждать, что на виде справа (рис. 98б), на выходе из кольца с правой стороны, будет располагаться Северный магнитный полюс, а с левой − Южный. Данное их расположение, определяемое по антиподно − эквивалентной методике, полностью согласуется с принятым на сегодняшний момент правилом, определяющим положение магнитных полюсов в соленоидах по направлению электрического тока:



если электрический ток по отношению стороннего наблюдателя обходит виток соленоида (катушки) по часовой стрелке, то с этой стороны соленоида (катушки) располагается Южный магнитный полюс, если против часовой стрелки, то Северный. Подобное расположение полюсов будет и у кольца на схеме 98б (см. рис. 98). При этом особо следует подчеркнуть: магнитное поле прямолинейного тока, тоже и в случае кольцевого − пр. Е и П −ия, образуется за счёт Э.У.к. подвижных электронов, т. е. экваториальной магнитной составляющей магнитного поля электрона. Его меридиональная составляющая ни какого участия в этом деле не "принимает"! . . .

А теперь попробуем причинно установить направление движения подвижных электронов в индукционном контуре, соответственно и индукционного тока без использования правила Ленца.
Рассмотрим следующий пример. На рис. 98а изображён кольцевой контур К1. Ток в этом контуре можно изменять посредством реостата. При увеличении тока J в контуре К1, поток магнитной индукции или плотность антиподных потоков квантов γ + (м) и γ −(м) через контур К2 будет возрастать. Это приведёт к появлению в контуре К2 (см. рис. 98в) индукционного тока Jι, регистрируемого гальванометром (G). При уменьшении тока в контуре К1, будет наблюдаться обратная картина − в контуре К2 появится индукционный ток J? (см. рис. 98г), но уже противоположного направления.

Отметим немаловажные детали, присущие контуру К2:
а) По характеру взаимного расположения Э.У.к. в верхней и нижней частях (в плане рисунка) кольцевого контура К1 на выходе их него, можно утверждать, что индукционный контур К2 пребывает в неоднородном магнитном поле. При этом линии индукции такого поля "атакуют" контур К2 не по направлению нормали к контуру К1, а под соответствующим углом. Это позволяет считать (примерно), что подвижные электроны со стороны внутренней части кольцевого контура К2 "атакуются" потоком квантов γ + (м), а с внешней, потоком квантов γ −(м).
б) Индукционный ток в контуре К2 может возникать при следующих обстоятельствах: при увеличении или уменьшении тока в контуре К1; повороте его так, чтобы изменился угол между нормалью к контуру и направлением поля; поступательное перемещение контура К2 относительно контура К1 или контура К1 относительно контура К2.
в) Так как контур К2 не подключён к внешнему источнику тока, то в нём отсутствуют потоки электрических квантов γ + (эл) и γ −(эл) и при постоянном токе в контуре К1 подвижные электроны в контуре К2 перемещаются хаотично.

Вопрос: "Какое требование следует "предъявить" к подвижным электронам контура К2, чтобы они под действием квантов γ + (м) и γ −(м) контура К1, пришли в движение в направлении, обратном направлению движения подвижных электронов в контуре К1?"

Ответ: Если мы будем исходить их того, что движение подвижных электронов в контуре К2 при возникновении индукционного тока осуществляется под действием Лоренцевых сил, то их движение по проводнику должно быть "боковым" и своими осями вращения они должны "смотреть" в направлении кольца К1 (рис. 98б, д, ж). Тогда, по заключению стороннего наблюдателя, "находящегося" справа от контура К1 (см. рис. 98б, вид по стрелке А), кванты γ + (м) по "своим" Э.У.к в подвижных электронах контура К2, находящихся в верхней части кольца, должны двигаться против часовой стрелки, а кванты γ −(м) по "своим" − по часовой (см. рис. 98в). Такое же направление обхода квантами γ + (м) и γ −(м) будет в Э.У.к. электронов и в нижней части кольцевого контура К2 − кванты γ + (м) против часовой, а γ −(м) по (примечание: направление "обхода" квантами γ + (м) и γ −(м) "своих" Э.У.к. подвижных электронов контура К2 мы определяем с помощью виртуальных квантов γ + (в) и γ −(в)).
Но это произойдёт только в том случае, если кольцевые Э.У.к. подвижных электронов контура К2 будут пересекать линии индукции магнитного поля от тока J контура К1 или потоки квантов γ + (м) и γ −(м).


Подобное пересечение будет возможно в двух случаях. В одном случае, кольцо К2 относительно кольца К1 неподвижно, а происходит перемещение линий индукции магнитного поля тока J контура К1 относительно кольца К2. В другом, кольцо К2 перемещается относительно контура К1, т. е. оно или приближается к нему, или удаляется от него − подобное движение контура К2 идентично движению электрона в магнитном поле прямолинейного тока, когда он движется в направлении к проводнику, или от него (см. рис. 103 в этой статье).

В обоих этих вариантах подвижные электроны контура К2 будут двигаться в магнитном поле от тока J контура К1. При этом должна соблюдаться пространственная ориентация подвижных электронов контура К2 по отношению направления их движения в пространстве. А так как кольцо К2, а следовательно, и подвижные в нём электроны или приближаются к кольцу К1, или удаляются от него, то правомерен следующий вопрос: "Под действием потоков каких квантов подвижные электроны контура К2 сориентируются подобающим образом?"

Исходя из рассмотренных выше примеров, пока будем исходить из того, что в "обязанность" квантов γ + (м) и γ −(м) из магнитного поля от тока J контура К1 подобная функция не входит. Во всех разобранных выше примерах этой функцией наделялись виртуальные кванты γ + (в) и γ −(в), которые воздействуют на меридиональную составляющую магнитного поля электрона по направлению его движения в пространстве, или по направлению вектора его скорости. И только после того, как эти кванты "зададут" надлежащую пространственную ориентацию подвижным электронам контура К2, только после этого в "работу" вступают и кванты внешнего магнитного поля отпрямолинейного тока контура К1, которые и "обеспечивают" наличие Лоренцевых сил в кольцевых Э.У.к. подвижных электронов контура К2 (примечание: следует иметь в виду, что своё действие на подвижные электроны кванты обоих видов оказывают одновременно).

Исходя из этих соображений, при движении контура К2 в направлении контура К1, подвижные электроны контура К2 должны "смотреть" в направлении контура К1 своим Северным магнитным полюсом, а в обратном − Южным ( см. рис. 98д). При удалении же контура К2 от контура К1 (см. рис. 98ж) направленность действия квантов γ + (в) и γ &minus (в) на подвижные электроны контура К2 будет противоположной.
Теперь, в направлении контура К1 электроны контура К2 будут "смотреть" своим Южным магнитным полюсом, а от него − Северным. Те есть изменение направления движения контура К2 на противоположное, сразу же отражается на пространственной ориентации подвижных электронов. Они оборачиваются в пространстве проводника на 180° . При этом следует отметить, что оборачиваемость электронов происходит от действия квантов γ + (в) и γ −(в) на их меридиональные Л.П.м. /в качестве примера см. рис.1 в (1)/.
Подобная пространственная оборачиваемость отразится и на пространственном положении плоскостей Э.У.к. подвижных электронов контура К2. Они тоже развернутся на 180° , а в результате изменится и направление Лоренцевых сил. Они на кольцевые Э.У.к. подвижных электронов контура К2 будут действовать в противоположном направлении (см. рис. 98г). И как следствие этого, гальванометр отметит в цепи появление противоположно направленного индукционного тока.

Из практики проведения данного опыта известно, что при движении конура К2 в направлении контура К1 или наоборот, в первом случае возникает сила отталкивания, а во втором, сила притяжения контуров. Считается, что при сближении кольцевых контуров, на сторонах колец, обращённых друг к другу, возникают одноимённые магнитные полюса (см. рис.98д), а при удалении − разноимённые (см. рис. 98ж).

В данном случае уместен следующий вопрос: "Какие Л.П. подвижных электронов в контуре К2 участвуют в деле возникновения магнитных полюсов, а какие в деле возникновения сил сопротивления?".
Ответ на данный вопрос носит предположительный характер и логически он "исходит" из предназначенности экваториальных (Э.У.к.) и меридиональных Л.П.м. электронов.

Действительно, ведь в возникновении индукционного тока принимают одновременное участие обе структуры электрона. Экваториальные Э.У.к. участвуют в деле их продвижения по кольцу, а меридиональные Л.П.м. − в надлежащей их пространственной ориентации. Первые располагаются в плоскостях, параллельных плоскости контура К2 и, следовательно, контуру К1; вторые в плоскостях, перпендикулярных и К1, и К2. Получается, что эти, т. е. меридиональные Л.П.м., участвуют в образовании магнитных полюсов у контура К2 во время его движения относительно контура К1 и одновременно, в возникновении сил отталкивания или притяжения между контурами (см. рис. 98д и 98ж).
Когда контур К2 движется к контуру К1, подвижные в нём электроны в направлении кольца К1, под действием квантов γ + (в) и γ − (в), ориентируются Северными магнитными полюсами. Такая их ориентация приводит к тому, что выход меридиональных Л.П.м. южного направления из подвижных электронов ориентирован в направлении от кольца К1, а северных Л.П.м. − в направлении к кольцу К1. В результате и получается, что при сближении контуров К1 и К2 они обращены друг к другу одноимёнными, Южными магнитными полюсами (см. рис. 98д). При удалении контуров друг от друга, всё будет наоборот − разноимёнными магнитными полюсами. Южный у кольца К1 останется на месте, а у кольца К2 Южный поменяется на Северный и, соответственно, Северный на Южный.
Если мы поменяем направление тока в контуре К1, то картина расположения магнитных полюсов должна измениться. В случае сближения, они будут обращены друг к другу Северными магнитными полюсами. При удалении, у контура К2, со стороны контура К1, будет располагаться Южный магнитный полюс, а в направлении к нему, у контура К1 − Северный.

Сближение и отодвигание контуров К1 и К2 одновременно предопределяет и движение под действием Лоренцевых сил подвижных электронов в контуре К2. При этом своими меридиональными Л.П.м. они пересекают кольцевые Э.У.к. подвижных электронов контура К1 или линии магнитной индукции прямолинейного тока. Это приводит к возникновению Лоренцевых сил в меридиональных Л.П.м. контура К2 в направлении контура К1 или от него. При этом следует иметь в виду, что эти силы также являют собой реактивные силы, которые возникают в Л.П.м. в следствие "перехода" квантов γ + (м) и γ −(м) с Э.У.к. или линий индукции от магнитного поля контура К1 на Л.П.м подвижных электронов контура К2.
Но с данным процессом одновременно идёт и обратный процесс − "переход" квантов γ + (м) и γ −(м) с Л.П.м. подвижных электронов контура К2 на линии индукции магнитного поля контура К1. Это приводит к возникновению магнитных сил отталкивания и притяжения − (на рис. 98ж и д эти силы у кольца К2 обозначены как Fлор., а у кольца К1 как Fм).
О процессе подобного "перехода" или "перескакивания" мы уже говорили, когда разбирали функциональную схему взаимодействия параллельных проводников, по которым пропускается ток или в одном, или в противоположном направлении, а также при разборе схем взаимодействия полосовых постоянных магнитов.

Так как меридиональные Л.П.м. подвижных электронов контура К2, в процессе их движения по контуру располагаются (условно) в плоскостях, перпендикулярных плоскости кольца К1 и К2, и тоже можно сказать и о линиях индукции магнитного поля контура К1, то это приводит к тому, что реактивные силы Fлор. в Л.П.м. подвижных электронов контура К2 и F(м) в линиях индукции контура К1, будут действовать в направлении плоскостей обоих колец (кольцевых контуров). При встречном движении колец эти силы будут препятствовать их сближению, а при удалении наоборот, препятствовать их удалению.
В случае рисунка 98д, отталкивание колец будет происходить при условии, что кванты γ + (м) взаимно обратно "переходят" с Э.У.к. контура К1 на Л.П.м. подвижных электронов контура К2 и наоборот. Но одновременно, эти же кванты также участвуют и в процессе возникновения Лоренцевых сил в Э.У.к подвижных электронов контура К2, что приводит к "боковому" их перемещению по этому контуру. При этом следует иметь в виду, что их взаимообратный "переход" осуществляется преимущественно внутри контуров, где имеется более высокая плотность линий магнитной индукции, нежели снаружи их.

В противоположность квантам γ + (м), кванты γ −(м) (для случая 98д.) воздействуют на подвижные электроны контура К2 внешним образом и их движение по Л.П.м. подвижных электронов контура К2 преимущественно направлено в сторону от кольца К1. Соответственно реактивные силы от них, наоборот, направлены в направлении кольца К1.
В первом приближении можно считать, что для случая рисунка 98д, отталкивание контуров в основном происходит за счёт реактивных сил, возникающих в процессе взаимно обратного перехода квантов γ + (м) внутри обоих контуров на соответствующие Л.П. В случае рисунка 98ж, притяжение контуров в основном "обеспечивается" тоже во внутренней их части соответствующим "переходом" как квантов γ + (м) с линий магнитной индукции от контура К1 на Л.П.м. подвижных электронов контура К2, так и квантов γ −(м) с этих, но антиподных Л.П.м., на "свои" Э.У.к. в магнитное поле контура К1. Возникающие при таком "переходе" реактивные силы будут притягивать оба контура и препятствовать их удалению. В этом случае, так же как и в случае рисунка 98д, оба вида этих квантов принимают одновременное участие и в "боковом" продвижении подвижных электронов по контуру К2.
Если предполагать, что плотность взаимного расположения меридиональных Л.П.м. внутри контура К2 больше, нежели снаружи, то в силовом отношении суммарные Лоренцевы силы, возникающие внутри него в южных Л.П.м., будут больше, нежели в северных Л.П.м снаружи. При выполнении этого условия, сближающиеся контуры К1 и К2 будут отталкиваться друг от друга, а при удалении наоборот − притягиваться (см. рис. 98д и 98ж) *).

*) Информация к размышлению по отношению рис. 98.

Из практики известно, что когда к соленоиду приближается полосовой постоянный магнит своим Северным магнитным полюсом, то на конце соленоида, обращённого к приближающемуся магниту, возникает одноимённый, Северный магнитный полюс, при удалении Южный. Эта особенность учитывалась автором при прорисовке функциональных схем отталкивания и притяжения контуров К1 и К2 (см. рис. 98д и ж).
В случае рисунка 98д, ориентация подвижных электронов контура К2 в момент его приближения к контуру К1, определялась посредством виртуальных квантов γ + (в) и γ −(в). Так как подвижные электроны вместе с контуром К2 в направлении контура К1 движутся слева − направо (см. рис. 98д), то встречным для них потоком виртуальных квантов должен быть поток γ + (в), направленным в сторону от контура К1 (т. е. справа − налево в плане рисунка) и сами электроны в направлении контура К1 должны "смотреть" своим Северным магнитным полюсом.
Такая ориентация подвижных электронов контура К2 и приводила к тому, что на выходе справа (в плане рисунка) у контура К2, за счёт южных их меридиональных Л.П.м. располагался Южный магнитный полюс и в момент сближения оба контура были обращены друг к одноименными, Южными магнитными полюсами. Такое совместное расположение полюсов обеспечивалось соответствующей направленностью "южных" меридиональных Л.П.м. подвижных электронов контура К2 и "южных" Э.У.к. подвижных электронов контура К1. А наличие обменного процесса между ними квантами γ + (м) и обеспечивало наличие реактивных сил, действие которых в момент сближения контуров и приводило к их взаимному отталкиванию.

В случае рисунка 98ж − отодвигание контура К2 от контура К1, направленность подобных процессов должна быть противоположной, ибо направление действия виртуальных квантов γ + (в) и γ −(в) на подвижные электроны контура К2 становится противоположным, нежели на рисунке 98д. Здесь также меняется и направление "обхода" квантов γ + (м) и γ −(м) по меридиональным Л.П.м. у подвижных электронов контура К2. Если на схеме 98д кванты γ + (м) условно "шли" в направлении контура К1, то на схеме 98ж от него. То же произошло с квантами γ −(м).

Но к этим изменениям добавилось и другое. Если в схеме 98д отталкивание контуров происходило за счёт обменного процесса квантами γ + (м) преимущественно внутри контуров, то в схеме 98ж притяжение контуров в основном осуществляется за счёт обоих квантов и γ + (м), и γ −(м). Первые "переходят" с Э.У.к. подвижных электроновконтура К1 на "южные" Л.П.м. подвижных электронов контура К2, а γ −(м) с "северных" Л.П.м. подвижных электронов контура К2 на "свои" Э.У.к. подвижных электронов контура К1.
Процесс притяжения, осуществляемый за счёт квантов обоих видов, преимущественно, как и в схеме 98д, идет во внутренней области обоих контуров. Подобную картину мы уже рассматривали в случае взаимодействия разноимённых магнитных полюсов плоских постоянных магнитов − см. рис. 41.

Кроме рисунка 98 в статье приводится и рисунок 99. В нём, в отличии от рис.98, контур К2 при движении в направлении контура К1 движется навстречу Северного его магнитного полюса. Все события до схем 99д и ж идентичны подобным событиям в рисунке 98, только с противоположной направленностью. А вот схемы 99д и ж имеют принципиальное методическое отличие от подобных 98ж и д. Данное различие обусловлено применяемой антиподно − эквивалентной методикой в определении ориентации подвижных электронов контура К2 при его движении к контуру К1 или при его удалении.
В случае рис.98, ориентации подвижных электронов определялась с помощью виртуальных квантов γ + (в) и γ −(в). С помощью её выявлялась требуемая ориентация подвижных электронов контура К2 по отношению контура К1 с тем, чтобы на выходе их меридиональных Л.П.м. в направлении контура К1, у контура К2 был Южный магнитный полюс в момент сближения контуров. Северный же магнитный полюс, в момент расхождения. В случае рис. 98 данная методика полностью себя оправдала, чего не скажешь в отношении рис. 99д и ж.

Действительно, при приближении контура К2 к контуру К1, согласно данной методики, встречным потоком для подвижных электронов контура К2 должен быть поток γ + (в) направленный в направлении от контура К1. В результате, подвижные электроны контура К2 должны в направлении контура К1 сориентироваться своим Северным магнитным полюсом. Это привело бы к тому, что контур К2 в направлении контура К1 ориентировался бы своим Южным магнитным полюсом. И вместо того, чтобы контуры отталкивались, они бы наоборот, при сближении притягивались. Однако из опыта мы знаем, что они наоборот, отталкиваются.
То же имеет место и в случае рис. 99ж. При использовании данной методики контур К2 "смотрел" на контур К1 не Южным, а своим бы Северным магнитным полюсом. То есть, в случае рис. 99д, нежели отталкиваться, они притягивались, а в случае рис. 99ж, отталкивались. Но практика показывает обратное.



Напрашивается вопрос: "Как следует поступать, чтобы данная функциональная cхема этого опыта, правильно отражала бы его практическую сторону?"

Ответ: В данном случае, для схем 99д и ж нужно отказаться от методики виртуальных квантов и поступать следующим образом: считать, что при движении контура К2 в сторону Северного магнитного полюса контура К1, подвижные электроны контура К2 в направлении контура К1 ориентируются Южными своими магнитными полюсами. Тогда на выходе у контура К2, в направлении контура К1, образуется Северный магнитный полюс (см. рис. 99д), а в случае схемы 99ж, Южный.

В первом и во втором случаях, магнитные полюса образуются за счёт меридиональных Л.П.м. подвижных электронов контура К2. При таком подходе к функциональным схемам данного варианта этого опыта, они правильно отражают его итоговый конечный результат.
Объяснить же подобную особенность данных функциональных схем 98ж и д и 99д и ж, пока что не представляется возможным. Остановимся пока на том, что когда электроны контура К2 к контуру К1 приближаются своими северными магнитными полюсами, "действует" антиподно − эквивалентная методика виртуальных квантов, а когда своими южными магнитными полюсами, то вместо вертуальных квантов γ + (в) и γ − (в) надо пользоваться квантами γ + (м) и γ −(м).
_____________________________

Подведём итог по данному опыту:

1. Анализ данного опыта был произведён без учёта магнитного потока и изменения его плотности во времени. В качестве главенствующего фактора был выбран фактор Лоренцевых сил. При этом автор исходил из соображения, что индукционный ток представляет собой направленное движение всё тех же подвижных электронов. Но их движение по проводнику возможно под действием только двух факторов: первый − это их движение под действием двух взаимно встречных потоков квантов γ + (эл) и γ −(эл); второй − их движение под действием Лоренцевых сил или квантов γ + (м) и γ −(м).
В контуре К2 первый фактор отсутствовал и движение подвижных электронов, при смещении контура К2 относительно контура К1, могло осуществиться только при наличии второго фактора, т. е. Лорецевых сил. Но для этого, подвижные электроны (образно) должны были "выполнить" определённые "требования". Во−первых, определённым образом сориентироваться в пространстве относительно линий индукции прямолинейного тока контура К1. Во−вторых, своими кольцевыми Э.У.к. пересекать эти линии. "Выполнение" этих требований и определило "сценарий" возникновения индукционного тока в контуре К2 без привлечения к этому переменного во времени обезличенного магнитного потока от тока в контуре К1.

2. В качестве ориентирующих потоков для подвижных электронов контура К2, как и в предыдущих примерах, были использованы потоки виртуальных квантов γ + (в) и γ −(в). Вопрос: "Правомерно ли функцию по ориентации электронов, как бы возлагать на эти кванты?".

Ответ: При ответе будем исходить из установки, что функция по переориентации подвижных электронов кольца К2 есть прерогатива квантов γ + (м) и γ −(м) тока, циркулирующего в контуре К1, а вернее по линиям индукции прямолинейного тока этого контура. Но когда подвижные электроны контура К2, в процессе перемещения попадут под действие квантов γ + (м) и γ −(м), они своими осями сориентируются по направлению касательных к линиям магнитной индукции тока кольца К1 или Э.У.к. Причина такой ориентации обусловлена возникновением момента в меридиональных Л.П.м. подвижных электронов контура К2 (см. напр. условный рис. 1б и 2б в (1)). При этом плоскости экваториальных Э.У.к. подвижных электронов контура К2 должны ориентироваться перпендикулярно к Э.У.к. кольца К1 (примечание: подобные Э.У.к. на условных рисунках 1б и 2б в (1) не показаны). Одновременно они будут перпендикулярны потокам атакующих квантов γ + (м) и γ −(м), циркулирующих в Э.У.к. электронов контура К1. Подобная ситуация показана на условном рисунке 8 в (1).
В этом положении, Э.У.к подвижных электронов контура К2 атакуются квантами γ + (м) и γ −(м) из Э.У.к. контура К1 по всей их длине, что "исключает" возникновение в них Лоренцевых сил и, соответственно, продвижение электронов по контуру К2 /в качестве примера см. рис. 8 в (1/)/. Но практика показывает наличие индукционного тока в контуре К2 при его приближении к контуру К1 или удалении от него.
Подобный ход рассуждений о механизме ориентации подвижных электронов контура К2 и приводит к мысли, что в этом деле должны быть третьи участники. В качестве таковых, исходя из опытов Г.Роуланда и А.А.Эйхенвальда и были задействованы виртуальные кванты γ + (в) и γ −(в). При этом хочется отметить, что ожидаемый итоговый результат в опытах 98 и 99, где задействованы эти кванты, полностью совпадает с итоговым результатом, предусматривающим использование правила Ленца.

От рассмотренного только что варианта возникновения индукционного тока, перейдём к случаю, когда этот ток возникает в результате изменения магнитного потока. В этом случае оба контура относительно друг друга остаются неподвижными. Индукционный же ток в контуре К2 обусловлен изменением тока в контуре К1. Естественно спросить: "А по какому сценарию происходит действие тока контура К1 на подвижные электроны контура К2?"

Ответ: Если исходить из принципа Единства и Подобия, то по своей сути или механизму, этот вариант должен быть подобен только что рассмотренному. То есть изменение магнитного потока предопределяет движение кольцевых Э.У.к. контура К1 в направлении контура К2 или от него.
Исходя из этих соображений (для схемы рисунка 98), в случае возрастания плотности магнитного потока магнитного поля от тока в контуре К1 или потоков антиподных квантов γ + (м) и γ − (м), мы должны сказать, что по отношению контура К2 возникает направленное движение виртуальных квантов γ + (в) и γ −(в). Эти кванты, проходя насквозь контур К2, попутно разворачивают в нём подвижные электроны Северным полюсом в сторону контура К1, а при убывании плотности магнитного потока наоборот, Южным полюсом.
При возрастании магнитного поля, встречным потоком для электронов проводимости контура К2 в направлении от контура К1 к контуру К2 должен быть поток виртуальных квантов γ + (в), а попутным поток γ −(в). Только при этих условиях подвижные электроны контура К2 обернуться Северным магнитным полюсом в сторону контура К1. При выполнении этого условия, поток квантов γ + (в) должен двигаться от контура К1 в сторону контура К2, а поток квантов γ −(в) в обратом направлении. При убывании магнитного поля, направленность движения потоков виртуальных квантов должна быть обратной. Кванты γ + (в) должны двигаться со стороны контура К2 в направлении контура К1, а кванты γ −(в) наоборот − от контура К1 в направлении контура К2.

Изменение направления в развитии плотности магнитного потока с роста на убывание, сразу отражается и на направлении движения виртуальных потоков. Их направление меняется на 180° , а в результате на 180° оборачиваются и подвижные электроны в контуре К2. Они к контуру К1 поворачиваются своим Южным полюсом. Подобная оборачиваемость подвижных электронов контура К2 по отношению контура К1 сказывается на пространственной ориентации их кольцевых Э.У.к. Они по отношению контура К1 разворачиваются на 180° . В результате на 180° в них меняется направление движения квантов γ + (м) и γ −(м) по отношению контура К1 по "своим" Э.У.к. в подвижных электронах и как следствие, меняется пространственное направление реактивных импульсов в системе кольцевых Э.У.к. подвижных электронов контура К2. Хотя данные кванты по этим Э.У.к. будут двигаться в прежнем направлении, но по отношению контура К1 оно обернётся на 180° .
Теперь эти реактивные импульсы или Лоренцевы силы, через посредство Э.У.к., будут "двигать" подвижные электроны по контуру К2 в обратном направлении, а в результате и в обратном направлении будет идти индукционный ток при убывании магнитного поля. Его направление будет совпадать с направлением первичного тока в контуре К1.
В отношении схемы рисунка 99 есть (пока что) неопределённая трудность, которая, как было показано в отношении схем рисунков 99д и ж, обусловлена отказом использования виртуальных квантов γ + (в) и γ −(в) в задании ими определённой пространственной ориентации подвижных электронов контура К2.
Кроме рассмотренных вариантов возникновения индукционного тока в контуре К2, подобное может быть получено за счёт его поворота относительно контура К1 так, чтобы изменился угол между нормалью к контуру и направлением поля. Этот вариант идентичен случаю поворота прямоугольной рамки в магнитном поле, который был рассмотрен выше.


P.S. В данной статье, так же как и в предыдущей (1), речь в основном шла об антиподно − эквивалентной методике объяснения различных опытов по электромагнетизму с причинных позиций. Данная методика позволяют причинно подойти к объяснению и других электромагнитных явлений. Предлагается Читателю выполнить эту работу самостоятельно.
Автор же перейдёт к вопросу структурно − функционального анализа антиподно − эквивалентного, математического ряда ЭМРN и ряда ЭМР(− ∞ ÷ ∞), и в первом приближении, выскажется по смысловому содержанию информации, которая закодирована не только в пиктограмме квадрат, находящийся в Перу, 14 ° южной широты, но и в пирамидах на плото Гиза в Египте. И как было уже сказано − это будет темой последующей статьи, которую автор постарается разместить в Интерете.


7. 05. 2012. Лавров М.А.






















Оценка: 8.00*5  Ваша оценка:
Связаться с программистом сайта.

Новые книги авторов СИ, вышедшие из печати:
О.Болдырева "Крадуш. Чужие души" М.Николаев "Вторжение на Землю"

Как попасть в этoт список

Кожевенное мастерство | Сайт "Художники" | Доска об'явлений "Книги"