Мак Петр Анатольевич. Вг

Л N4. ТЕМА N 2: ОПРЕДЕЛЕНИЕ КООРДИНАТ ГЕОДЕЗИЧЕСКИХ ПУНКТОВ

1. Понятие о взаимных нормальных сечениях и геодезической линии

На поверхности эллипсоида имеем две точки: точку А с широтой В_А и точку С с широтой В_С причем B_С > В_А , т. е. точка С расположена севернее точки А (рис. 1.1). Докажем, что нормаль АN_A в точке А и нормаль CN_C в точке С пересекают малую ось в различных точках.

0x01 graphic

Рис. 1.1

В плоскости меридиана точки А отрезок ОА₁ от центра эллипса до основания перпендикуляра АА₁, опущенного из точки А на малую ось, согласно (9.8: 0x01 graphic

)), равен

0x01 graphic

В прямоугольном треугольнике N_AAA₁, в соответствии с (10.5: 0x01 graphic

) имеем

0x01 graphic
.

Отрезок ON_A , т. е. расстояние от центра меридианного эллипса до точки пересечения нормали в точке А с малой осью эллипса, будет равен

0x01 graphic

Сделав аналогичный вывод для отрезка ON_C (в плоскости меридиана точки С), получим:

0x01 graphic

Так как B_С > В_А, то ON_C не равно ON_A и ON_С > ON_А . Что и требовалось доказать.

Теперь можно сделать следующие выводы:

1) нормали в различных точках на поверхности эллипсоида, не лежащих на одной и той же параллели, пересекают малую ось эллипсоида в различных точках, при этом чем севернее расположена точка, тем далее от центра эллипса будет это пересечение;

2) плоскость, проходящая через нормаль в точке А и через точку С, не совпадает с плоскостью, проходящей через нормаль в точке С и точку А. Первая плоскость пересекает поверхность эллипсоида по нормальному сечению АаС, а вторая по нормальному сечению СсА. Следовательно, между двумя точками на поверхности эллипсоида проходят два нормальных сечения, называемые взаимными нормальными сечениями. При этом сечение АаС называется прямым нормальным сечением в точке А, а сечение АсС -- обратным нормальным сечением в точке А.

Соответственно в точке С имеем: СсА -- прямое и СаА -- обратное нормальные сечения.

Если начальная точка линии находится (на рис. 1.1 точка А) южнее конечной, то прямое нормальное сечение в ней располагается южнее обратного.

По определению прямого нормального сечения видно, что для получения его между двумя точками на земной поверхности нужно установить теодолит в начальной точке и, приведя его ось вращения в совпадение с нормалью, сделать визирование на конечную точку. Вехи, установленные в полученной визирной плоскости, обозначают прямое нормальное сечение.

Таким образом, наблюдения на каждом триангуляционном пункте делают по направлениям прямых нормальных сечений. Поэтому на каждой стороне треугольников триангуляции прямое и обратное наблюдения делают по различным на местности направлениям, угол между которыми равен углу между взаимными нормальными сечениями. Этот угол, обозначаемый через ?, может быть вычислен по формуле

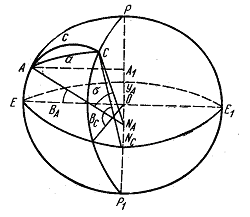
0x01 graphic
,

в которой ? -- угол, образуемый нормалью в начальной точке линии и прямой между точкой пересечения этой нормали с малой осью эллипсоида и конечной точкой линии;

А -- азимут прямого нормального сечения в начальной точке;

В -- широта начальной точки линии.

Величина угла ? малая и зависит от длины линии. Так, при расстоянии между конечными точками линии в 20 км ? = 0",002, при расстоянии 30 км ? = 0",004. Поэтому при длинах сторон до 30 км, а практически в триангуляции 2 класса и ниже, с двойственностью нормальных сечений не считаются и принимают оба взаимные нормальные сечения сливающимися и представляющими одну кривую линию.

В триангуляции 1 класса, где пренебрегать двойственностью нормальных сечений нельзя, в измеренные направления вводят поправки, в результате чего от прямых нормальных сечений пере- ходят к геодезическим линиям.

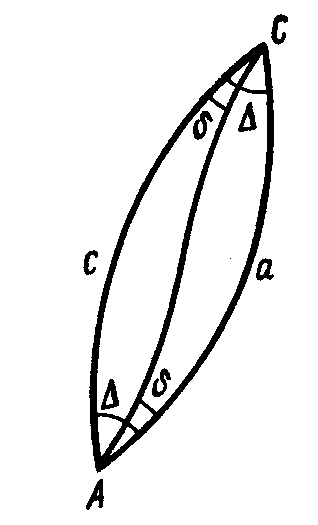
0x01 graphic

Рис. 1.2

Геодезическая линия -- это кривая, являющаяся кратчайшим расстоянием между двумя точками на поверхности эллипсоида. Расположение ее относительно взаимных нормальных сечений схематически показано на рис. 1.2. 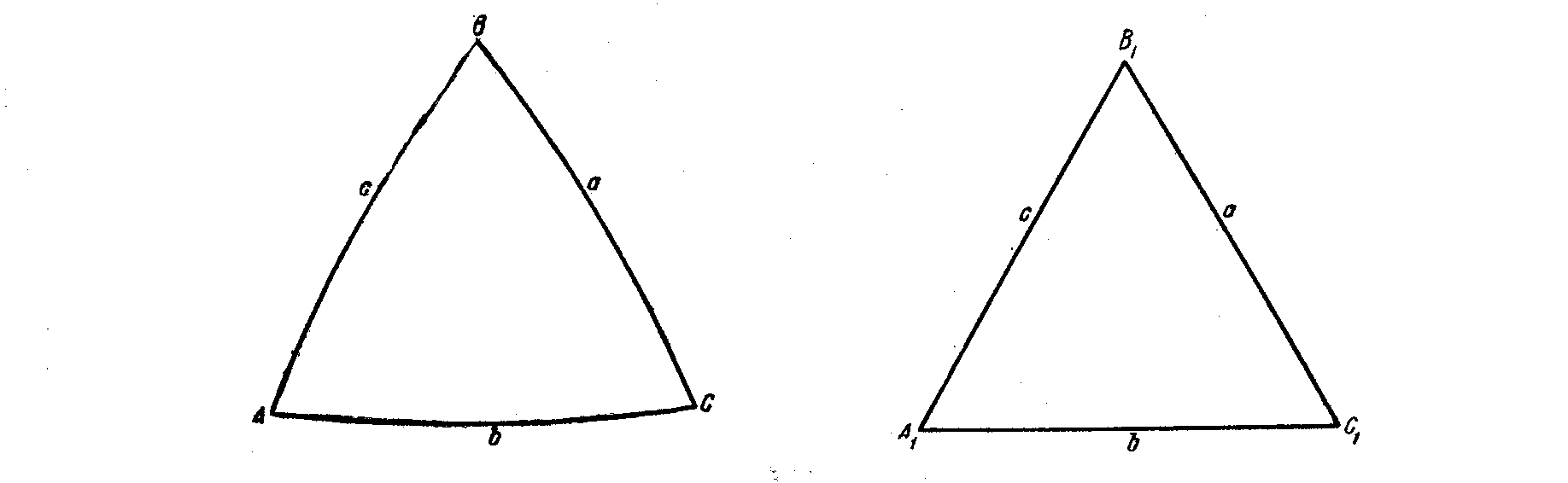Геодезическая линия у своих конечных точек А и С располагается ближе к прямым нормальным сечениям АаС и АсС в этих точках и составляет в них с этими нормальными сечениями угол, приблизительно равный 0x01 graphic

2. Решение малых сферических и сфероидических треугольников

Для начала рассмотрим общие сведения.

После того, как получены окончательные значения измеренных направлений или углов на поверхности эллипсоида, переходят к решению треугольников. Задача заключается в последовательном вычислении длин сторон треугольников триангуляции, причем известными являются одна сторона и углы в каждом треугольнике.

Строго говоря, треугольники триангуляции являются сфероидическими или эллипсоидальными треугольниками, поскольку они образованы на поверхности эллипсоида. На практике обычно приходится иметь дело с треугольниками, стороны которых не превышают 40 -- 50 км и в редких случаях достигают до 70 -- 80 км. Вследствие малой величины сжатия земного эллипсоида различие в элементах сфероидических и сферических треугольников триангуляции (соответственно подобранного радиуса) является малым и, как увидим далее, практически пренебрегаемым. Таким образом, вычисление треугольников триангуляции сводится к решению сферических треугольников. Если решать треугольники по обычным формулам сферической тригонометрии, то стороны необходимо выражать в частях радиуса; но это неудобно, так как в практических целях стороны необходимо иметь в метрах. Поэтому решение треугольников триангуляции выполняют особыми методами, пользуясь так называемой теоремой Лежандра или по способу аддитаментов.

2.1. Решение сферических треугольников по теореме Лежандра

Пояс земного эллипсоида шириной в 200 км (приблизительно 2® по широте) можно принимать за шаровой пояс с радиусом, равным среднему радиусу кривизны R для средней параллели пояса. Стороны треугольников триангуляции редко бывают больше 60 км, а в большинстве случаев они значительно короче, поэтому эллипсоидальные треугольники триангуляции можно считать сферическими с углами, равными измеренным на местности, и решать эти треугольники по формулам сферической тригонометрии. Однако эту задачу можно еще упростить и решать треугольники как плоские, применив теорему Лежандра.

Пусть АВС (рис. 2.1) -- сферический треугольник, стороны которого в линейных единицах обозначим через а b, c. По сторонам а, b, c построим плоский треугольник А₁В₁С₁ (рис. 2.2); углы сферического треугольника обозначим, соответственно через А, В, С, а углы плоского -- через А₁,В₁, С₁.

0x01 graphic

Рис. 2.1 Рис. 2.2

Поставим задачу найти разности углов А -- А₁ , В -- В₁ , С -- С₁. Зная эти разности, мы сможем от сферических треугольников переходить к плоским, имеющим те же значения длин сторон и, таким образом, производить решение треугольников, применяя формулы прямолинейной тригонометрии:

Обозначим через R радиус шара, на котором построен сферический треугольник. Тогда, применяя формулу косинуса стороны для сферического треугольника АВС, напишем:

0x01 graphic
, (2.1)

Как известно из сферической тригонометрии, сумма углов в сферическом треугольнике больше 180® на величину, называемую "сферический избыток" и обозначаемую через ?.

Итак, мы имеем сферический треугольник АВС с углами А, В и С и сторонами а, b и c на шаре радиусом R. Сферический избыток этого треугольника определяется формулой

0x01 graphic
(2.2)

где Р -- площадь плоского треугольника А₁В₁С₁, имеющего такие же стороны, как сферический треугольник АВС.

По теореме Лежандра малый сферический треугольник можно решать как плоский, стороны которого соответственно равны сторонам сферического треугольника, а углы равны углам сферического треугольника, уменьшенным каждый на 1/3 сферического избытка этого треугольника. Следовательно, применяя теорему Лежандра, имеем:

0x01 graphic

Площадь треугольника, входящую в формулу (2.2), принято вычислять по известной формуле

0x01 graphic
,

тогда для вычисления сферического избытка будем иметь формулу

0x01 graphic

По этой формуле сферический избыток вычисляют при длинах сторон треугольника больше 90 км. При сторонах короче 90 км можно ограничиться одним первым ее членом и, кроме того, вместо плоского угла А₁ взять измеренный угол А. Тогда получим для вычисления сферического избытка формулу, которой обыкновенно и пользуются при вычислениях в триангуляции

0x01 graphic
.

Обозначая, как принято, величину, через 0x01 graphic

через f, формулу для ?'' перепишем в окончательном виде

0x01 graphic
. (2.3)

Величина f приводится в таблицах по аргументу широты. Сферические избытки треугольников вычисляют одновременно с предварительным решением треугольников при вычислении поправок направлений за центрировку и редукцию.

При логарифмическом вычислении сферического избытка величина 0x01 graphic

выбирается из специальной таблички, которая приведена в "Таблицах для вычисления геодезических координат. С этим обозначением формула для вычисления сферического избытка примет вид как в (2.2).

При решении треугольников триангуляции II класса и ниже необходимость учета поправочных членов как в теореме Лежандра, так и при вычислении отпадает.

Для общей ориентировки рассмотрим числовые значения сферических избытков при различных длинах сторон (для равносторонних треугольников):

при длине сторон в 5 км ? - 0,07,

10 ? - 0,25,

20 ? - 1,0,

30 ? - 2,0,

60 ? - 8,0.

Вычисление сферического избытка треугольников производится при помощи четырехзначных или пятизначных таблиц логарифмов, обычно одновременно с предварительным решением треугольников.

В табл. 2.1 (прим1_Л4) приводится пример решения малого сферического треугольника по теореме Лежандра.

2.2. Решение треугольников по способу аддитаментов.

Сохраняя прежние обозначения для сферического треугольника ABC имеем:

0x01 graphic
.

Раскладывая 0x01 graphic

в ряд и ограничиваясь первыми 2-мя членами разложения, будем иметь

0x01 graphic

или в логарифмическом виде:

0x01 graphic
(2.4)

Учитывая, что при 1 > x > -1

lg(1 + x) = ? x -
? +...,

где ? - переходный модуль от натуральных к десятичным логарифмам.

Напишем:

0x01 graphic
. (2.5)

Величины

называются аддитаментами и обозначаются соответственно A_b, A_a.

Далее обозначим:

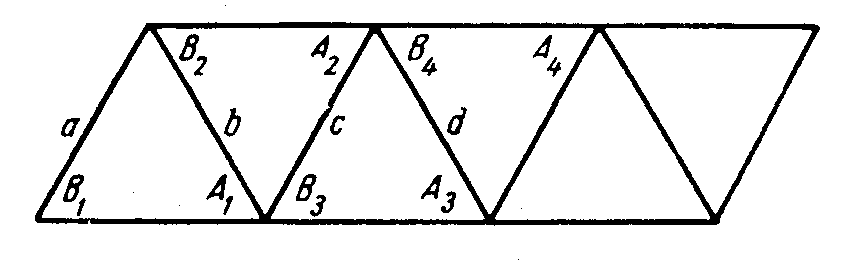
0x01 graphic
(2.6), (2,7)

Пусть имеем цепь треугольников рис. 2.3, тогда

0x01 graphic

Рис. 2.3

0x01 graphic
. (2.8)

Если в логарифм исходной стороны a ввести поправку - A_a, т.е. вычислить lg a?=lg a - A_a и с этим новым значением a? исходной стороны вычислить стороны треугольников, рассматривая их сферические углы как углы плоских треугольников, то получим:

0x01 graphic
. (2.9)

Отсюда вытекает следующий порядок вычислений сторон сферических треугольников по способу аддитаментов:

1) из логарифма исходной стороны вычитается ее аддитамент и таким образом вычисляется 1ga',

2) с исправленным значением логарифма исходной стороны решаются треугольники как плоские без изменений сферических углов, т. е. определяются lg b', lg c', lg d';

3) вычисленные значения lg b', lg c', lg d' исправляют соответственными аддитаментами по формулам (2.9) и получают искомые значения сторон треугольников триангуляции.

Радиус шара, необходимый для вычисления аддитаментов, теоретически должен иметь свое, значение для каждого треугольника, а именно: он должен быть равен среднему радиусу кривизны для средней широты треугольника. Однако практически при вычислении треугольников по способу аддитаментов достаточно получить радиус для некоторой средней точки триангуляции, расстояние которой от крайних треугольников не должно превышать некоторого предела, зависящего от точности вычислений. Найдем это расстояние.

Определим изменение аддитамента в зависимости от изменения R:

0x01 graphic
.

Но

0x01 graphic

Поставив условие, чтобы ошибка в аддитаменте, обусловленная неточностью принятой широты, не превышала 0,5 единицы 8 знака логарифма (т.е. 0x01 graphic

), и положив, что s =50 км (А_s=45?10^-7) получим:

?B © 4®48?.

Следовательно, составив таблицу аддитаментов для какой-либо широты, средней для данной триангуляции, мы можем пользоваться этой таблицей для решения треугольников, отстоящих на 5® по широте к северу и югу от точки с данной широтой. Другими словами, в пределах пояса, ограниченного параллелями, шириной в 1000 км, мы можем не считаться с изменением R₁, если только аддитаменты вычислены для средней широты взятого пояса.

Из выражения

0x01 graphic

следует, что

0x01 graphic
.

В семизначных логарифмических таблицах на каждой странице внизу приводятся величины:

0x01 graphic

где А_x - аддитамент аргумента х, выраженного в секундах, следовательно,

0x01 graphic
.

Таким образом, если стороны треугольников выразить в угловой мере, то аддитаменты можно вычислять, пользуясь указанными логарифмическими таблицами.

Рассмотрим пример решения треугольника по способу аддитаментов.

ПРИМЕР вычисления аддитаментов.

B_m = 47®49?

Элементы формулы	A_a	A_b	A_c
	6.85 963	6.85 963	6.85 963
	6.39 032	6.39 032	6.39 032
2 lgs	9.30 250	9.18 172	9.33 984
lg A_s	2.55 245	2.43 167	2.58 979
A_s	357	270	389

Оставить комментарий © Copyright Мак Петр Анатольевич Размещен: 26/05/2016, изменен: 26/05/2016. 26k. Статистика. Глава: Естествознание Иллюстрации/приложения: 4 шт. Скачать FB2		Ваша оценка:

Мак Петр Анатольевич : другие произведения.

Вг