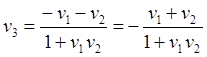Парадокс близнецов - обзор решений,
гл.6 Анализ формулы сложения скоростей
Путенихин П.В.
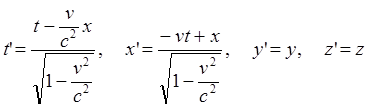 (63.7)
(63.7)
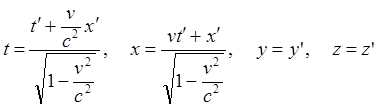 (63.8)
(63.8)
 (64.6)
(64.6)
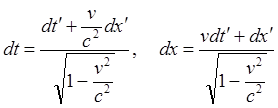
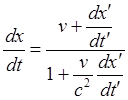 (6.1п)
(6.1п)
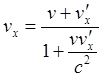 (64.7)"
(64.7)"
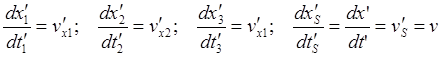 (6.2)
(6.2)
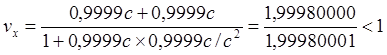
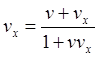 (6.3)
(6.3)
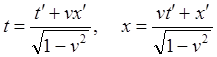
![]() (6.4)
(6.4)
![]()
![]()
![]()
![]()
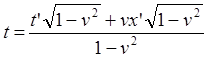
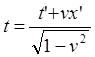
![]()
![]()
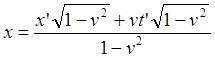
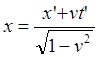
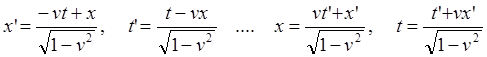
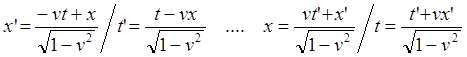
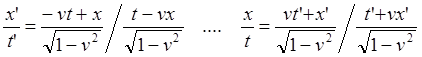
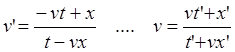
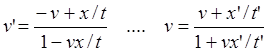
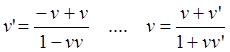
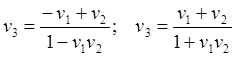
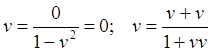 (6.5)
(6.5)
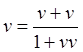
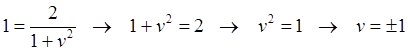
![]()
![]()
![]()
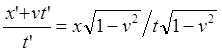
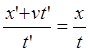
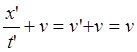

Рис.6.1. Сложение разных скоростей встречно движущихся ИСО
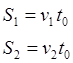
![]()
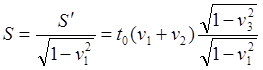
![]()
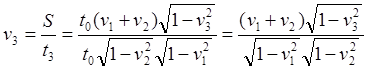 (6.6)
(6.6)
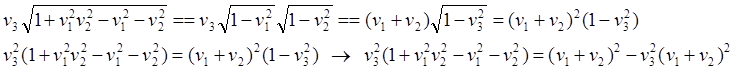
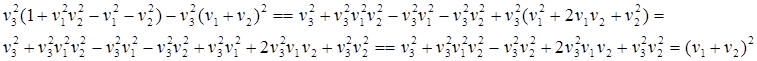
![]()
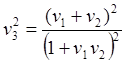
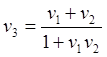 (6.7)
(6.7)
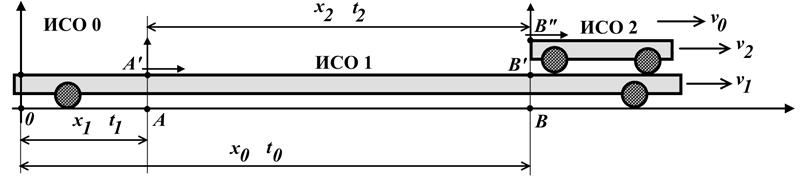
Рис.6.2. Сложение скоростей попутно движущихся ИСО
![]()
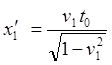
![]()
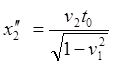
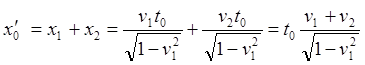
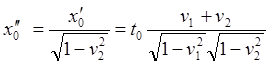
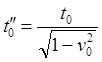
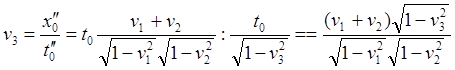
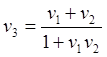
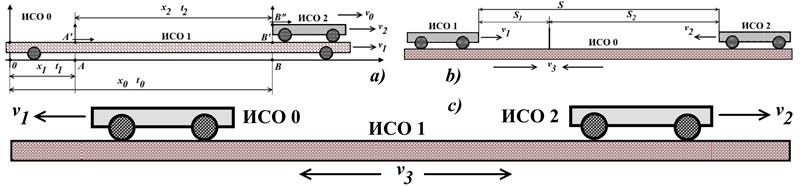
Рис.6.3. a) копия рис.6.2 сложения скоростей попутно движущихся ИСО; b) копия рис.6.1 сложения скоростей сближающихся ИСО; c) преобразование рисунка a) к виду рисунка b) - сложение скоростей удаляющихся друг от друга ИСО