Сыченко Игорь Алексеевич. Расширение собственной формы на основании последовательности Фейгенбаума

И.А. Сыченко

Расширение формулы собственной формы

на основании последовательности Фейгенбаума

(в ответ на работу "Метакод и протокод")

2014*

1. Проблема качественных скачков в познании

Теория исчисления форм предлагает нам способ задания собственной формы через рекурсивную формулу:

х = f(x) (1)

Можно экстраполировать эту формулу на процесс познания, представляя функцию f способом познания, аргумент x - объектом познания, а значение функции - знанием. Процесс познания тоже носит рекурсивный характер, поэтому каждое новое значение на шаге n изменяется по сравнению с предыдущим шагом, однако с определенного шага это изменение становится сначала исчезающе малым, а затем и вовсе неразличимым. В таком случае мы утверждаем, что уже познали объект (и даже познали истину), поскольку сколь долго бы мы его дальше ни познавали, уже не замечаем изменения в понимании.

Если взглянуть на процессы познания более широко, то можно увидеть, что на определенном этапе, когда кажется, что объект познан и ничего нового невозможно выявить, происходит качественный скачок и дальнейшее развитие понимания предмета. Зачастую в таких случаях говорят, что посмотрели под другим углом, открыли новое измерение, подход и т.д.

Откуда в такой схеме берется качественное (а зачастую внезапное и скачкообразное!) изменение в понимании предмета изучения, будь то конкретный единичный объект или социальная система? В рамках формулы (1) появление нового подхода или взгляда под другим углом либо никак не вытекает, либо же скрыто и/или неявно встроено в функцию f.

2. Последовательность Фейгенбаума как аналог собственной формы

В 1975 году Митчелл Фейгенбаум открыл универсальную постоянную, позже названную в его честь. Фейгенбаум работал с последовательностью, которая также была названа его именем. Суть работы заключалась в рекурсивном вызове функции, которая удовлетворяет простым условиям и легко подвергается анализу.

Функция выглядела следующим образом:

f_? [0, 1] - [0, 1]: x ? ?x(1 - x) (2)

Иными словами, присутствует функция:

f(x) = ?x(1 - x) (3)

Здесь ? - нормирующий коэффициент, призванный удержать область значений и определений в заданных рамках [0, 1]. Однако на самом деле его назначение значительно шире и точнее его следует называть бифуркационным параметром. Почему именно так, будет показано ниже.

Для начала рассмотрим n первых шагов рекурсивного вызова функции:

x₁ = f(x₀) = ?x₀(1 - x₀)

x₂ = f(x₁) = f(f(x₀)) = ?x₁(1- x₁)

...

x_n = f(x_n_-₁) = f ⁿ(x₀) = ?x_n-1(1 - x_n_-₁)

Здесь запись f ⁿ означает рекурсивный вызов n раз функции f.

Метод получения нового значения на каждом шаге рекурсивного вызова полностью совпадает с тем, который применяется при исчислении форм. Кроме того, сами функции, описанные формулами (1) и (3) ведут себя идентично.

Как и в случае с процессом познания в последовательности Фейгенбаума на первый взгляд ожидается, что последовательность значений, которые получаются бесконечным рекурсивным вызовом функции f (т.е. при n ? ?) будет сводиться к определенному числу, то есть аттрактору. Обозначим получаемый аттрактор как x_А. Причем, это будет происходить независимо от нормирующего коэффициента ? и x₀, если они удовлетворяют условиям функции.

Например, взяв нормирующий коэффициент ? = 2,5 для формулы (3), мы видим, что бесконечный рекурсивный вызов функции f приводит к значению 0,6 (x_А = 0,6), независимо от того, какое изначальное значение x₀ взято. Такую же картину мы видим при множестве других значений ?.

Однако наши ожидания не оправдываются, если брать значения ? в интервале [3, 4]. При ? = 3 аттрактор теряет свою устойчивость, и вместо единственного значения x_А мы получаем два значения. К примеру, при ? = 3,2, мы заметим, что возникает периодическая орбита с периодом 2, т.е. получаемое значение x колеблется между: x_А? - 0,799 и x_А?? - 0,513. При значении ? = 3,5, функция колеблется между четырьмя значениями: x_А? - 0,395, x_А?? - 0,861, x_А??? - 0,432, x_А???? - 0,883.

Графически всё многообразие получаемых результатов можно отобразить бифуркационной диаграммой:

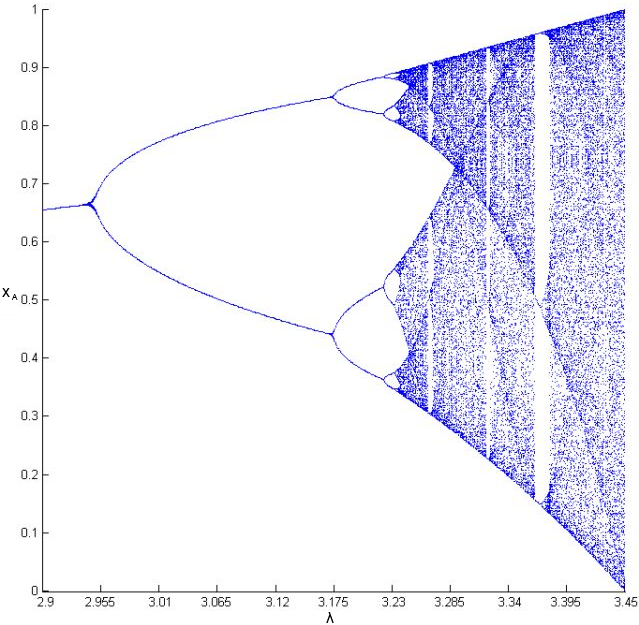
0x01 graphic

Диаграмма показывает появление всего многообразия аттракторов при различных значениях ?. Именно поэтому ? не столько некий "уточняющий" нормирующий коэффициент, а скорее бифуркационный параметр радикально влияющий на x_А.

3. Расширение формулы описания собственной формы

Обратив внимание на формулы (1) и (3), мы сможем заметить между ними явное сходство. В дополнение учтем, что последовательность Фейгенбаума (2) является математическим аналогом процесса проявления собственной формы, описываемой формулой (1).

Попробуем переопределить рекурсивную формулу (1) и функцию f формулы (3), вынося бифуркационный параметр ? за пределы функции. Получим:

x = ? f(x) (4)

где f(x) = x(1 - x).

Теперь отойдем от чисто математического взгляда и вернемся к гносеологической интерпретации формулы (1), которая, очевидно, является частным случаем формулы (4) при ? = 1.

Ранее было сказано, что функция f является функцией (методом) познания, а аргумент x - объектом познания. При бесконечном выполнении функции познания объекта мы получали аттрактор x_А, что в понимании субъекта соответствует истине. С определенного шага это изменение становится настолько исчезающе малым (как это получается и в последовательности Фейгенбаума), что мы вообще можем считать эту истину равной самому объекту x, т.е. в каком-то смысле абсолютным знанием.

Единственный способ сдвинуть процесс познания к принципиально новым содержаниям объекта - это посмотреть на него также под принципиально новым углом зрения (способом познания). Тогда может произойти изменение знания x_А подобная тому, как на изменение x_А влияет бифуркационный параметр?. В результате произойдет качественный скачок в процессе познания. Аналогом подобного изменения ? в познании является смена парадигм, которая и обеспечивает взгляд под новым углом (смену способа познания).

Таким образом, в данном контексте параметр ? играет роль парадигмы, охватывающей разные способы познания и в зависимости от того или иного способа познания кардинально меняющей результат познания, зачастую приводя к неоднозначным выводам вполне в духе диалектики по принципу борьбы и единства противоположностей.

Оглянувшись назад по шкале человеческой истории на путь наук и разума, мы увидим (вслед за Т. Куном), что одна парадигма сменяет другую во времени, поэтому формула (4) является лишь моментальным слепком с длительного, развертывающегося процесса познания. Для того чтобы увидеть процесс в динамике нам потребуется расширить формулу (4), поставить константу ? в зависимость от времени t. Получим:

x = ?(t)f(x) (5)

В определенный момент времени t мы имеем конкретное значение функции ?, то есть конкретное значение ? - математический эквивалент парадигмы с текущими в ней способами познания, поэтому функция ? носит явно гносеологический характер, в то время как функция f - онтологический.

Таким образом, формула (1) является лишь частным случаем и "застывшим" отображением более полной формулы (5).

Как пример, можно привести известную дилемму физиков о природе кванта. В рамках исходной парадигмы в определенный промежуток времени t₁, то есть при ?₁ = ?(t₁), интерпретация результатов опытов приводила к противоположным результатам: одна группа утверждала, что квант имеет корпускулярную природу, другая - волновую (что соответствует x_А? и x_А??^'). Лишь с течением времени по мере приближения к точке бифуркации позиции, принципиально не меняясь, все же сближались через понимание того, что всё не так однозначно. В момент времени t₂ (когда ?₂ = ?(t₂)) произошел качественный скачок, и обе линии сошлись на том, что квант имеет корпускулярно-волновую природу, что привело к появлению теории, описывающей эту природу.

Иной пример, это изучение какого-либо единичного предмета (например, камня) в ретроспективе человеческой истории, когда со временем камень становится орудием труда (первая точка бифуркации), а затем символом (новая точка бифуркации). Далее со временем обе ветви продолжают развиваться независимо, как на бифуркационной диаграмме Фейгенбаума.

Расширяя полученную формулу (5) и вводя новые параметры, мы можем предположить, что функция ? также претерпевает уже парадигмальные изменения, которые зависят от некоторой метафизической функции, или метафункции ?, что позволяет расширить формулу (5) и представить ее в виде частного случая более общей, уже от метарефлексии субъекта s:

x = ?(s)?(x)f(x) (6)

В таком случае ? = ?(s)?(x). Изменения субъекта могут дать новые значения бифуркационного параметра, расширяя его диапазон значений, что в свою очередь даст набор результатов, совершенно невероятный даже без изменения функции ?. Такими примерами метарефлексии субъекта могут быть платоновские идеи, аристотелевская форма форм, плотиновское Единое, кантовские априорные формы, гегелевская абсолютная идея, соловьёвское всеединство и т.п.

Полученная триединая формула (6) удивительным образом пересекается с предложенной С.А. Борчиковым суперпозицией трех функций: трансцендентной (в данном случае на подобную роль претендует функция ?), трансцендентальной (в данном случае аналог - функция ?) и имманентной (аналог - функция f). Функция ? к тому же является отображением гегелевского принципа отрицания отрицания, поскольку возвращает в качестве значения аргумент х - как реализацию функции собственной формы:

x = f*(x) (7)

где f*= ?(s)?(x)f(x).

Таким образом, расширение формулы собственной формы (1) до формул (5) и (6) позволит иначе взглянуть на проблему математического описания собственной формы, в частности на оператор собственной формы f - как на сложную функцию, и приблизить исчисление форм к описанию многообразных процедур познания.

* Игорь Алексеевич Сыченко, участник "Философского семинара" города Озёрска (Сайт семинара - URL: http://philosophy-seminar.ru).

Моисеев В.И. О двух видах собственных форм (eigenforms) [Электронный ресурс]. - URL: http://ru.convdocs.org/docs/index-105101.html

Фейгенбаум М. Универсальность в поведении нелинейных систем // Успехи физических наук. - 1983. - Октябрь. - Т.141, вып.2.

См.: Борчиков С.А. Метакод и протокод. - В наст. издании.

------

127

Оставить комментарий © Copyright Сыченко Игорь Алексеевич (pingvin156@mail.ru) Размещен: 05/07/2015, изменен: 05/07/2015. 14k. Статистика. Статья: Философия Иллюстрации/приложения: 1 шт. Скачать FB2		Ваша оценка:
Аннотация: Статья вышла в издании "Философия в малых формах" (том 6), посвящена такому понятию в исчислении форм как собственная форма, ее связи с процессом познания и проблеме качественных скачков. На основании последовательности Фейгенбаума предложена математическая модель преодоления данной проблемы.

Сыченко Игорь Алексеевич : другие произведения.

Расширение собственной формы на основании последовательности Фейгенбаума