|
|
|
||
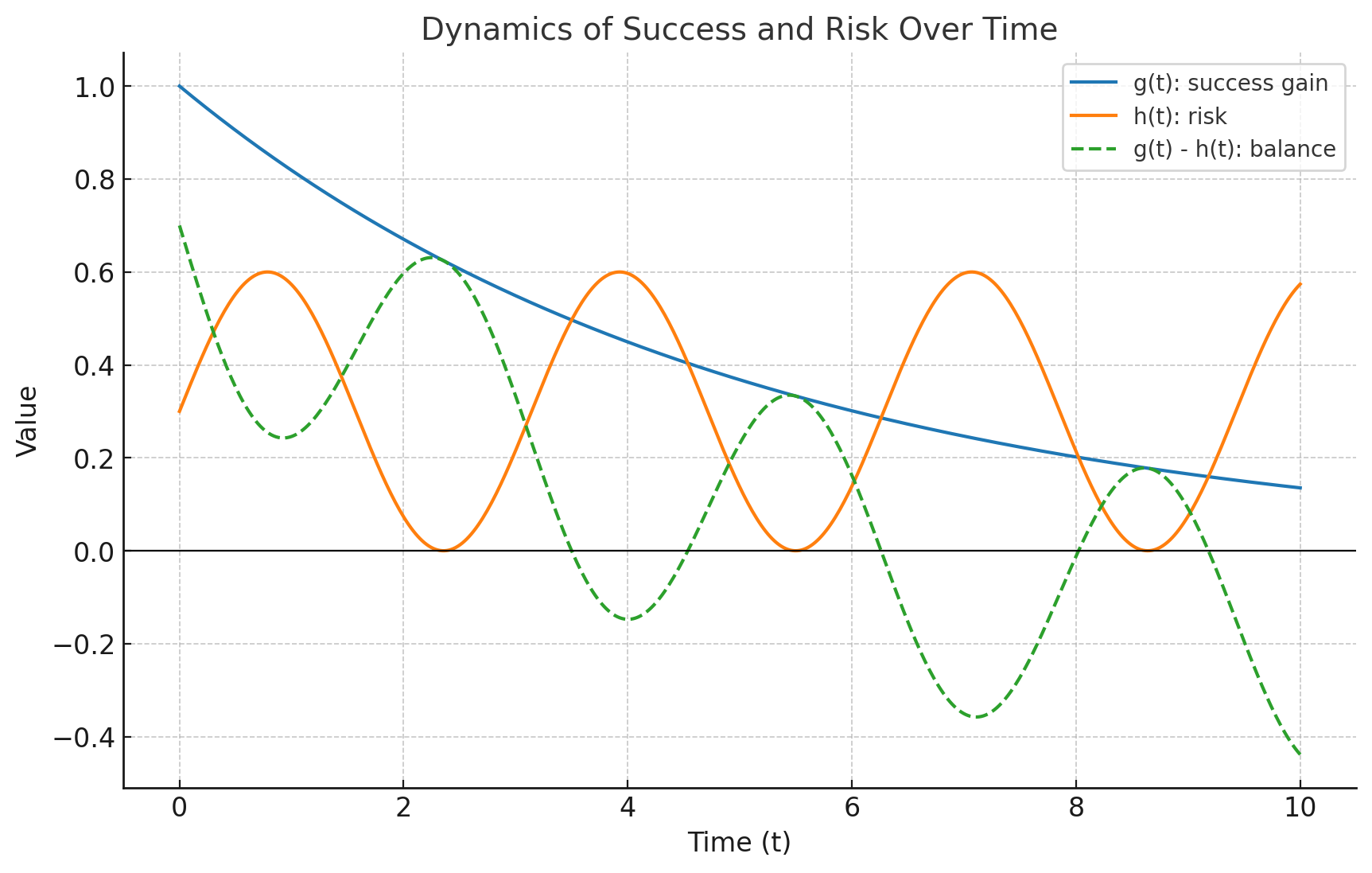
The probability of achieving a goal depends on how the task is broken down into stages and in what order these stages are implemented. This article is devoted to analyzing the optimal selection of the sequence of steps toward the goal.// Andrey A. Angorsky | ||

|