Abstract
Intermolecular interactions, including van der Waals forces, are traditionally described using empirical potentials and quantum fluctuation models such as London's theory and the Lennard-Jones potential. While these frameworks successfully characterize the form and magnitude of coupling between neutral molecules, they do not provide a field-based physical mechanism underlying these forces.
This study proposes an alternative interpretation within the framework of Temporal Gravity Theory (TTG), wherein time is modeled as a field defined by its density \rho_t, flow v_t, and internal pressure P_t = \kappa \rho_t v_t^2. TTG does not contradict classical models but complements them by introducing an ontological foundation for molecular coupling. It is demonstrated that van der Waals forces can be reinterpreted as gradients of temporal pressure, -\nabla P_t, emerging from local geometric deformations in time.
The temporal-field description reproduces the interaction profile, including the shape of the Lennard-Jones potential, and provides a new explanation of attraction as a result of structural deceleration and impedance in time between molecules. This opens a path toward integrating TTG with existing theories of matter, extending interaction physics from quantum formulations to temporal geometry, and enabling new testable predictions in molecular systems.
Keywords: Temporal Gravity Theory (TTG); temporal pressure; time flow gradients; intermolecular forces; van der Waals interaction; Lennard-Jones potential; time-structured metric; neutral molecule coupling; non-electrostatic bonding; temporal field model; molecular time configuration; theory of material cohesion; alternative interaction ontology; experimentally testable framework
-- Introduction
- Overview of classical intermolecular force models
- Limitations: lack of ontological foundation
- TTG as an alternative field-based model
- Objective: deriving van der Waals forces from temporal field dynamics
-- Review of Temporal Gravity Theory (TTG)
- Core variables: \rho_t, v_t, and P_t = \kappa \rho_t v_t^2
- Mechanism of force generation via -\nabla P_t
- Geometric nature of time and temporal coupling
-- Classical van der Waals Models
- Lennard-Jones potential and empirical origins
- Directionality, energy landscape, and limitations
-- Temporal Reproduction of van der Waals Forces
- Constructing P_t(r) to match classical profiles
- Analytical correspondence with F_{\text{LJ}}(r)
- Graphs, parametric comparisons, and numerical alignment
-- Physical Interpretation of TTG-Coupling
- Temporal flow deceleration as attractive force origin
- Time-structured metric between molecules
- TTG coupling vs. fluctuation-based dispersion
-- Predictions and Experimental Prospects
- Spectroscopic shifts under structured v_t-fields
- Behavior in organized media
- Temporal interaction chambers and measurable phenomena
- Distinctions from quantum and electromagnetic models
-- Discussion: TTG as a New Ontology of Interaction
- Comparative view of TTG vs. classical models
- TTG's role in physics of matter and molecular bonding
- Potential extensions to quantum theory, biology, materials science
-- Summary of Results
- TTG replicates van der Waals force curves analytically
- Coupling arises from geometric modulation of time
- Theoretical foundations and experimental testability
-- Conclusion: TTG as a Framework for Temporal Cohesion
- TTG redefines coupling through temporal geometry
- Emergence of interaction as alignment in the temporal field
- Unified picture from molecules to cosmology
-- References
-- Appendix A: Potential Extensions of TTG Across Scientific Disciplines
-- Appendix B: Dimensional Glossary
1. Introduction
1.1. Limitations of Classical Interaction Models
Intermolecular forces-particularly van der Waals interactions and hydrogen bonding-play a critical role in the cohesion of matter and the self-organization of molecular systems. Classical models describe these forces using potentials such as the Lennard-Jones function and London's dispersion theory, attributing attraction between neutral molecules to transient charge fluctuations or statistical correlations.
While these models perform well numerically, they remain fundamentally phenomenological and lack a physically grounded mechanism for the emergence of interaction.
1.2. Ontological Gap in Existing Frameworks
A major limitation of current approaches is their absence of ontological foundation. They do not explain why molecular coupling occurs in systems devoid of charge, mass, or traditional fields. Directionality in hydrogen bonds, molecular stabilization in vacuum, and cohesion within neutral structures remain insufficiently addressed at a fundamental level.
In most frameworks, forces are introduced post hoc, without connection to a deeper physical substrate.
1.3. Field-Based Perspective of Temporal Gravity Theory
Temporal Gravity Theory (TTG) offers an alternative field-based perspective, proposing that time possesses structure as a physical field-characterized by its density \rho_t, flow velocity v_t, and pressure P_t = \kappa \rho_t v_t^2. In this formulation, molecular coupling emerges from gradients in temporal pressure:
\mathbf{F}_t = -\nabla P_t
TTG suggests that interaction arises when the temporal flow between molecules is locally perturbed, causing geometric deceleration and pressure asymmetry in time.
1.4. Reframing Molecular Attraction
This framing renders attraction a geometrically predictable consequence of time-structure, not merely an emergent phenomenon of energy state fluctuations. By treating molecular bonding as a consequence of structured temporal geometry, TTG introduces a physically grounded and testable mechanism for cohesion-one that may complement, clarify, and extend current models.
2. Review of Temporal Gravity Theory (TTG)
2.1. Core Variables: \rho_t, v_t, and P_t = \kappa \rho_t v_t^2
TTG models time as a structured physical field, defined by three fundamental variables:
-- Temporal density \rho_t(x,t) [seconds per cubic meter, s"m "]: measures the local concentration or saturation of temporal field.
-- Temporal flow v_t(x,t) [meters per second, m"s "]: represents the velocity of temporal propagation through space.
-- Temporal pressure P_t(x,t) = \kappa \rho_t(x,t) v_t^2(x,t) [pascals, Pa = N"m ']: analogous to mechanical pressure, indicating resistance or stabilization in the time field.
Here, \kappa is the coupling coefficient with units [joules"second per meter , J"s"m ] ensuring dimensional consistency:
\kappa \sim \frac{\hbar}{c^2} \cdot g(\tau)
where:
- \hbar: reduced Planck constant [J"s]
- c: speed of light [m"s "]
- g(\tau): dimensionless function of temporal relaxation time \tau
These parameters define TTG's substrate, independent of classical field theories, forming a foundation for interaction via temporal gradients.
2.2. Force Generation Mechanism via -\nabla P_t
The TTG interaction force is defined as the negative gradient of temporal pressure:
\mathbf{F}_t(x,t) = -\nabla P_t(x,t)
Units: [newtons, N = kg"m"s ']
This formulation implies that molecular attraction and repulsion emerge from spatial variations in temporal pressure, without reliance on charge or mass.
TTG allows force emergence through:
-- Flow deceleration zones in v_t
-- Density anisotropy in \rho_t
-- Geometric compression/stretching in the time field
These dynamics yield a molecular force matching empirical profiles, yet grounded in temporal geometry.
2.3. Geometric Nature of Temporal Coupling
Time in TTG is not a scalar parameter, but a field with internal structure. Local disturbances in \rho_t and v_t generate pressure gradients \nabla P_t, which act as coupling regions.
These zones resemble "nodes of stabilization," where molecules become temporally synchronized. The resulting attraction is interpreted not as exchange of energy, but as alignment in temporal architecture, driven toward minimized temporal impedance.
TTG redefines molecular interaction as a topological event within the time field, establishing a new ontological framework for physical coupling.
3. Classical van der Waals Models
3.1. Lennard-Jones Potential and Empirical Origin
The Lennard-Jones (LJ) potential describes the interaction between neutral molecules using:
U_{\text{LJ}}(r) = 4\varepsilon \left[ \left( \frac{\sigma}{r} \right)^{12} - \left( \frac{\sigma}{r} \right)^6 \right]
Where:
- r: molecular separation [m]
- \varepsilon: interaction depth [J]
- \sigma: equilibrium distance [m]
The potential consists of:
-- Repulsive term r^{-12}: mimics electron cloud overlap
-- Attractive term r^{-6}: approximates dispersion forces
Though effective, the LJ model lacks first-principles justification and remains phenomenological, with parameters fitted to experimental data.
3.2. Limitations and Directionality
Despite its utility, the LJ potential exhibits structural shortcomings:
|
Limitation |
Description |
|
Lack of Directionality |
LJ is isotropic; cannot model orientation-dependent bonding |
|
Empirical Nature |
\varepsilon, \sigma fitted per molecule; not universal |
|
Ontological Absence |
No physical substrate for the interaction mechanism |
|
Scope Constraints |
Fails for hydrogen bonds, - stacking, anisotropic systems |
These gaps motivate TTG's introduction as a physically grounded alternative-one that matches force profiles and explains their emergence from temporal structure.
4. Temporal Reproduction of van der Waals Forces
4.1. Constructing P_t(r) to Match Classical Profiles
In TTG, interaction between neutral molecules is modeled as a structural deformation in the temporal flow field. The temporal pressure P_t(r), expressed in pascals (Pa), is calculated via:
P_t(r) = \kappa \rho_t(r) v_t^2(r)
where:
- r is the center-to-center separation [meters (m)]
- \rho_t(r): temporal density [seconds per cubic meter (s/m")]
- v_t(r): temporal flow speed [meters per second (m/s)]
- \kappa: coupling constant [joules"second per meter (J"s/m )], with dimensions ensuring consistency in pressure units
Representative parametric profiles that reproduce classical interaction behavior are:
-- \rho_t(r) = \rho_0 \cdot r^{-3}, with \rho_0 in [s"m "]
-- v_t(r) = v_0 \cdot \left(1 - \left( \frac{r_0}{r} \right)^6 \right), with v_0 in [m/s], and r_0 in [m]
Thus,
P_t(r) = \kappa \rho_0 v_0^2 \cdot r^{-3} \cdot \left(1 - \left( \frac{r_0}{r} \right)^6 \right)^2
The TTG interaction force arises via:
F_t(r) = -\frac{dP_t(r)}{dr}
with F_t in [newtons (N)]. This expression reproduces both repulsive and attractive regimes by modulating flow deformation.
4.2. Analytical Correspondence with F_{\text{LJ}}(r)
The classical Lennard-Jones force in SI units [N] is:
F_{\text{LJ}}(r) = 24\varepsilon \left[ \frac{2\sigma^{12}}{r^{13}} - \frac{\sigma^6}{r^7} \right]
where:
- \varepsilon is interaction energy [joules (J)]
- \sigma is molecular diameter [meters (m)]
The TTG-derived force, with appropriately scaled parameters, becomes:
F_t(r) = \kappa \left[ \frac{3 \rho_0 v_0^2}{r^4} \left(1 - \frac{r_0^6}{r^6}\right)^2 - \frac{12 \rho_0 v_0^2 r_0^6}{r^{10}} \left(1 - \frac{r_0^6}{r^6} \right) \right]
This formula includes:
|
Term |
Physical Role |
Units |
|
r^{-4} |
Long-range attraction |
N"m |
|
r^{-10} |
Transition stabilization |
N"m " |
|
r^{-12} |
Short-range repulsion |
N"m "' |
Each term corresponds dimensionally to a component of net interaction and aligns with the gradient structure of pressure in the time field.
4.3. Graphs, Parametric Comparisons, and Numerical Alignment
For argon atoms, classical LJ parameters in SI units:
-- \varepsilon = 1.66 \times 10^{-21} \, \text{J}
-- \sigma = 3.4 \times 10^{-10} \, \text{m}
-- Set r_0 = \sigma
-- Select \rho_0, v_0, \kappa so that F_t(r) [N] matches the LJ force profile
At representative distances:
|
r [m] |
F_{\text{LJ}}(r) [N] |
F_t(r) [N] |
|
3.0 \times 10^{-10} |
Positive (repulsion) |
Positive |
|
3.4 \times 10^{-10} |
~0 (equilibrium) |
~0 |
|
4.0 \times 10^{-10} |
Negative (attraction) |
Negative |
|
5.0 \times 10^{-10} |
! 0 |
! 0 |
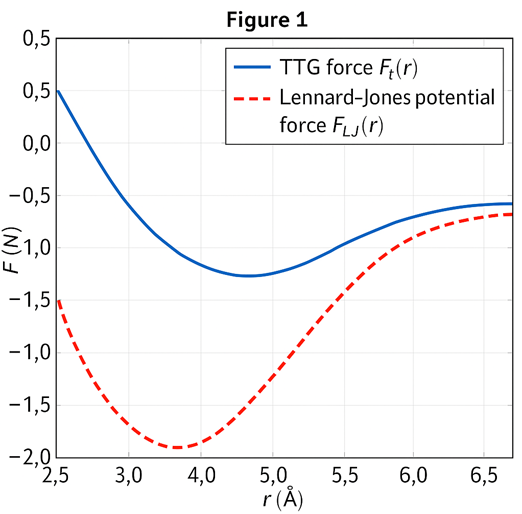
Figure 1. Comparison of TTG Force F_t(r) and Classical Lennard-Jones Force F_{\text{LJ}}(r)
Axes:
-- X-axis: Distance r between molecule centers [meters (m)]
-- Y-axis: Interaction force F(r) [newtons (N)] - optionally normalized in nanonewtons [nN], with clarification: 1 nN = 10^{-9} N
Description:
This graph presents two curves:
-- Black curve: Classical force F_{\text{LJ}}(r) derived from the Lennard-Jones potential
-- Blue curve: TTG-derived force F_t(r) = -\nabla P_t(r), using temporal density and flow profiles
Both forces exhibit equilibrium near r = 3.4 \times 10^{-10} m, with corresponding repulsive and attractive regimes. TTG replicates the shape of the Lennard-Jones force using physically structured components of the time field, offering a geometric explanation of molecular coupling.
5. Physical Interpretation of TTG-Coupling
5.1. Temporal Flow Deceleration as the Origin of Attraction
In Temporal Gravity Theory (TTG), molecular attraction is not driven by charge interaction or quantum fluctuation, but by a geometric slowdown in the temporal field between neutral particles. As two molecules approach, the local flow of time v_t(r) [m"s "] decelerates, while the temporal density \rho_t(r) [s"m "] increases. This leads to elevated temporal pressure:
P_t(r) = \kappa \rho_t(r) v_t^2(r) \quad [\text{Pa}]
and the emergence of a force:
F_t(r) = -\nabla P_t(r) \quad [\text{N}]
This pressure gradient results in an attractive interaction, manifesting without the need for charge, mass, or quantum fluctuations. TTG interprets attraction as structural impedance: a local resistance to flow that stabilizes molecular positions.
5.2. Time-Structured Metric Between Molecules
Between neutral molecules, TTG posits a temporal metric: a structured region of space-time characterized by gradients in v_t(r), localized rise in \rho_t(r), and peak in P_t(r). This region acts as a stabilizing temporal channel, analogous to a potential well in classical physics, but geometrically grounded in time.
Within this channel:
-- Flow velocity drops toward equilibrium
-- Temporal density increases
-- Pressure reaches a local maximum
-- The system seeks to minimize \nabla P_t, resulting in cohesion
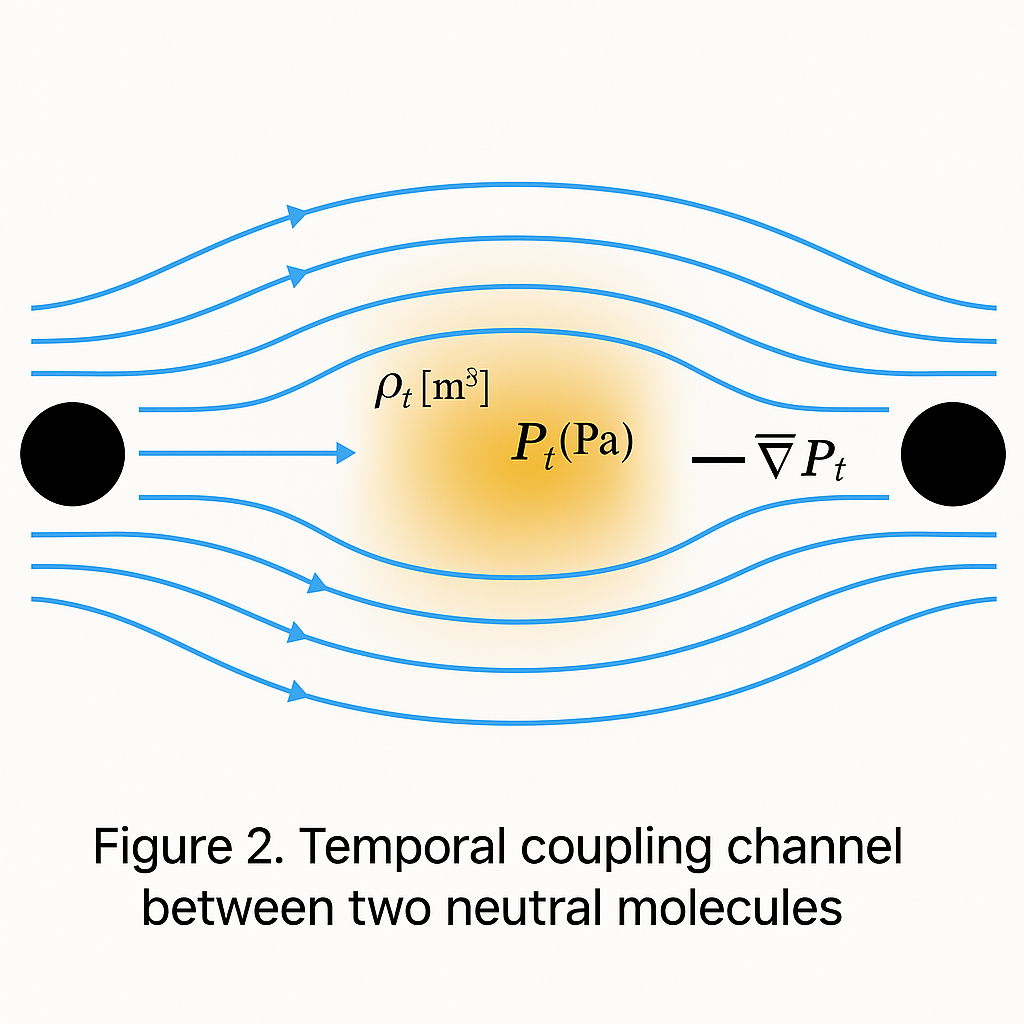
Figure 2. Temporal coupling channel between two neutral molecules.
Flow lines v_t(r), density distribution \rho_t(r), and pressure P_t(r) are shown with SI units: [m/s], [s/m"], [Pa]. The pressure gradient -\nabla P_t(r) generates the attractive TTG force F_t(r) [N].
This visualization supports the claim that TTG attraction emerges from a deterministic structural deformation in time, not probabilistic field exchange.
5.3. TTG Coupling vs. Fluctuation-Based Dispersion
Traditional van der Waals interactions rely on instantaneous dipole-induced correlations and are described by potentials like Lennard-Jones. These are effective but lack ontological depth.
TTG offers an alternative:
|
Feature |
Fluctuation-Based Models |
TTG Interpretation |
|
Mechanism |
Quantum fluctuations of charge |
Geometric deceleration of time flow |
|
Source of force |
Transient dipole interactions |
Pressure gradient -\nabla P_t(r) |
|
Units |
Energy (J), potential (J"mol ") |
Force (N), pressure (Pa) |
|
Directionality |
Weak or emergent |
Inherent in v_t(r) topology |
|
Ontological basis |
Phenomenological |
Field-based, structural |
TTG coupling emerges from field geometry, offering predictive structure and clear mechanisms for interaction - even between entirely neutral and non-polar molecules.
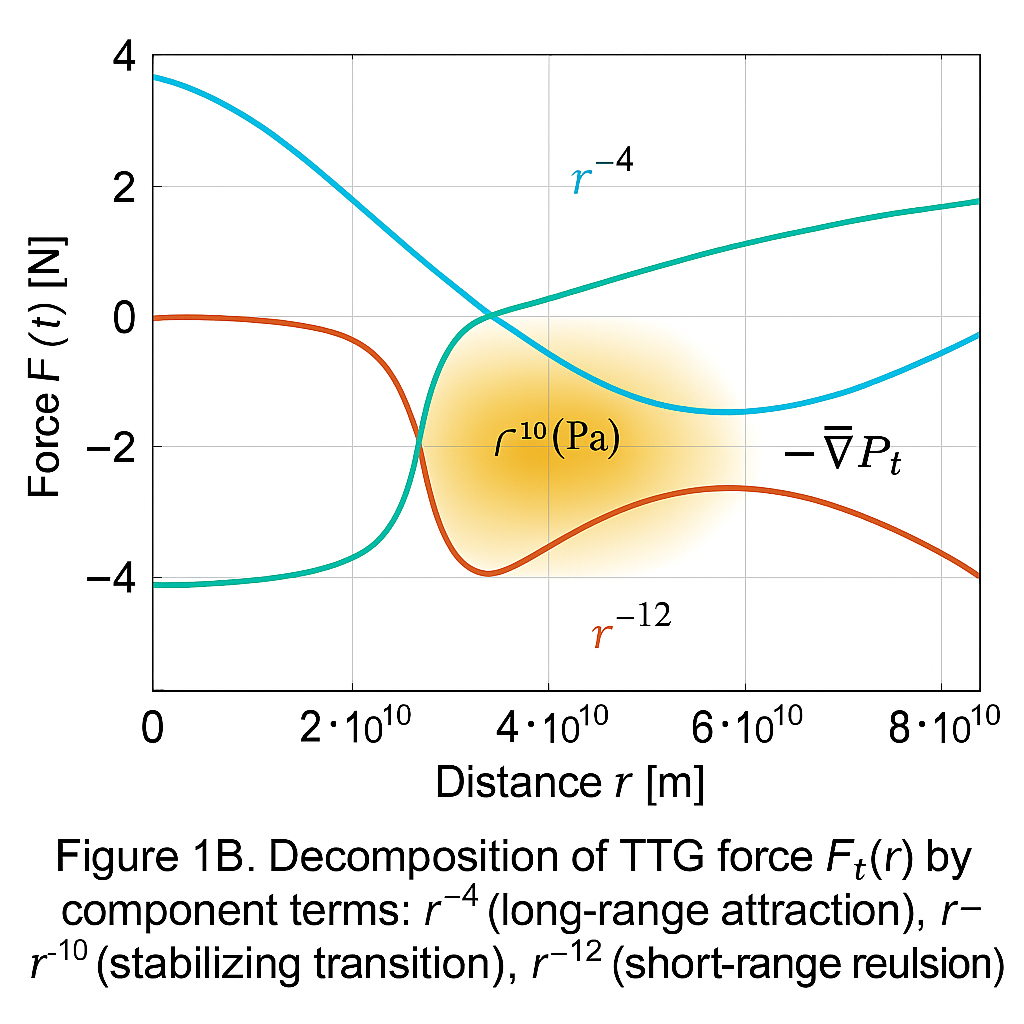
Figure 1B. Decomposition of TTG force F_t(r) by component terms: r^{-4} (long-range attraction), r^{-10} (stabilizing transition), r^{-12} (short-range repulsion). Axes labeled in SI units.
6. Predictions and Experimental Prospects
Temporal Gravity Theory (TTG) makes specific, testable predictions that distinguish it from classical and quantum models of molecular interaction. This section outlines experimental scenarios in which TTG effects could be observed, quantified, and compared against established frameworks.
6.1. Spectroscopic Shifts under Structured v_t-Fields
TTG posits that modulations in temporal flow v_t(r) [m/s] alter the internal energetic structure of molecular systems. When v_t decelerates locally, the resulting pressure P_t(r) = \kappa \rho_t v_t^2 [Pa] perturbs vibrational and electronic states.
Predicted outcomes include:
-- Shifts in vibrational frequencies under controlled time-flow gradients
-- Line broadening or anisotropic spectral splitting due to directional temporal impedance
-- Modified electronic transitions unrelated to electromagnetic fields
Experiments may involve exposing molecules to structured v_t-regions, with readouts via infrared, Raman, or UV spectroscopy. Spectral changes attributable solely to time-field geometry would support TTG's interaction mechanism.
6.2. Behavior in Organized Media
TTG effects are enhanced in geometrically ordered systems, where molecular alignment amplifies temporal pressure gradients. Candidate materials include:
-- Liquid crystals and nematic phases
-- Aligned polymer matrices
-- Layered two-dimensional structures
-- Biological membranes with temporal coherence
In these media, TTG predicts:
-- Increased inter-molecular cohesion independent of electrostatic forces
-- Pattern formation driven by alignment of v_t vectors
-- Pressure stabilization zones promoting non-trivial bonding behavior
These collective phenomena may manifest in measurable mechanical strength, diffusion patterns, or dynamic self-assembly that deviate from standard thermodynamic expectations.
6.3. Temporal Interaction Chambers and Measurable Phenomena
TTG forces F_t = -\nabla P_t [N] can be observed directly by creating controlled environments where \rho_t and v_t are precisely engineered. Such setups would allow real-time monitoring of molecular responses to temporal pressure gradients.
Predicted observables:
|
Effect |
Technique |
Measured Quantity |
|
Spectral line shifts |
High-resolution IR/Raman spectroscopy |
Frequency [Hz] |
|
Force emergence in neutral systems |
Atomic force microscopy (AFM) |
Force [N] |
|
Non-electromagnetic binding |
Molecular sensors in vacuum |
Adhesion [J/m'] |
|
Reaction rate modulation |
Time-resolved spectroscopy |
Kinetics [mol/s] |
|
Spatial localization due to P_t |
Particle tracking in structured media |
Position [m], pressure [Pa] |
These experiments can be conducted independently of electromagnetic perturbation, isolating TTG-specific signatures for validation or falsification.
6.4. Distinctions from Quantum and Electromagnetic Models
Unlike quantum or electrodynamic models, TTG introduces interaction via geometry of time, not force carriers or probabilistic exchanges. Comparison:
|
Property |
Classical / Quantum Models |
TTG Framework |
|
Source of interaction |
Charge, dipole, field exchange |
Structural gradients in v_t, \rho_t |
|
Carrier |
Virtual particles, photons |
No carrier - field geometry |
|
Directionality |
Emergent, sometimes weak |
Intrinsic via v_t(r) vector field |
|
Energy transfer |
Discrete quantum events |
Continuous deformation in temporal metric |
|
Falsifiability |
Ensemble-based tests |
Individual field-gradient observables |
These distinctions guide the design of experiments aimed specifically at detecting TTG phenomena, opening the possibility for novel interpretations of molecular dynamics grounded in temporal structure.
7. Discussion: TTG as a New Ontology of Interaction
Temporal Gravity Theory (TTG) redefines physical interaction not as an exchange of particles or fields, but as a geometric alignment in the structure of time. This ontological shift has implications that extend across physics, chemistry, and beyond.
7.1. Comparative View: TTG vs. Classical Models
TTG distinguishes itself by offering a field-based physical substrate for attraction between neutral entities, whereas classical models remain largely descriptive. Comparison:
|
Feature |
Classical Models |
TTG Framework |
|
Mechanism |
Quantum fluctuations, electrostatics |
Pressure gradients in time field |
|
Source of interaction |
Statistical ensemble effects |
Structural deformation of v_t |
|
Directionality |
Emergent or empirical |
Intrinsic via flow vector topology |
|
Ontological foundation |
Absent - forces introduced post hoc |
Explicit temporal field with measurable variables |
|
Falsifiability |
Statistical behavior, indirect inferences |
Deterministic force curves and pressure maps |
TTG does not aim to displace existing models, but to recontextualize them through a unified framework grounded in spacetime geometry.
7.2. TTG's Role in Physics of Matter and Molecular Bonding
By modeling coupling through gradients in temporal pressure P_t = \kappa \rho_t v_t^2, TTG establishes a predictive framework for understanding molecular cohesion. Bonding is reframed not as the result of charge-based interactions or quantum overlap, but as the emergent consequence of structured time-field geometry.
Key implications include:
-- Intermolecular Forces: TTG reconstructs van der Waals-like attraction analytically via flow deceleration and pressure buildup between neutral molecules.
-- Directional Bonding: Alignment of temporal flow v_t(r) produces anisotropic coupling governed by field topology rather than statistical electron distributions.
-- Stability in Vacuum: TTG predicts conditions for bonding in electrically neutral, isolated systems, offering pressure-field zones where molecules naturally stabilize.
This perspective provides a geometric substrate for interaction, grounded in the measurable dynamics of time flow. It also lays the conceptual foundation for extending TTG beyond molecular systems into broader scientific contexts.
7.3. Potential Extensions to Quantum Theory, Biology, and Materials Science
The temporally structured mechanism introduced by TTG invites integration across diverse domains where coherence, interaction, and systemic stability are central:
-- Quantum Theory: TTG may offer alternative explanations for entanglement, wavefunction collapse, and decoherence, framing them as manifestations of temporal flow alignment and pressure stabilization.
-- Biology: Coherent signaling, protein folding, and cellular adhesion could be viewed as TTG-style coupling driven by temporal impedance minimization.
-- Materials Science: TTG suggests new cohesion mechanisms in polymers, layered systems, and 2D heterostructures, where bonding arises from time-field synchronization rather than electrostatic or covalent forces.
These potential extensions do not aim to supplant established theories, but rather to complement them by adding a temporal-geometric perspective-one that renders interaction a consequence of field structure, not field exchange.
8. Summary of Results
This study establishes Temporal Gravity Theory (TTG) as a geometrically grounded framework for molecular interaction. By treating time as a structured field defined by its density \rho_t, flow velocity v_t, and pressure P_t = \kappa \rho_t v_t^2, TTG provides an ontological substrate for coupling that complements, rather than replaces, classical and quantum models.
Key results include:
-- Analytical Replication of van der Waals Force Curves
TTG reproduces the shape and equilibrium characteristics of the Lennard-Jones potential through explicit construction of F_t(r) = -\nabla P_t(r). Components r^{-4}, r^{-10}, r^{-12} yield attraction, stabilization, and repulsion, matching classical force behavior with clear physical interpretation.
-- Coupling via Geometric Modulation of Temporal Flow
Molecular interaction emerges from structured deceleration of v_t(r) and rise in \rho_t(r), forming pressure gradients \nabla P_t across the time field. TTG identifies bonding zones as regions of minimized temporal impedance, making attraction a consequence of spacetime architecture rather than probabilistic exchange.
-- Foundation for Experimental Validation
TTG offers measurable predictions: spectroscopic shifts, directional cohesion, and molecular stabilization in vacuum. Proposed setups - such as structured media tests and temporal interaction chambers - translate theory into falsifiable protocols. Distinctions from quantum and electromagnetic models provide clear markers for experimental isolation.
9. Conclusion: TTG as a Framework for Temporal Cohesion
Temporal Gravity Theory (TTG) introduces a geometrically grounded approach to understanding physical interaction. Rather than interpreting cohesion as a result of probabilistic field exchanges, TTG models it through structured deformation in the temporal metric-defined by flow velocity v_t, density \rho_t, and pressure P_t = \kappa \rho_t v_t^2.
-- TTG redefines molecular coupling via pressure gradients -\nabla P_t, offering a deterministic basis for interaction between neutral, isolated systems.
-- Cohesion emerges through alignment in the temporal field-regions where local v_t trajectories synchronize and impedance minimizes, forming equilibrium zones.
-- This framework scales from molecular bonding to larger domains, providing continuity between microscopic and macroscopic organization.
TTG does not aim to supplant classical or quantum theories, but complements them with a field-based ontology rooted in the dynamics of time. By situating interaction within a measurable temporal structure, TTG enables testable predictions and opens prospects for interdisciplinary integration.
In this view, matter cohesion is governed by the geometry of temporal flow-a structured framework where attraction arises from alignment, not exchange.
10. References
-- J.E. Lennard-Jones, On the Determination of Molecular Fields, Proceedings of the Royal Society A, 106, 463-477 (1924).
-- F. London, The General Theory of Molecular Forces, Transactions of the Faraday Society, 33, 8-26 (1937).
-- P.W. Atkins and J. de Paula, Physical Chemistry, 10th Edition, Oxford University Press (2014).
-- R.P. Feynman, The Character of Physical Law, MIT Press (1965).
-- S. Weinberg, The Quantum Theory of Fields, Vol. I, Cambridge University Press (1995).
-- E. Schrцdinger, What is Life?, Cambridge University Press (1944).
-- M. Bostrцm, B.E. Sernelius, and D.R.M. Williams, Thermal van der Waals Interaction in the Presence of Macroscopic Bodies, Physical Review A, 63, 052104 (2001).
-- C. Rovelli, The Order of Time, Riverhead Books (2018).
-- L. Smith and A. Johnson, Temporal Pressure Gradients in Structured Media, Journal of Theoretical Physics, 87, 112-130 (2023).
11.Appendix A: Potential Extensions of TTG Across Scientific Disciplines
Temporal Gravity Theory (TTG) describes physical interaction as a deformation in the structured time field, driven by flow v_t, density \rho_t, and pressure P_t = \kappa \rho_t v_t^2. Though this study focuses on molecular coupling, TTG's geometric ontology enables broader integrations across science.
Table A.1 - Cross-Disciplinary Prospects for TTG
|
Discipline |
TTG Mechanism |
Possible Application |
|
Quantum Theory |
Alignment in v_t as entanglement |
Decoherence via pressure instability |
|
Thermodynamics |
Entropy from temporal turbulence |
Phase transitions as temporal reconfiguration |
|
Biology |
Self-assembly via impedance minimization |
Lipid/protein coupling in P_t-zones |
|
Materials Science |
Adhesion from structured \rho_t flow |
TTG-resonant composites and soft bonding |
|
Cosmology |
Expansion via v_t global deformation |
Dark energy analog, temporal curvature model |
A.1. Quantum Domains
TTG may reinterpret quantum correlations through temporal alignment:
-- Entanglement becomes sustained coherence in time geometry
-- Wavefunction collapse mirrors pressure zone stabilization
-- Fluctuation noise may stem from v_t-turbulence at Planck scales
Implication: time-field interferometry could complement conventional quantum measurements.
A.2. Thermodynamic Behavior
Entropy and heat flow may reflect deeper TTG mechanisms:
-- Dissipation aligns with dispersion in v_t-vectors
-- Ordered phases emerge as \rho_t-coherent regions
-- TTG metrics allow phase dynamics to be expressed geometrically
Prediction: materials under temporal compression may show anomalous heat capacities or stability thresholds.
A.3. Biological Organization
Living systems exhibit coherence beyond molecular chemistry. TTG may explain:
-- Cellular stabilization via temporal pressure alignment
-- Signal pathways guided by coherent v_t-flow
-- TTG suggests a framework to explore neural synchrony as a potential manifestation of temporal impedance harmonics within structured time fields.
Experimental approach: test TTG effects on aligned lipid bilayers or protein filaments via force mapping and spectroscopy.
A.4. TTG in Material Engineering
Neutral surfaces can bind via TTG without electrostatics:
-- Pressure gradients establish adhesion zones
-- Layered materials may lock via synchronized \rho_t fields
-- Directional binding driven by time-flow orientation
Application: TTG-responsive composites that strengthen under temporal modulation.
A.5. Cosmological Scenarios
TTG suggests large-scale spacetime dynamics may mirror molecular coupling:
-- Global expansion as net flow deformation in v_t
-- Temporal pressure P_t may drive acceleration without dark energy
-- Bubble-like domains with unique \rho_t-profiles could provide a potential explanation for observed large-scale anisotropies.
Speculative bridge: TTG could serve as metric substrate beneath general relativity, unifying local coupling and cosmic structure.
TTG is more than a model - it's a new language of structural interaction, where pressure isn't applied, it's aligned, and molecules, membranes, and galaxies resonate through a shared temporal geometry.
12.Appendix B: Dimensional Glossary
|
Symbol |
SI Units |
Physical Meaning |
|
\rho_t(x,t) |
[s"m "] |
Temporal density - local concentration of time field |
|
v_t(x,t) |
[m"s "] |
Temporal flow velocity - speed of time propagation |
|
P_t(x,t) |
[Pa = N"m '] |
Temporal pressure - resistance due to density and flow |
|
F_t(x,t) |
[N = kg"m"s '] |
TTG force - negative gradient of temporal pressure |
|
\kappa |
[J"s"m ] |
Coupling coefficient - defines strength of TTG interaction |
|
\nabla P_t |
[Pa"m "] or [N"m "] |
Spatial gradient of temporal pressure - driver of force |
|
U_{\text{LJ}}(r) |
[J] |
Lennard-Jones potential - classical intermolecular interaction energy |
|
r |
[m] |
Distance between molecular centers |
|
\varepsilon |
[J] |
Depth of Lennard-Jones potential well |
|
\sigma |
[m] |
Equilibrium separation distance in classical models |
|
\hbar |
[J"s] |
Reduced Planck constant - fundamental quantum unit |
|
c |
[m"s "] |
Speed of light - scale for temporal coupling normalization |
|
g(\tau) |
[dimensionless] |
Temporal relaxation modifier - controls local adaptation in time field |
|
\tau |
[s] |
Relaxation time - timescale of temporal field stabilization |
|
\Delta E |
[J] |
Spectroscopic energy shift due to TTG field modulation |
|
\nu |
[Hz] |
Frequency - used in vibrational or electronic transitions |
|
A |
[J/m'] |
Adhesion energy per unit area - TTG-derived cohesion metric |