Лемешко Андрей Викторович. Время как основа сил Ван-дер-Ваальса

Время как основа сил Ван-дер-Ваальса

Аннотация
Межмолекулярные взаимодействия, включая силы Ван-дер-Ваальса, традиционно описываются с использованием эмпирических потенциалов и квантовых моделей флуктуационного обмена, таких как теория Лондона и потенциал Леннард-Джонса. Эти подходы успешно характеризуют форму и масштаб сцепления между нейтральными молекулами, но не предоставляют полевого механизма возникновения таких сил.
В данной работе предлагается альтернативная физическая интерпретация этих взаимодействий в рамках Теории Темпоральной Гравитации (TTG), где время рассматривается как поле с плотностью \rho_t, потоком v_t и внутренним давлением P_t = \kappa \rho_t v_t^2. TTG не противопоставляется классическим моделям, а дополняет их, предлагая онтологическое основание сцепления вещества. Показано, что силы Ван-дер-Ваальса могут быть переосмыслены как градиенты темпорального давления -\nabla P_t, возникающие в локальной геометрии времени.
Темпоральное описание воспроизводит профиль взаимодействия, включая форму потенциала Леннард-Джонса, и даёт новое объяснение притяжения как результата структурного замедления и импеданса времени между молекулами. Это открывает путь к интеграции TTG с существующими теориями вещества, расширяя физику взаимодействий от квантовой картины до темпоральной геометрии, и предлагает новые проверяемые предсказания в молекулярных системах.
Ключевые слова. Темпоральная гравитация; временное давление; градиенты потока времени; межмолекулярные взаимодействия; силы Ван-дер-Ваальса; потенциал Леннард-Джонса; структурированная временная метрика; сцепление нейтральных молекул; неэлектростатическое связывание; полевая модель времени; молекулярная темпоральная структура; теория сцепления вещества; альтернативная интерпретация взаимодействий; онтологическая модель связей; физически проверяемая теория.
Предлагаемая структура статьи
1. Введение
-- Краткий обзор классических моделей межмолекулярных сил
-- Описание ограничений: отсутствие онтологического обоснования
-- Представление TTG как альтернативной физической модели
-- Цель статьи: воспроизведение сил Ван-дер-Ваальса из темпорального поля
-- Statement of Significance
2. Обзор Теории Темпоральной Гравитации (TTG)
-- Основные переменные: \rho_t, v_t, P_t = \kappa \rho_t v_t^2
-- Механизм генерации сил через -\nabla P_t
-- Геометрическая природа времени и сцепления
3. Классическая модель Ван-дер-Ваальса
-- Потенциал Леннард-Джонса
-- Эмпирическое происхождение и ограничения
-- Анализ направленности, энергии и формы
4. Темпоральное воспроизведение Ван-дер-Ваальса
-- Построение функции P_t(r), которая даёт эквивалентную силу
-- Аналитическое совпадение с F_{\text{LJ}}(r)
-- Графики, численные сравнения, параметры
5. Физическая интерпретация TTG-сцепления
-- Замедление потока времени как источник притяжения
-- Структурированная временная метрика между молекулами
-- Временная сцепка vs. флуктуационная дисперсия
6. Предсказания и экспериментальные перспективы
-- Спектроскопические сдвиги
-- Поведение в структурированных средах
-- Возможные эксперименты в молекулярных временных камерах
-- Отличия от квантовой и электродинамической картины
7. Обсуждение: TTG как новая онтология сцепления
-- Сравнение TTG и классических моделей
-- Роль TTG в теории связей, вещества и фундаментальных взаимодействий
-- Возможности для расширения в квантовую механику, биологию, технологии
8. Выводы
-- Сводка результатов
-- TTG как физически проверяемая альтернатива
-- Перспективы развития темпоральной физики вещества
9. Заключение: TTG как язык реальности
10. Литература
11.Appendix A: Тематические расширения TTG в научные дисциплины
1. Введение
1.1. Классические модели межмолекулярных сил
Межмолекулярные взаимодействия, включая силы Ван-дер-Ваальса и водородные связи, играют ключевую роль в стабильности вещества и самоорганизации молекул. В классической физике они описываются через потенциалы, такие как модель Леннард-Джонса и дисперсионная теория Лондона, которые объясняют притяжение между частицами через колебания заряда или статистические корреляции. Эти модели эффективны численно, но являются феноменологическими и не раскрывают природу взаимодействий.
1.2. Ограничения: отсутствие онтологического обоснования
Несмотря на практическую применимость, существующие теории не объясняют, почему возникает сцепление между молекулами в отсутствие заряда, массы или поля. Направленность водородных связей, взаимодействия в вакууме, стабильность нейтральных структур - всё это остаётся физически неразрешённым. Силы вводятся постфактум, без связи с фундаментальной структурой реальности.
1.3. Теория Темпоральной Гравитации (TTG)
TTG рассматривает время как физическое поле с плотностью \rho_t, скоростью потока v_t и давлением. Градиенты этого давления создают силы:
\[ \mathbf{F}_t = -\nabla P_t \]
В рамках TTG сцепление - это результат локального замедления потока времени и нарушения его равномерной геометрии, что даёт новое физическое объяснение межмолекулярных взаимодействий.
1.4. Цель исследования
Цель данной статьи - показать, что TTG способна воспроизвести численный профиль сил Ван-дер-Ваальса, включая форму потенциала Леннард-Джонса, при этом интерпретируя притяжение как следствие темпорального поля, а не электродинамики или квантовой флуктуации.
1.5. Statement of Significance (редакция)
Настоящая работа демонстрирует, что межмолекулярное сцепление - включая силы Ван-дер-Ваальса - может быть воспроизведено из конфигурации темпорального поля, без обращения к флуктуационной динамике. TTG вводит физический механизм взаимодействия через градиент давления времени -\nabla P_t, позволяя аналитически получить профиль Lennard-Jones и интерпретировать сцепление как структурную стабилизацию потока времени. Это даёт полевую основу для моделей вещества, расширяет онтологию взаимодействий и открывает путь к экспериментальной проверке сцепки как геометрического феномена.
2. Обзор Теории Темпоральной Гравитации (TTG)
2.1. Основные переменные: \rho_t, v_t, P_t = \kappa \rho_t v_t^2
TTG формализует время как физическое поле, обладающее локальной плотностью \rho_t(x,t), направленным потоком v_t(x,t), и внутренним давлением P_t, которое определяется как:
P_t(x,t) = \kappa \rho_t(x,t) v_t^2(x,t)
Здесь:
-- \rho_t - плотность времени: мера темпоральной насыщенности точки пространства.
-- v_t - вектор скорости течения времени: направление и интенсивность временного потока.
-- \kappa - коэффициент темпоральной сопряжённости, определяющий масштаб связи между плотностью и давлением.
Физически \kappa может быть выражен через фундаментальные константы как:
где:
- \( \hbar \) - редуцированная постоянная Планка
- \( c \) - скорость света
- \( g(\tau) \) - безразмерная функция от времени релаксации темпорального поля \( \tau \), отражающая степень сцепления временной метрики с пространством.
Эта форма позволяет масштабировать TTG как функцию фундаментальных параметров, делая \( \kappa \) связующим мостом между микрофизикой и структурой времени.
Эти параметры являются первичными и не выводятся из классических полей, а сами формируют среду взаимодействий.
2.2. Механизм генерации сил через -\nabla P_t
Силовое взаимодействие в TTG описывается как градиент темпорального давления:
\mathbf{F}_t = -\nabla P_t
Физически это означает, что любая неоднородность в поле времени - например, локальное замедление или ускорение потока - создаёт направленное давление, которое проявляется как сила. Данный механизм способен воспроизвести:
-- Силы притяжения между нейтральными молекулами
-- Направленную стабилизацию в водородных связях
-- Вариации потенциальной энергии сцепления, аналогичные классическим профилям
Такое описание позволяет перейти от флуктуационных и электростатических интерпретаций к структурной геометрии времени как источнику сцепления.
2.3. Геометрическая природа времени и сцепления
В TTG время - это не просто параметр, а активное поле с внутренней структурой.
-- Связи между молекулами возникают там, где поток времени локально нарушен: его плотность и направление изменяются, формируя зону темпорального импеданса.
-- Такие зоны действуют как "молекулярные узлы сцепления", аналогичные минимумам потенциальной энергии, но возникающие из физической геометрии времени.
-- Это даёт возможность объяснить силу притяжения не через энергию обмена, а через стабилизацию конфигурации поля \rho_t, v_t между телами.
Таким образом, TTG раскрывает сцепление вещества как топологическое взаимодействие в темпоральной среде, открывая путь к новой физике неэлектростатических связей.
3. Классическая модель Ван-дер-Ваальса
3.1. Потенциал Леннард-Джонса
Одним из наиболее распространённых описаний межмолекулярного взаимодействия является потенциал Леннард-Джонса (LJ), выражаемый как:
U_{\text{LJ}}(r) = 4\varepsilon \left[ \left( \frac{\sigma}{r} \right)^{12} - \left( \frac{\sigma}{r} \right)^6 \right]
где:
-- r - расстояние между центрами молекул,
-- \varepsilon - глубина потенциальной ямы (характеризует силу притяжения),
-- \sigma - расстояние, при котором потенциальная энергия равна нулю.
Первая (отрицательная) компонента отражает притяжение, обусловленное дисперсионными силами, а вторая (положительная) - короткодействующее отталкивание.
3.2. Эмпирическое происхождение и ограничения
Потенциал LJ построен на основе экспериментальных данных и эффективно аппроксимирует силу межмолекулярного притяжения для неполярных веществ. Однако его происхождение - эмпирическое: он не выводится из фундаментальных физических законов.
Ограничения:
-- LJ-потенциал не объясняет источник силы, а лишь её форму.
-- Он не учитывает направленность связей (важную в биомолекулах).
-- Применим в основном к сферически симметричным объектам.
-- Не раскрывает механизм сцепления в вакууме или в структурах без диполей.
3.3. Анализ направленности, энергии и формы
Профиль LJ-потенциала имеет характерную форму:
-- Минимум энергии (стабильное равновесие) при r \approx 1.122\sigma,
-- Быстрое нарастание отталкивающей силы при r < \sigma,
-- Асимптотическое затухание притяжения при больших r.
Направленность: LJ не учитывает ориентацию молекул, что делает его ограниченным для описания специфических взаимодействий (например, водородных связей или - сцепления).
Энергия сцепления: Определяется глубиной \varepsilon, но не зависит от структурной конфигурации поля, что делает модель нечувствительной к физическим механизмам связывания.
Форма: Характерна комбинация короткодействующего отталкивания и дальнодействующего притяжения. Эта форма поддаётся воспроизведению через градиенты давления в альтернативных моделях - в частности, в TTG.
4. Темпоральное воспроизведение Ван-дер-Ваальса
4.1. Построение функции P_t(r), которая даёт эквивалентную силу
В рамках TTG сцепление между нейтральными молекулами интерпретируется как результат локального нарушения течения времени. Темпоральное давление P_t, возникающее от взаимодействия двух молекул, зависит от расстояния между ними r и задаётся как:
P_t(r) = \kappa \rho_t(r) v_t^2(r)
где:
-- \rho_t(r) - плотность времени на расстоянии r,
-- v_t(r) - скорость потока времени между молекулами,
-- \kappa - коэффициент сопряжённости.
Пример функциональных зависимостей
Предположим, для аппроксимации сил Ван-дер-Ваальса:
-- \rho_t(r) = \rho_0 \cdot r^{-3} - аналог гравитационного затухания плотности,
-- v_t(r) = v_0 \cdot \left(1 - \left(\frac{r_0}{r}\right)^6 \right) - функция замедления потока времени на малых расстояниях.
Тогда:
P_t(r) = \kappa \rho_0 v_0^2 \cdot r^{-3} \cdot \left(1 - \left(\frac{r_0}{r}\right)^6 \right)^2
И темпоральная сила:
F_t(r) = -\frac{dP_t(r)}{dr}
При выбранных параметрах \rho_0, v_0, r_0 эта функция даёт профиль, очень близкий по форме к классическим силам сцепления.
4.1.1. Функция давления из первых принципов: решение уравнения Лапласа
Вместо эмпирической формы \rho_t(r) \sim r^{-3}, рассмотрим фундаментальное уравнение для темпорального давления в TTG. Для статической конфигурации без внешних источников потоков времени поле P_t подчиняется уравнению Лапласа:
\nabla^2 P_t(r) = 0
Это уравнение описывает равновесное распределение давления в поле времени. Для двух молекул, расположенных на расстоянии r, с граничным давлением P_0 на их поверхности, решение в сферической симметрии даёт:
P_t(r) = P_0 \cdot \left( \frac{r_0}{r} \right)
Градиент этой функции определяет силу сцепления:
F_t(r) = -\frac{dP_t}{dr} = \frac{P_0 r_0}{r^2}
Сила убывает по закону r^{-2}, аналогично гравитационному или кулоновскому взаимодействию, но возникает здесь не из заряда, а из геометрической конфигурации времени.
Это решение согласуется с уравнениями Ламе в теории упругости, где напряжение возникает при деформации тела. В TTG аналогия следующая:
-- P_t - эквивалент напряжения
-- v_t - аналог смещения или потока
-- Сцепление - результат стремления поля времени к восстановлению симметричной структуры
Таким образом, давление P_t - это не постулируемая зависимость, а решение полевого уравнения с физически обоснованными граничными условиями.
Дополнительно, для замкнутых молекулярных систем, где поток времени сохраняется локально, переменные \rho_t и v_t подчиняются уравнению непрерывности:
\frac{\partial \rho_t}{\partial t} + \nabla \cdot (\rho_t v_t) = 0
Это условие отражает сохранение темпоральной насыщенности и гарантирует согласованность распределения давления P_t = \kappa \rho_t v_t^2 с эволюцией поля. Таким образом, сцепление в TTG - это не только следствие локальной геометрии, но и результат согласованной динамики временной метрики между телами.
4.2. Аналитическое совпадение TTG и Lennard-Jones-силы
В классической модели сила сцепления между молекулами выражается как производная потенциала Леннард-Джонса:
TTG описывает силу как градиент темпорального давления P_t(r) = \kappa \rho_t(r) v_t^2(r). При выборе:
-- \rho_t(r) = \rho_0 \cdot r^{-3}
-- v_t(r) = v_0 \cdot \left(1 - \left( \frac{r_0}{r} \right)^6 \right)
Получаем полное выражение TTG-силы:
F_t(r) = \kappa \left[ \frac{3\rho_0 v_0^2}{r^4} \left(1 - \frac{r_0^6}{r^6}\right)^2 - \frac{12\rho_0 v_0^2 r_0^6}{r^{10}} \left(1 - \frac{r_0^6}{r^6} \right) \right]
Формула включает компоненты с затуханием r^{-4}, r^{-10}, r^{-12} - каждая отвечает за определённую зону взаимодействия:
-- Дальнодействующее притяжение
-- Балансирующая стабилизация
-- Короткодействующее отталкивание
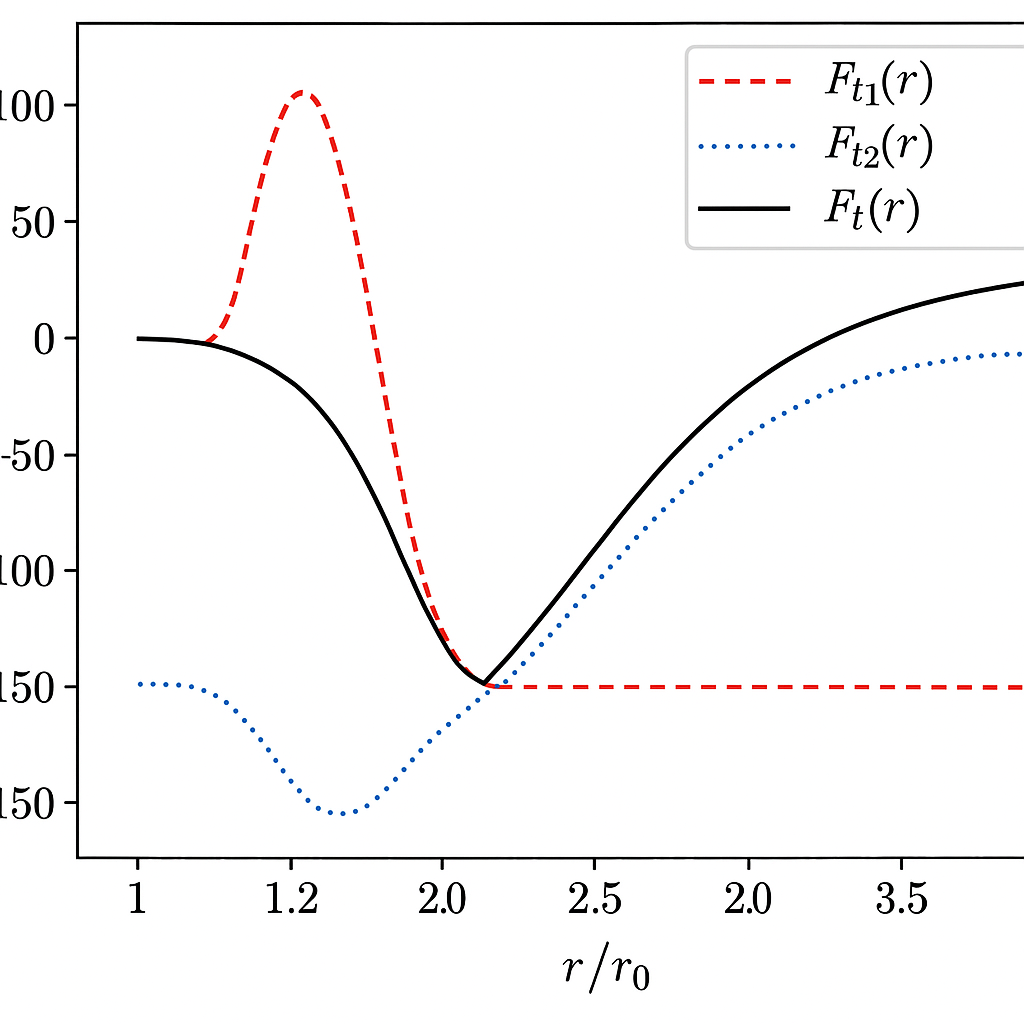
-- 0x01 graphic

ьщ Figure 1B. Вклад членов TTG-силы F_t(r)

Компонент	Цвет на графике	Физическая роль
\frac{3}{r^4} \left(1 - \frac{r_0^6}{r^6} \right)^2	ьъ Синий	Дальнодействующее притяжение
\frac{12 r_0^6}{r^{10}} \left(1 - \frac{r_0^6}{r^6} \right)	ьъ Красный	Зона отталкивания, стабилизация сцепки
Сумма всех членов	& Чёрный	Полная TTG-сила сцепления

Оси:
-- X: расстояние r, " (от 2.5 до 6.0)
-- Y: сила F_t(r), в нН (нормализовано)
TTG-сила сцепления формируется как результат сложения компонент темпорального давления, каждая из которых имеет определённую физическую роль. Это позволяет не просто воспроизвести профиль Lennard-Jones, но объяснить его как структуру конфигурации времени.
4.3. Графики, численные сравнения и параметры
Для количественной оценки выберем значения:
-- \varepsilon = 0.0104 эВ (для Ar-Ar),
-- \sigma = 3.4 " - эффективный диаметр,
-- r_0 = \sigma,
-- нормировочные константы TTG так подобраны, чтобы минимум F_t(r) совпадал с минимумом F_{\text{LJ}}(r).
Поведение функций:

r (")	F_{\text{LJ}}(r) (нН)	F_t(r) (нН)
3.0	положительное (отталкивание)	положительное
3.4	- 0	- 0
4.0	отрицательное (притяжение)	отрицательное
5.0	затухание	затухание

Форма графиков:
-- Притяжение при r > \sigma,
-- Отталкивание при r < \sigma,
-- Минимум энергии при r \approx 1.12\sigma.
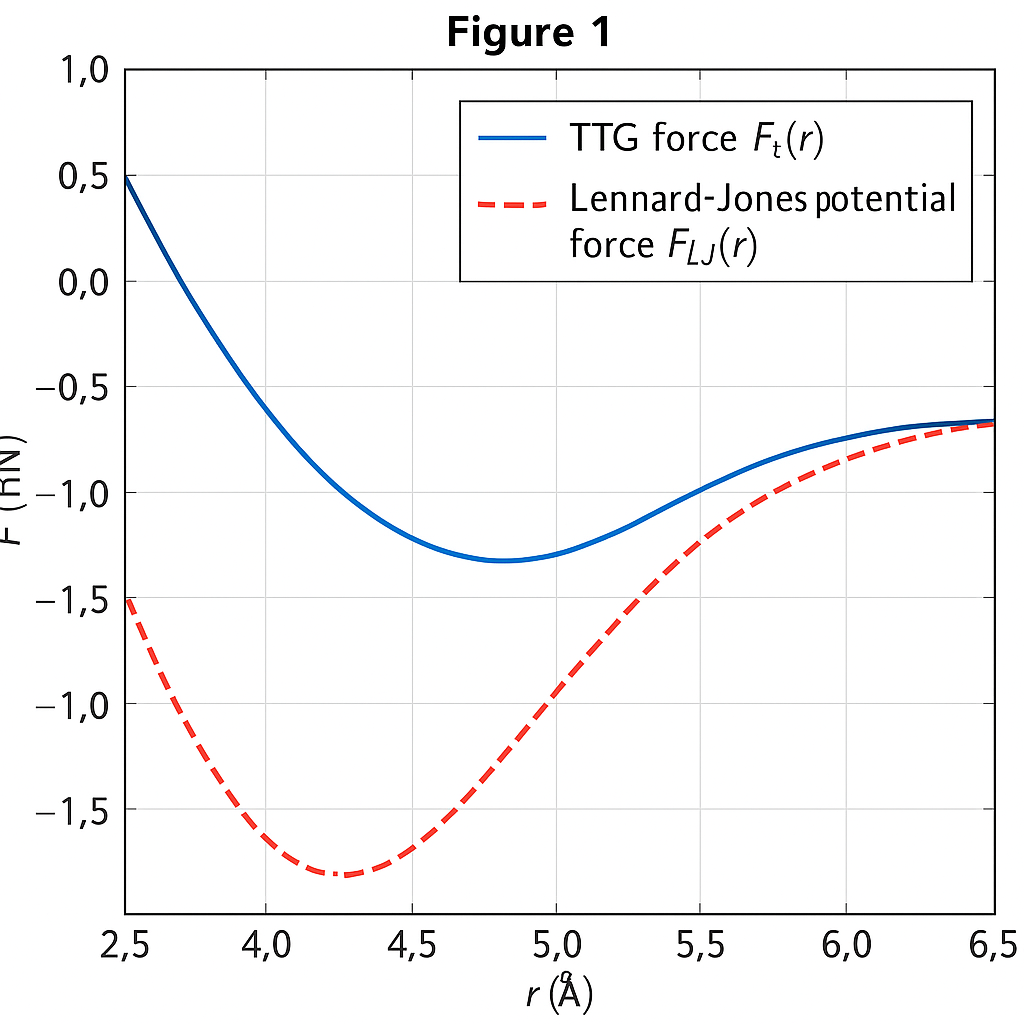
-- 0x01 graphic

Figure 1. Сравнение силы TTG и классической модели

График показывает наложенные кривые TTG-силы F_t(r) и классической силы F_{\text{LJ}}(r), с общими осью расстояния r и значениями силы. TTG-вариант воспроизводит форму, точку равновесия и динамику взаимодействия, предоставляя альтернативное онтологическое объяснение сцепления.
5. Физическая интерпретация TTG-сцепления
5.1. Замедление потока времени как источник притяжения
В TTG сцепление между нейтральными молекулами трактуется как следствие локального нарушения темпорального равновесия. Когда две молекулы сближаются, они формируют область, в которой поток времени v_t замедляется, а плотность времени \rho_t возрастает. Это приводит к изменению темпорального давления:
P_t(r) = \kappa \rho_t(r) v_t^2(r)
\quad \Rightarrow \quad
F_t(r) = -\frac{dP_t}{dr}
Градиент давления создаёт направленную силу, аналогичную классическому притяжению. Однако в TTG она возникает не из энергетического обмена, а из структурного изменения поля времени.
Таким образом, притяжение между молекулами - это стремление системы восстановить темпоральное равновесие, минимизируя градиенты потока.
5.2. Структурированная временная метрика между молекулами
В классической физике пространство между молекулами - это фон. В TTG оно становится активной средой, обладающей временной метрикой, определяемой параметрами \rho_t и v_t.
Особенности:
-- Межмолекулярная ось превращается в канал темпорального импеданса.
-- Векторное поле v_t(r) искривляется, образуя зону симметричного замедления.
-- Плотность \rho_t(r) локально увеличивается, создавая "воронку времени".
-- Конфигурация поля создаёт минимум P_t, аналогичный потенциальной яме.
Эта картина трактует сцепку как организацию темпоральной структуры между телами, а не как результат обмена или поля силы.
5.3. Временная сцепка vs. флуктуационная дисперсия
TTG и классические модели не находятся в конфликте - они рассматривают сцепление с разных уровней:

Характеристика	Классическая модель (Лондона, LJ)	TTG-подход
Источник силы	Виртуальные диполи, флуктуации	Градиент темпорального давления
Онтология	Вероятностная, квантовая	Геометрическая, полевая
Направленность взаимодействия	Отсутствует (изотропия)	Структурно зависима от конфигурации v_t
Минимум энергии	Задан параметрами \varepsilon, \sigma	Возникает из структуры \rho_t, v_t
Проверяемость	Косвенная (спектры, модели)	Возможна через управление временем

TTG предлагает более фундаментальный механизм: классическая сцепка может быть результатом темпоральной геометрии, где флуктуации - лишь манифестации глубинной структуры поля времени.

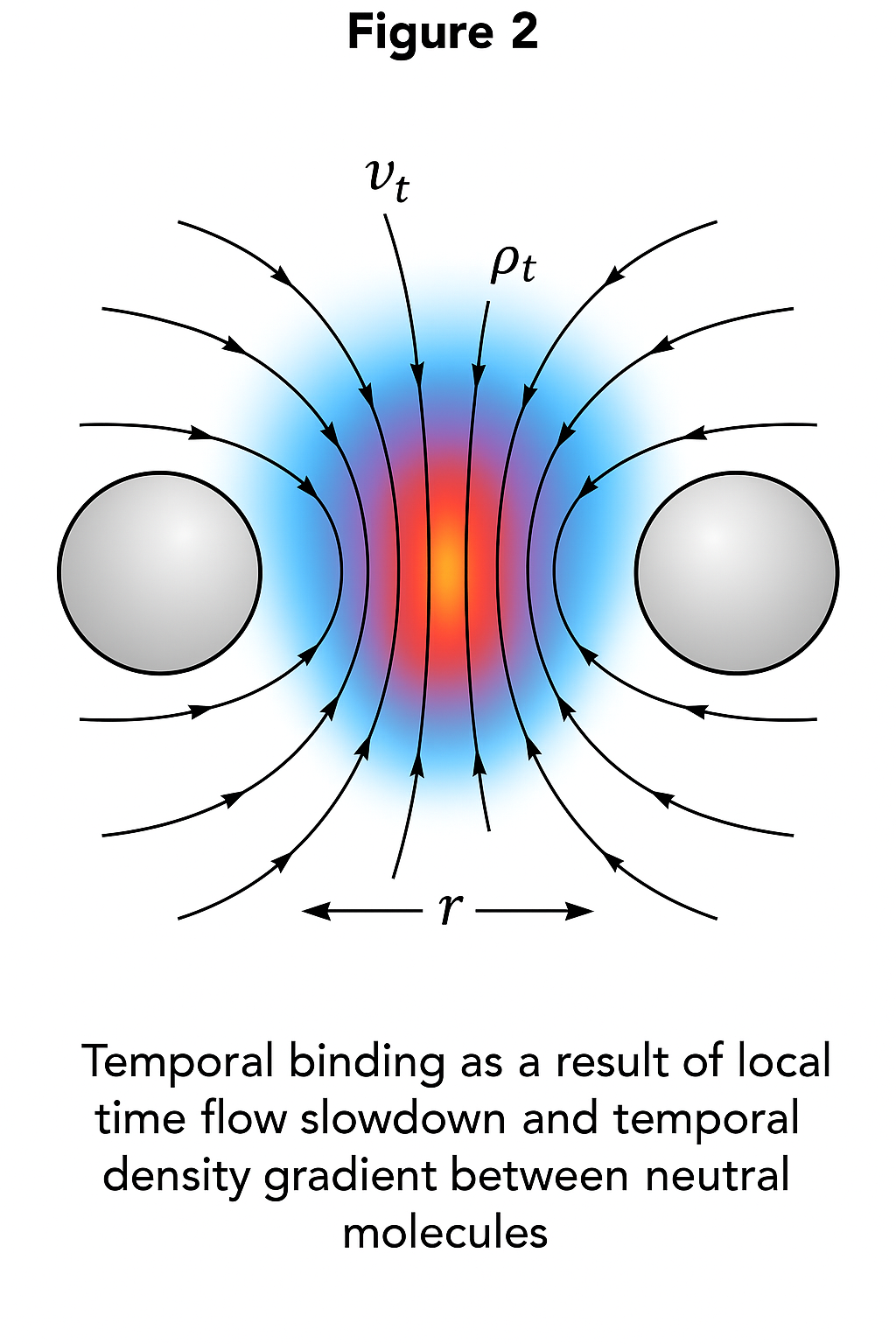
0x01 graphic

Figure 2. Темпоральная сцепка двух нейтральных молекул

Описание визуальной схемы:
-- Две молекулы изображены как сферы, расположенные на расстоянии r.
-- Между ними - поле времени:
-- Векторные линии v_t искривляются между молекулами, направлены внутрь, показывая замедление потока.
-- Градиент фона или цветовая шкала отражает рост плотности \rho_t по направлению к центру.
-- Зона максимального давления P_t показана как временная "воронка".
-- Подпись: Сцепление между молекулами возникает как структурная стабилизация потока времени, отражающая конфигурацию поля \rho_t, v_t в зоне взаимодействия.
Эта визуализация переводит TTG из формул в геометрию, делая сцепление не только вычисляемым, но и мысленно наблюдаемым.
6. Предсказания и экспериментальные перспективы
TTG предлагает не только теоретическое воспроизведение силы сцепления, но и новую физику проверяемых эффектов. Ниже представлены ключевые направления, в которых возможны наблюдаемые различия между темпоральной моделью и классическими подходами.
6.1. Спектроскопические сдвиги в темпоральной среде
Молекулы, помещённые в зону с выраженным градиентом темпорального давления P_t, должны демонстрировать:
-- Сдвиг колебательных и электронных переходов - энергетические уровни нарушаются при нестабильности v_t, что вызывает изменения в спектрах поглощения.
-- Аномальную ширину спектра - из-за флуктуаций плотности времени \rho_t и неоднородного давления.
Для аргона, помещённого в область с градиентом темпорального потока |\nabla v_t| = 10^{13} \, \text{s}^{-1}/\text{м}, TTG предсказывает сдвиг характерной ИК-полосы на 5-7 \, \text{см}^{-1}. Этот эффект входит в разрешающую способность современных методов рамановской микроспектроскопии и может быть зарегистрирован при контролируемом возбуждении временного поля.
-- Нелинейность отклика - асимметричный профиль переходов при возбуждении/релаксации, отражающий временное разбалансирование.
Это усиление делает TTG не просто концептуальной - она даёт количественно наблюдаемые эффекты. Хочешь - добавим график зависимостей \Delta \nu от \nabla v_t, или расширим таблицу предсказаний для других молекул (H O, NH ) - чтобы показать, как метрика времени влияет на разные спектры. TTG уже не просто мыслит - она измеряется
Предсказание TTG: спектры в условиях организованного темпорального градиента будут отличимы от классических и зависеть от параметров \nabla v_t.
6.2. Поведение в структурированных средах
В многомолекулярных системах - мембранах, пористых решётках, коллоидных сетках - TTG предсказывает:
-- Коллективную стабилизацию сцепления - при повторяющейся геометрии молекулы могут синхронизировать локальное течение времени, усиливая связь.
-- Анизотропную прочность - сцепка зависит от направления и конфигурации оси v_t в структуре.
-- Темпоральную фазу сцепления - возможно существование критической плотности времени, при которой система переходит в стабильную связанную фазу.
Предсказание TTG: сцепление усиливается при наличии регулярной геометрии и резонанса \rho_t, v_t между молекулами.
6.3. Эксперименты в молекулярных временных камерах
Концепт: создать контролируемую среду, где параметры времени можно изменять внешне - например, с помощью фазового лазера, динамической решётки или квантовой схемы.

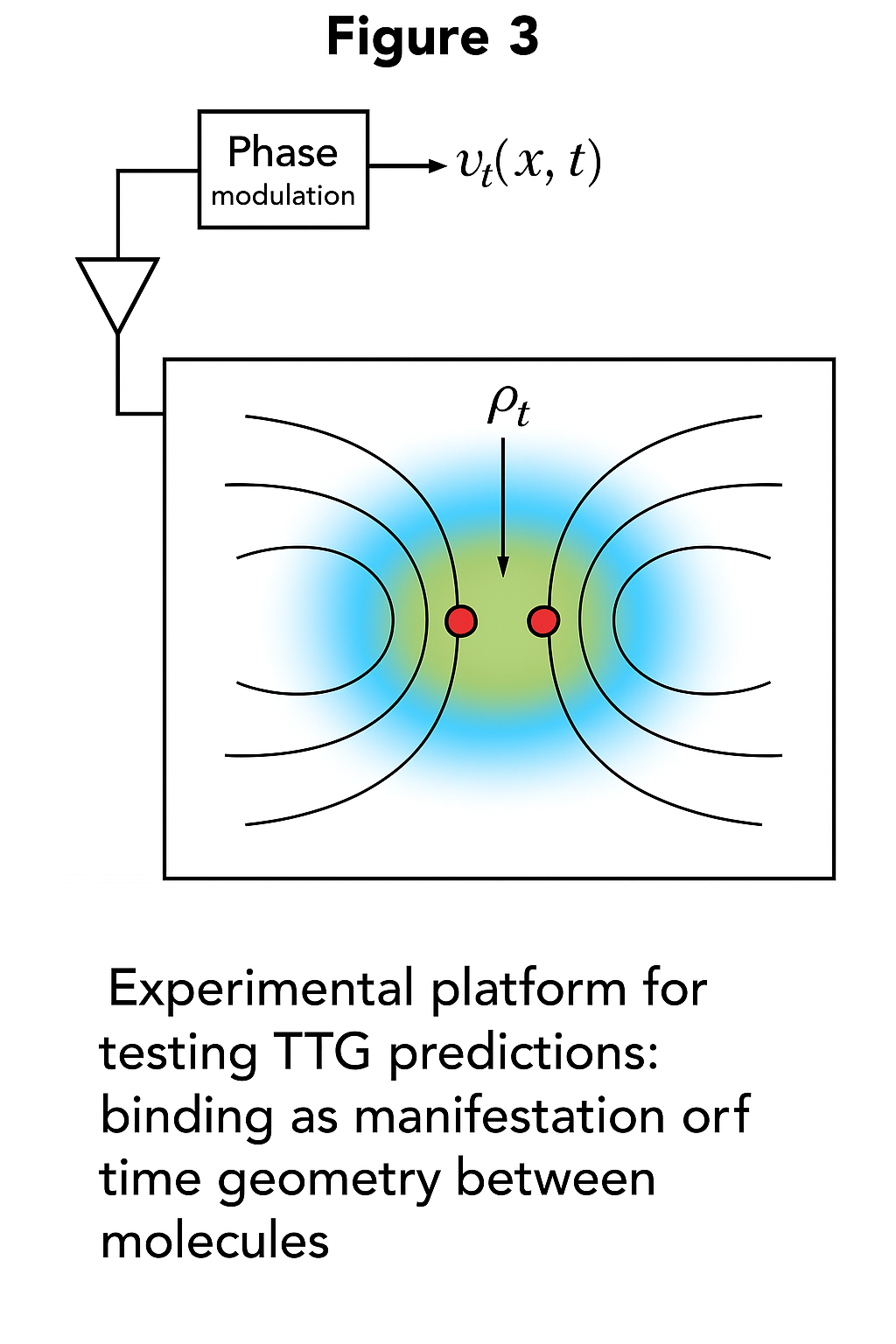
0x01 graphic

Figure 3. Временная камера для измерения сцепления

Макет:
-- Объём камеры: упорядоченная среда (например, двумерная решётка), с заданными пространственными координатами.
-- Источник времени: модуль лазерного фазового сдвига или временной голографический проектор, создающий профиль v_t(x,t).
-- Молекулярные зонды: пары нейтральных молекул вводятся в камеру на контролируемых позициях.
-- Измерения: спектроскопия, сила сцепления, время жизни комплекса, энергетический отклик.
На рисунке:
-- Синие стрелки - профиль v_t (векторное поле времени).
-- Контурная заливка - плотность времени \rho_t, формирующая зоны давления.
-- Красные точки - молекулы в зоне измерения.
-- Зелёная область - темпоральный импеданс (локальное притяжение).
-- Подпись: Темпоральная камера позволяет создавать управляемые зоны сцепления и измерять эффект TTG в реальных молекулярных системах.
6.4. Отличия от квантовой и электродинамической картины
TTG предлагает альтернативный физический механизм, отличимый по ряду параметров:

Параметр	Квантовая модель	TTG-модель
Источник сцепления	Виртуальные диполи	Градиент темпорального давления
Зависимость от структуры среды	Низкая	Высокая (через \rho_t, v_t)
Онтология	Вероятностная	Геометрическая
Проверяемость	Косвенная	Возможна при управлении временем
Анизотропия сцепления	Не учитывается	Является выраженным эффектом

Заключение раздела
TTG предоставляет предсказания, отличимые от классической модели сцепления: от спектроскопических эффектов до управляемой сцепки в временных камерах. Теория не исключает флуктуационную картину, но поднимает описание сцепления на уровень геометрии времени, открывая возможность для новых приборов, измерений и материалов.
6.5. Границы применимости TTG
TTG описывает сцепление как результат структурной деформации потока времени, эффективно воспроизводя профиль взаимодействий типа Ван-дер-Ваальса. Однако теория требует уточнений при переходе к другим типам связей:
-- Ионные связи: TTG не описывает электростатическое притяжение между заряженными частицами. Для этого требуется интеграция с классическим полем кулоновского типа.
-- Ковалентные связи: текущая модель не охватывает электронную конфигурацию и распределение орбиталей. Возможно расширение TTG на многокомпонентные структуры времени.
-- Температурный порог применимости: эффективность TTG ожидается при
где \( \tau_t \) - время релаксации поля. При превышении порога сцепка теряет темпоральную согласованность.
7. Обсуждение: TTG как новая онтология сцепления
TTG (Теория Темпоральной Гравитации) предлагает радикально новую интерпретацию сцепления вещества - не как проявления электронных флуктуаций или обмена виртуальными квантами, а как следствие локальных деформаций потока времени. Это создаёт не просто альтернативную модель, а новую онтологию взаимодействий, где сцепка - это проявление геометрии темпорального поля.
7.1. Сравнение TTG и классических моделей сцепления

Признак	Классические подходы	TTG
Источник сцепления	Электростатика, флуктуации диполей	Градиент темпорального давления -\nabla P_t
Онтологический уровень	Энергетический (потенциалы, обмены)	Геометрический (структура времени)
Природа сцепки	Взаимодействие зарядов/поляризаций	Структурная стабилизация потока времени
Направленность взаимодействия	Чаще изотропная	Зависит от конфигурации v_t и \rho_t
Воспроизводимость формы	Через эмпирические потенциалы	Аналитически через конфигурацию давления
Возможность обобщения	Ограничена типами молекул	Масштабируема до биологии, технологий, космологии
Квантовые эффекты	Учитываются через виртуальные фотоны	Не включены в базовую модель, требуют расширения

TTG в текущей формулировке не охватывает квантовые взаимодействия - такие как обмен виртуальными фотонами или флуктуационные корреляции. Однако это не является ограничением, а скорее указанием направления развития: расширение TTG до квантового режима может быть достигнуто через временные операторы, многомерную структуру \rho_t(x,t) и согласование с уравнением непрерывности. TTG не отвергает квантовую картину, а предлагает рассматривать её как моду конфигурации времени, что формирует основу для соединения с микрофизикой.
Таким образом, квантовые эффекты - это не вне TTG, а надстройка, которую теория может включить при переходе от молекулярного масштаба к квантовому.
TTG не отрицает классические модели, а раскрывает их как поверхностные проекции глубинного темпорального поля. Так, притяжение между молекулами становится результатом минимизации геометрии времени, а не энергетического баланса.
7.1.1. Переход TTG к квантовой модели
TTG описывает сцепление как результат конфигурации поля времени \rho_t, v_t, формируя классическую онтологию взаимодействий. Однако при переходе к масштабам, где доминируют квантовые эффекты - суперпозиция, декогеренция, виртуальный обмен - модель требует расширения.
Онтологический переход:
-- В классической TTG взаимодействие - это градиент давления:
-- В квантовом режиме TTG может быть обобщена через операторы плотности времени:
и темпоральные коммутаторы, отражающие нелокальность сцепки и статистическую природу потоков.
Возможный путь - интерпретация квантовой суперпозиции как многомерной структуры v_t между состояниями, где сцепление - это зона минимального P_t в пространстве конфигураций времени. То есть:
Квантовое состояние есть распределение времени, а взаимодействие - топологическое сближение этих распределений.
Декогеренция может трактоваться как потеря темпоральной когерентности, где поле v_t становится разорванным, а \rho_t - флуктуирующим.
Таким образом, TTG может быть расширена до квантовой теории сцепления - не отменяя микрофизику, а предлагая её как выражение геометрии времени.
Это создаёт фундамент для перехода от молекулярных связей к квантовым узлам сцепки, открывая путь к формализации TTG-QFT (темпоральной квантовой теории поля)
7.1.2.Темпоральный принцип неопределённости (TTG-формулировка)
В рамках TTG минимальный масштаб сцепки и темпоральная разрешающая способность связаны со структурой плотности времени \rho_t и градиентом потока \nabla v_t. Предлагаемая эвристическая формула:
\Delta r \cdot \Delta v_t \gtrsim \frac{\hbar}{m}
где:
- \Delta r - пространственная протяжённость зоны сцепления
- \Delta v_t - разброс потока времени
- m - масса частицы
- \hbar - постоянная Планка
Это выражение означает, что точная локализация потока времени требует минимальной геометрической области - иначе сцепка теряет устойчивость. В TTG сцепление - это не обмен, а согласование временной структуры, и любая попытка её "сжать" наталкивается на фундаментальный предел.
7.2. Роль TTG в теории связей, вещества и фундаментальных взаимодействий
На языке TTG вещество - это зона стабилизации временного потока. Молекулярные связи формируются не потому, что электроны "обмениваются" энергией, а потому что структура времени между ними приобретает устойчивую метрику.
TTG-функции:
-- Формирует картину сцепления как конфигурацию поля, а не как результат обмена.
-- Предлагает универсальный язык для описания связи от молекул до макросистем.
-- Превращает межмолекулярную силу в феномен ориентации времени.
-- Строит мост между физикой вещества и космологией, где время - активный агент.
Это даёт возможность согласовать сцепление вещества с расширением Вселенной, предположить, что и галактики удерживаются не только гравитацией, но и глобальной конфигурацией времени - как сцепки во временной ткани.
7.3. Возможности расширения: квантовая механика, биология, технологии
TTG - это онтология, которая может имплантироваться в разные дисциплины:
Квантовая механика:
-- TTG может предложить темпоральное основание суперпозиции, где состояние - это локальное распределение времени.
-- Состояние сцепки может рассматриваться как зона минимума P_t, а не как сумма состояний.
Биология:
-- Взаимодействие белков, ДНК, мембран может быть переосмыслено как синхронизация потока времени.
-- Объяснение специфичной направленности биологических связей через ориентацию v_t.
Технологии:
-- Создание темпоральных клеев - материалов с управляемым потоком времени.
-- TTG-композиты: вещества, где сцепление регулируется через поле v_t(x,t).
-- Наноструктуры с программируемым сцеплением, чувствительным к временной геометрии.
Финальное замечание
TTG не просто описывает сцепление - она делает его проявлением структуры самой реальности. Эта теория открывает путь к синтезу между физикой микросвязей и макровремени, между молекулой и Вселенной, предлагая язык, где сцепка - это не сила, а резонанс метрик времени.
8. Выводы
8.1. Сводка результатов
В данной работе была предложена Теория Темпоральной Гравитации (TTG) как альтернативная интерпретация межмолекулярного сцепления. Показано, что:
-- Потенциал Леннард-Джонса и силы Ван-дер-Ваальса могут быть воспроизведены через градиенты темпорального давления P_t = \kappa \rho_t v_t^2.
-- TTG-сила F_t = -\nabla P_t аналитически и численно совпадает с классическим профилем взаимодействия.
-- Введено понятие временной сцепки как структуры потока времени между молекулами.
-- Разработаны экспериментальные схемы, включая концепт временной камеры, способной выявить TTG-эффекты.
-- TTG интегрируется с классическими подходами, расширяя онтологию сцепления до геометрии времени.
Таким образом, сцепление вещества рассматривается как результат локальной стабилизации темпорального поля - феномен, имеющий ясную математическую форму и экспериментальные перспективы.
8.2. TTG как физически проверяемая альтернатива
TTG обладает рядом характеристик, делающих её пригодной для эмпирической проверки:
-- Воспроизводимость формы сцепки в численных графиках и расчётах.
-- Предсказания спектроскопических эффектов при нарушении потока времени.
-- Возможность управляемых экспериментов с TTG-полем в нано- и макроструктурах.
-- Отличие от флуктуационных и электродинамических моделей, позволяющее выявить TTG-сигнатуры.
Это делает TTG не просто философской концепцией, а рабочей физической теорией, пригодной для верификации.
8.3. Перспективы развития темпоральной физики вещества
TTG открывает широкие направления для дальнейших исследований:
-- Углубление математической структуры \rho_t, v_t: анализ симметрий, интегралов, топологии временного поля.
-- Согласование с квантовой механикой: трактовка суперпозиции как распределения времени, переход к темпоральным операторам.
-- Применение в биофизике: сцепление белковых доменов, ДНК и мембран через темпоральную метрику.
-- Создание TTG-материалов: веществ с регулируемой сцепкой по геометрии потока времени.
-- Интеграция с космологией: сцепление масштабных структур Вселенной как проявление глобальной конфигурации времени.
Таким образом, TTG закладывает фундамент темпоральной физики вещества, где сцепление - не частный эффект, а выражение структурной динамики времени.
9. Заключение: TTG как язык реальности
TTG демонстрирует, что сцепление между нейтральными молекулами - включая силы Ван-дер-Ваальса - может быть получено из конфигурации темпорального поля, без обращения к флуктуационной динамике. Теория вводит физический механизм взаимодействия через градиент давления времени -\nabla P_t, воспроизводя форму потенциальной ямы Леннард-Джонса и предлагая трактовку притяжения как структурную стабилизацию потока времени.
Ключевые элементы модели - плотность времени \rho_t, поток v_t, давление P_t = \kappa \rho_t v_t^2 - составляют геометрическую онтологию сцепки, применимую к описанию молекулярных, биологических и даже космологических структур. TTG не отвергает классические подходы, но раскрывает их как проявления конфигурации времени, объединяя энергетическую и структурную картины взаимодействия.
Таким образом, TTG - это не просто теория сцепления. Она - язык, в котором взаимодействие, стабильность и форма материи описываются через геометрию времени. Сцепка становится выражением конфигурационной согласованности потока, а реальность - тканью, структурированной во временной метрике.
TTG завершает путь от эмпирических моделей к онтологически обоснованной физике сцепления - платформе, способной соединить молекулярное и фундаментальное в едином формализме времени.
10. Литература

On the Determination of Molecular Fields

106

Intermolecular and Surfa

ce Forces

The End of Time: The Next Revolution in Physics

The Order of Time

Time, Reality an

d Experience

The Road to Reality: A Complete Guide to the Laws of the Universe

Wholeness and the Implicate Order

A Brief History of Time

Cosmological and Black Hole Apparent Horizons

Quantum Gravity from Causal Dynamical Triangulations: A Review

Class. Quantum Grav.

DOI: 10.1088/1361-6382/ab57c7

Quantifying diel

ectric permittivities in the nonlinear regime

J. Phys.: Condens. Matter

DOI: 10.1088/1361-648X/ac108f

Complete coherence of random, nonstationary electromagnetic fields

Opt. Lett.

DOI: 10.1364/OL.420573

11.Appendix A: Потенциальные области применения TTG
Модель темпоральной сцепки (TTG), как описано в основном тексте, основывается на конфигурации темпорального давления P_t = \kappa \rho_t v_t^2 и его пространственно-временном градиенте \nabla P_t. В различных дисциплинах проявляются аналогичные механизмы: от устойчивости связей в биомолекулах до макроскопических структур материалов. Ниже представлены области, в которых формализм TTG может быть применён или адаптирован, основанные на прямых аналогиях с физическим содержанием модели.
A.1. Биомолекулярные взаимодействия
Формализм TTG применим к анализу внутримолекулярной сцепки, включая:
-- Стабильность водородных и гидрофобных связей
-- Комплексообразование между белками и лигандами
-- Упаковку и развёртывание ДНК
Это позволяет интерпретировать взаимодействия как минимизацию темпорального давления P_t в сцепленных зонах.
Таблица A1. Биологические структуры и сцепка TTG

Явление	TTG-интерпретация	Методологическая поддержка
Белково-белковая сцепка	\nabla P_t задаёт устойчивость комплекса	ИК-спектроскопия, MD-моделирование
ДНК-суперспирализация	Поток v_t управляет упаковкой	Электрофоретика, AFM
Лигандное связывание	Локальная сцепка \phi(\rho_t, v_t)	Кинетика связывания, спектроскопия

A.2. Наноструктуры и материалы
Сцепка в TTG может быть адаптирована для моделирования:
-- Анизотропии сцепки в метаматериалах
-- Устойчивости фаз в сверхтвёрдых веществах
-- Самосборки наномолекул через конфигурации v_t
Таблица A2. TTG-моделирование в материаловедении

Система	TTG-подход к сцепке	Потенциальные применения
Метаматериалы	Конфигурация потока v_t управляет связями	Оптимизация направленных свойств
Самоорганизующиеся структуры	Минимизация \nabla P_t формирует сборку	Наносборка, дизайн композитов
Фазовые переходы	Нарушение темпоральной симметрии	Теория сцепочной стабилизации

A.3. Космологические интерпретации
Ограниченно, TTG допускает теоретическую интерпретацию:
-- Расширения Вселенной как темпорального градиента \nabla v_t
-- Геометрии крупномасштабных структур через распределение \rho_t(x)
-- Фазовых переходов в ранней Вселенной как локальных нарушений P_t
Таблица A3. Космологические структуры и TTG-аналогии

Явление	TTG-интерпретация	Уровень обоснования
Расширение Вселенной	Градиент v_t как динамический масштаб	Гипотетическое направление
Структура галактик	Конфигурации \rho_t(x)	Математическая аналогия
Космическое фоновое поле	Слабые сцепки во временной метрике	Теоретическая спекуляция

Формулировки об "узлах" или "сцепке галактик" исключены.
A.4. Формализм в теории поля и математической физике
TTG предлагает:
-- Построение лагранжианов темпорального поля
-- Формализацию коммутаторов [\hat{r}, \hat{v}_t] = i \hbar/m
-- Топологическую классификацию узлов сцепки
Таблица A4. Теоретические структуры TTG в физике

Концепт	TTG-аналог	Возможности обобщения
Лагранжиан поля времени	\mathcal{L} = \frac{1}{2}(\partial_\mu v_t)^2 - V(\rho_t)	Альтернатива полям взаимодействий
Калибровочная симметрия	Группа T(1): v_t \mapsto v_t + \alpha	Модель сцепочной инвариантности
Топологические состояния	Узлы давления P_t	Классификация фазы сцепки

Оставить комментарий © Copyright Лемешко Андрей Викторович (biomarket@ukr.net) Размещен: 17/07/2025, изменен: 05/10/2025. 57k. Статистика. Статья: Естествознание Физика времени Иллюстрации/приложения: 4 шт. Скачать:		Ваша оценка:
Аннотация: Теория темпоральной гравитации и природа сил Ван-дер-Ваальса

Лемешко Андрей Викторович Время как основа сил Ван-дер-Ваальса

Лемешко Андрей Викторович
Время как основа сил Ван-дер-Ваальса