Силы притяжения, действующие на тело внутри диска
Путенихин П.В.
http://samlib.ru/img/p/putenihin_p_w/dc15/darc310d.pdf
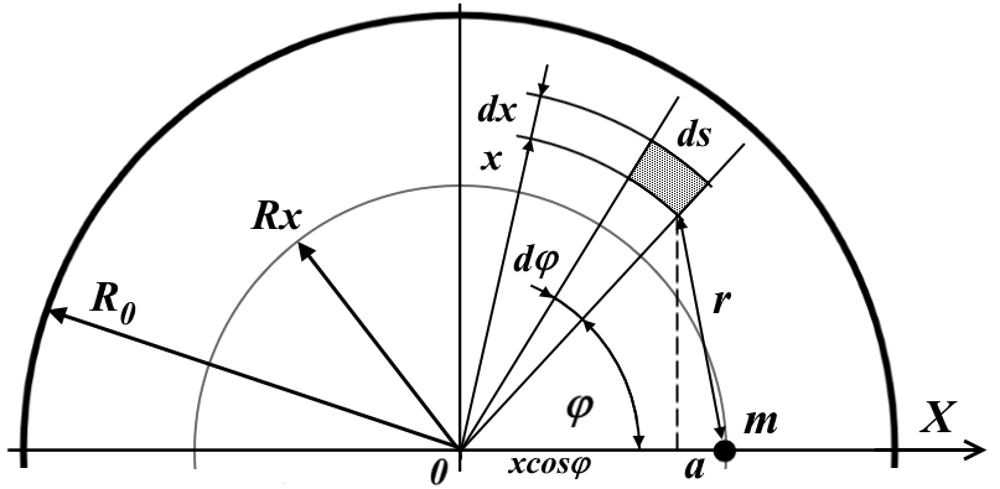
Рис.1.1. Сила притяжения между дифференциалом dM массы диска и пробным телом m внутри диска
![]()
![]() (1.1)
(1.1)
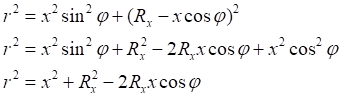 (1.2)
(1.2)
![]()
![]()
![]()
![]()
![]()
![]()
(1.3)
![]() (1.4)
(1.4)
![]() (1.5)
(1.5)
![]()
![]() (1.6)
(1.6)
![]() (1.7)
(1.7)
![]()
![]()
![]()
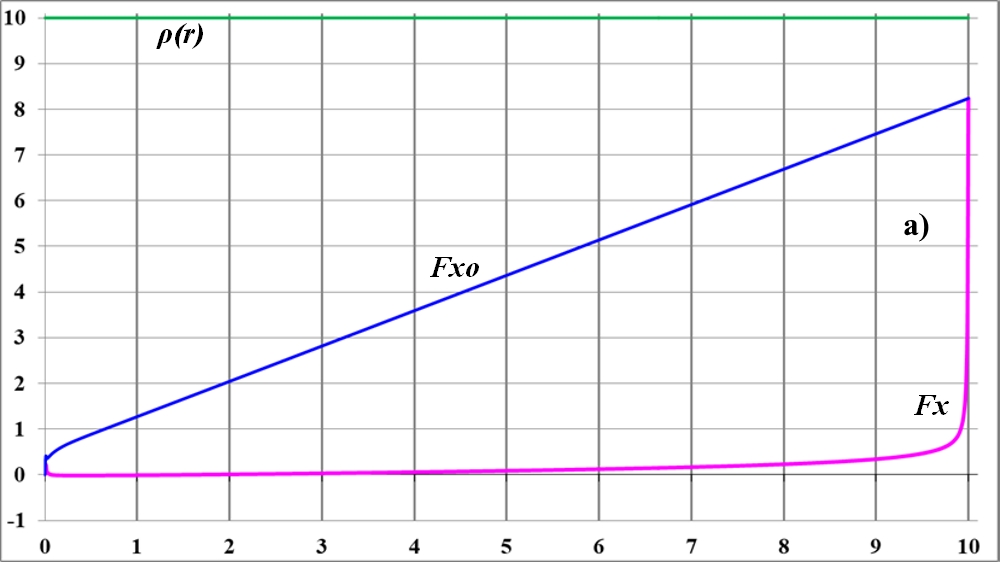
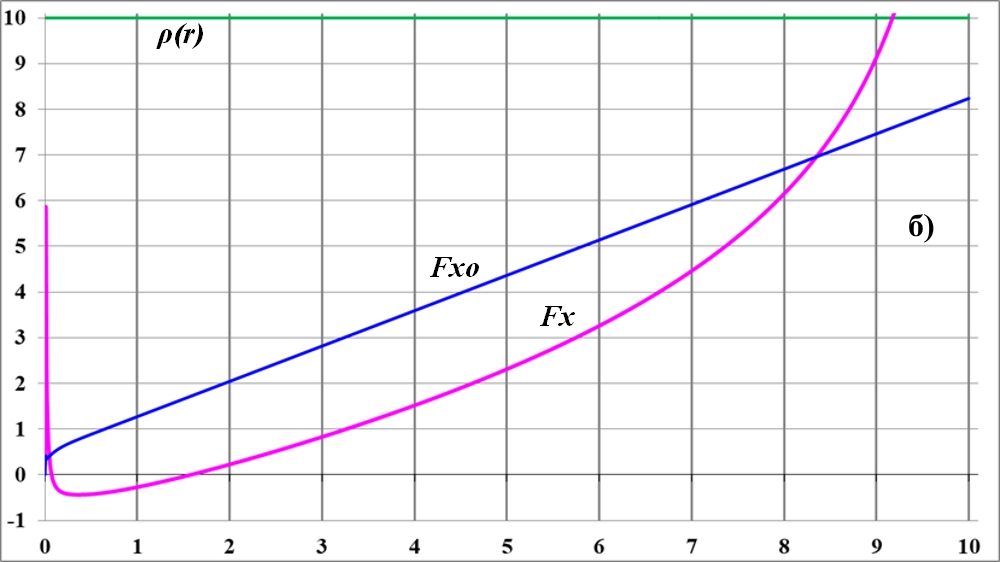
Рис.2.1. Силы притяжения Fxo - только от внутренних обручей; Fx - от всех обручей; a) - равные масштабы; б) - график Fx в увеличенном масштабе
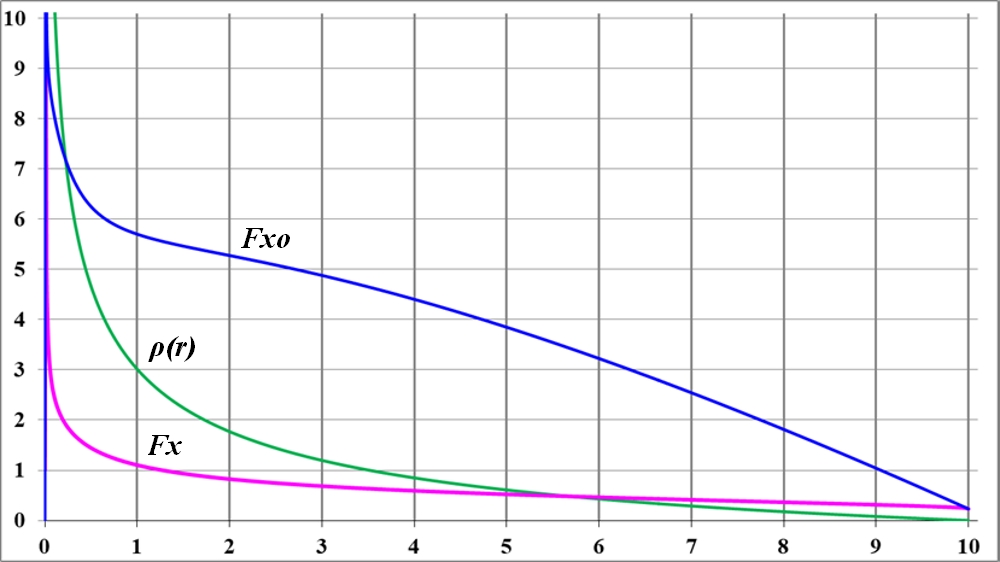
Рис.2.2. Силы притяжения диска с гиперболической функцией плотности: Fxo - только от внутренних обручей; Fx - от всех обручей
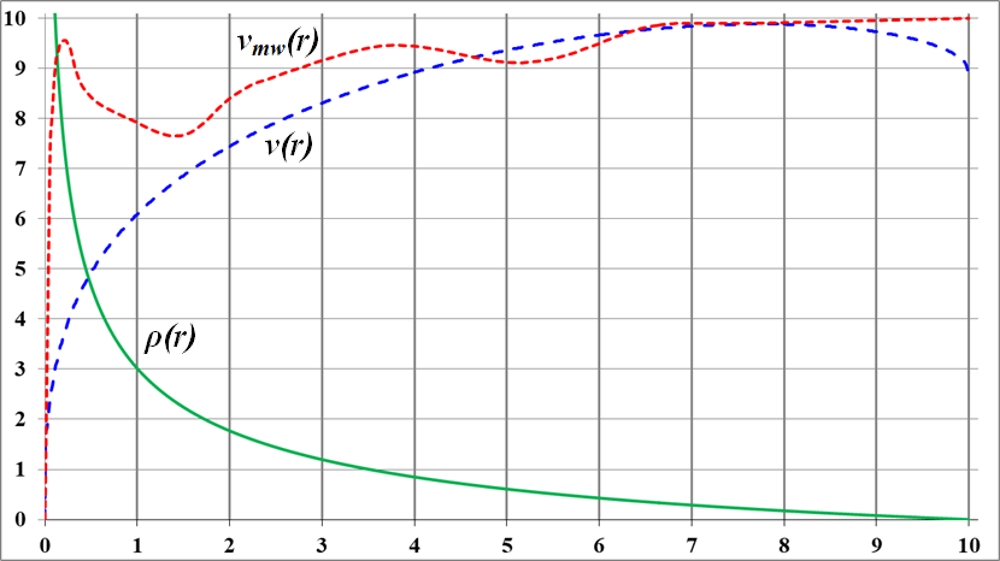
Рис.2.3. Диск с гиперболической функцией плотности имеет кривую вращения, приближающуюся к наблюдаемой кривой вращения галактики Млечный Путь
![]() (2.1)
(2.1)
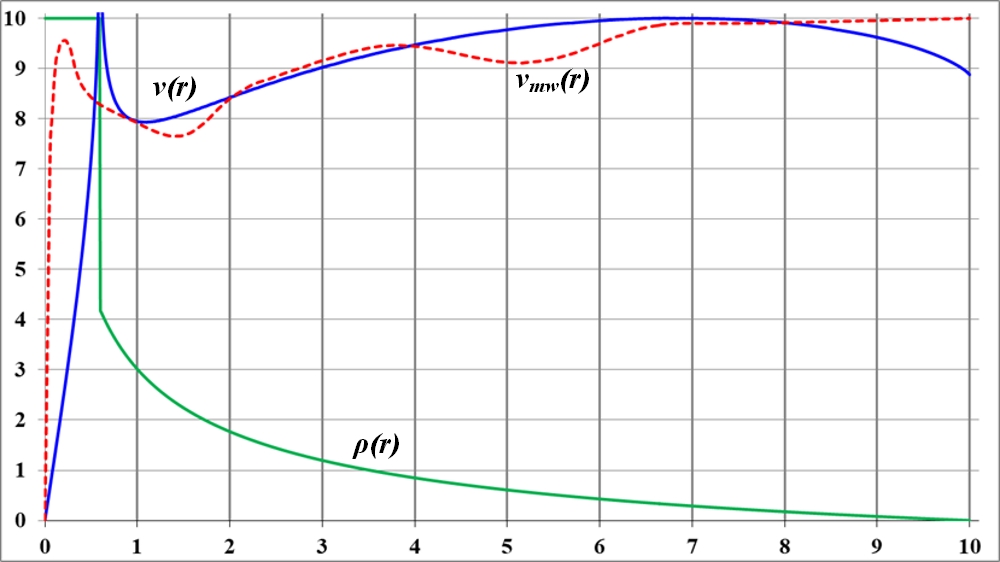
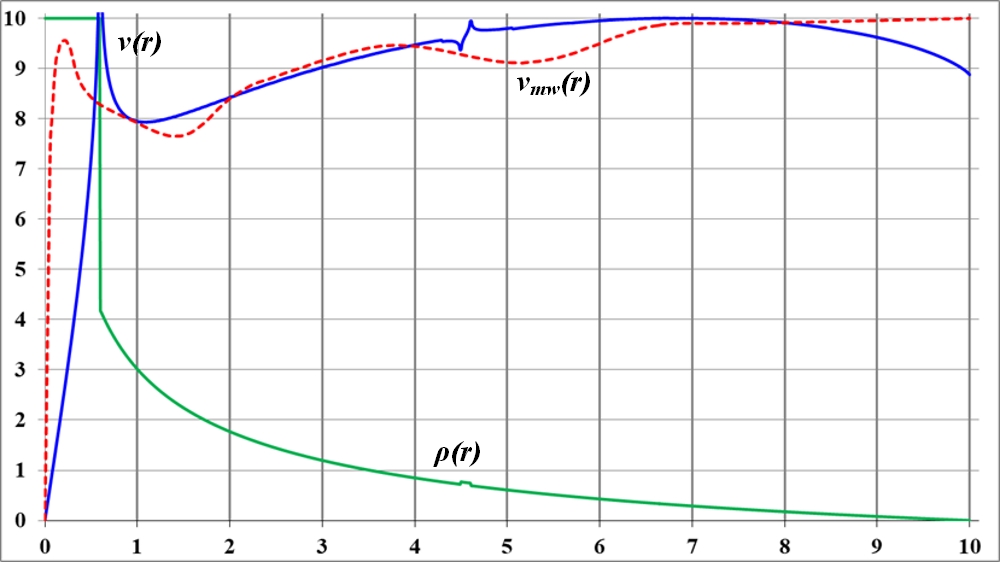
Рис.2.5. Небольшой выступ на графике плотности ведёт к сильному искажению, всплеску на кривой вращения
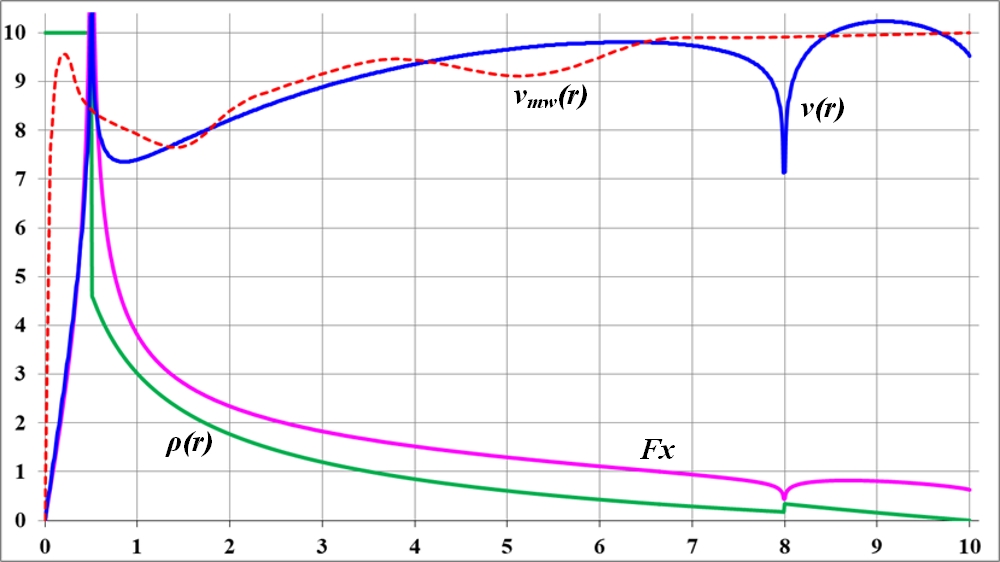
Рис.2.6. Ступенька на графике плотности ведёт к сильному искажению, пику на кривой вращения
![]()
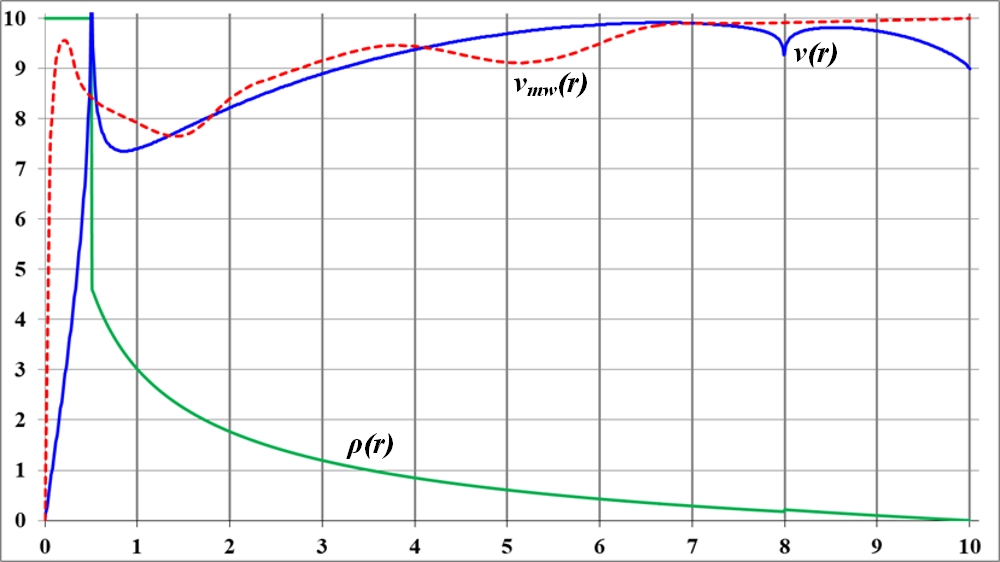
Рис.2.7. Пик на кривой вращения возникает при любой, даже самой малой ступеньке на графике плотности
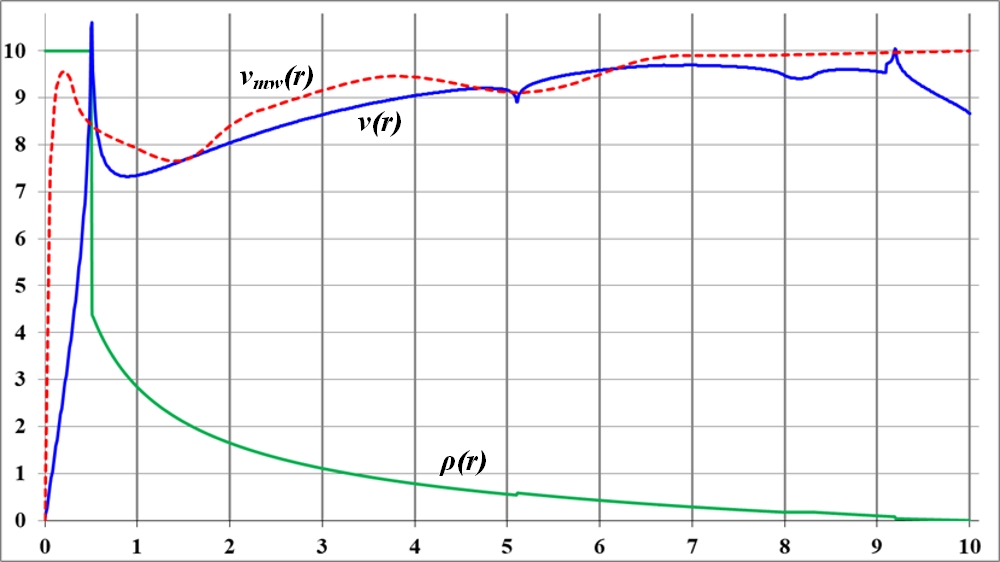
Рис.2.8. Плавный изгиб, переход на графике плотности ведёт к такому же плавному изгибу на кривой вращения
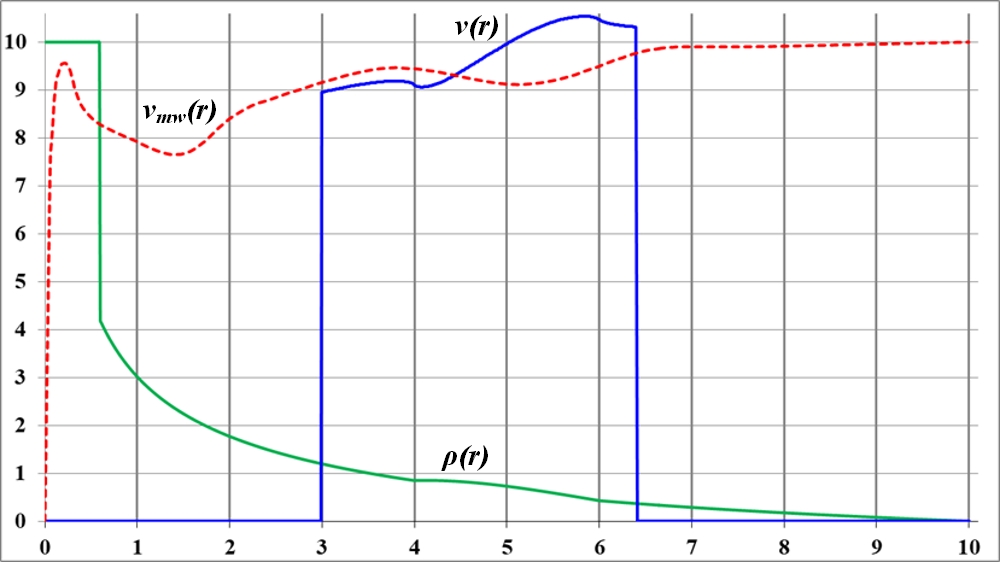
Рис.2.9. Плавный параболический изгиб на графике плотности привёл к значительному, но плавному изгибу на кривой вращения
![]()
![]()
![]()
![]()
![]()
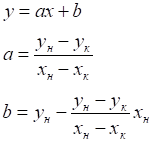
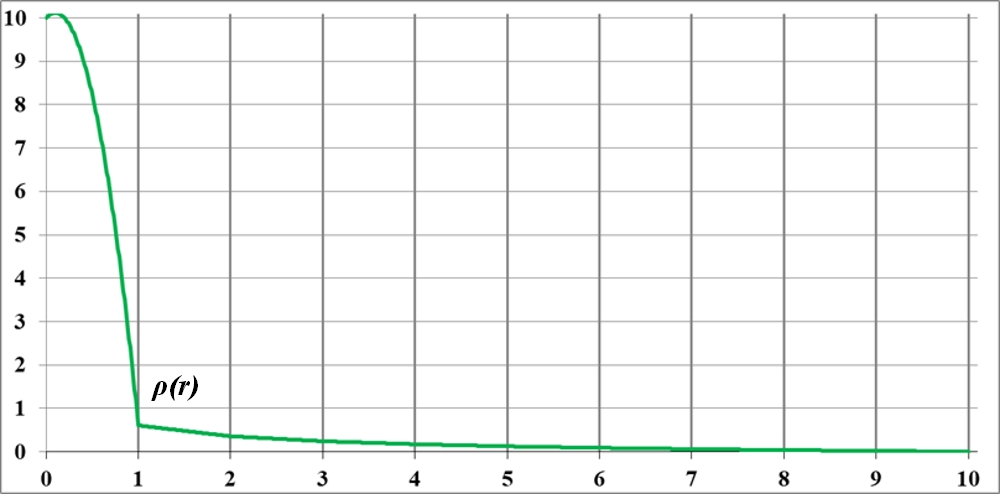
Рис.3.1. Исходная функция плотности
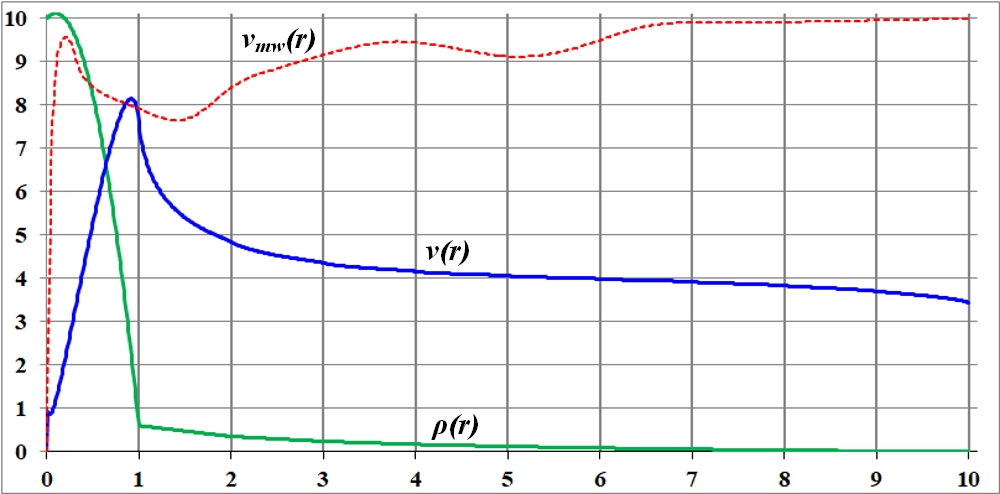
Рис.3.2. Кривая вращения по исходной функции плотности
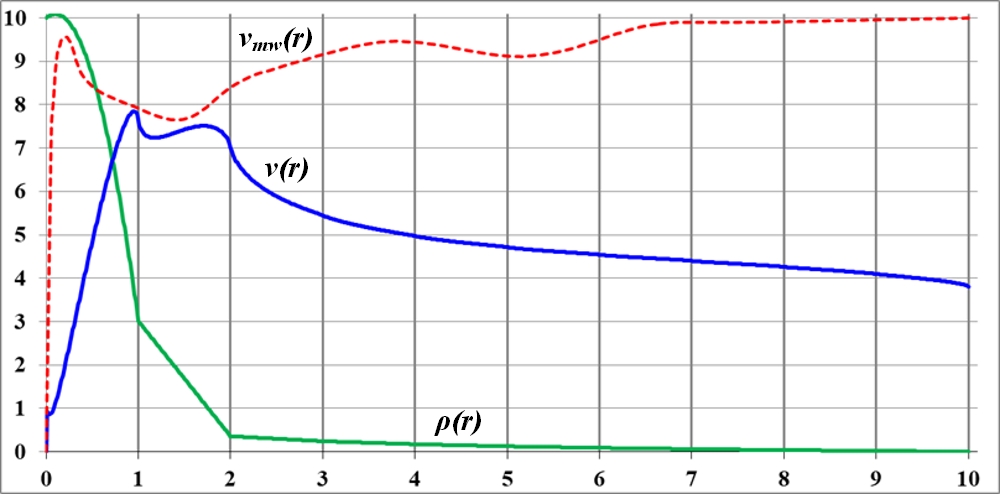
Рис.3.3. Кривая вращения после деформации исходной функции плотности
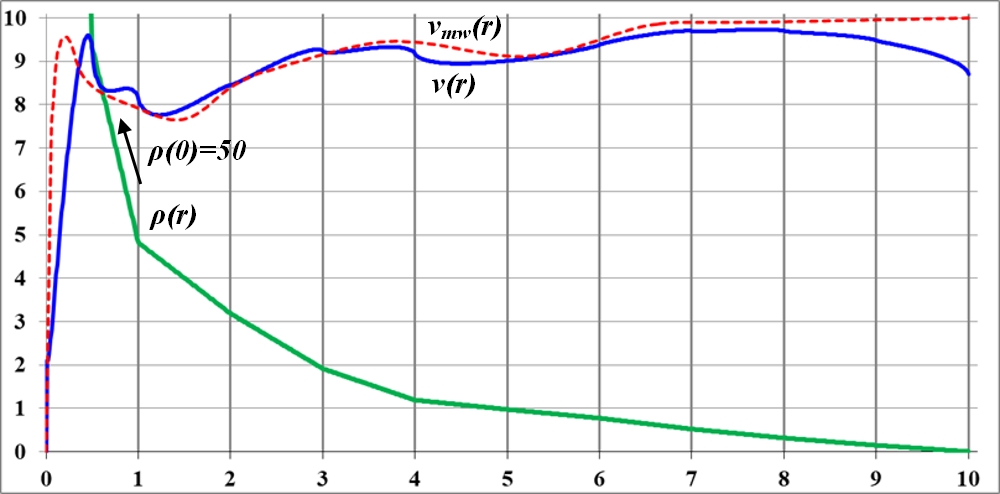
Рис.3.4. Первое приближение кривой вращения к эталону
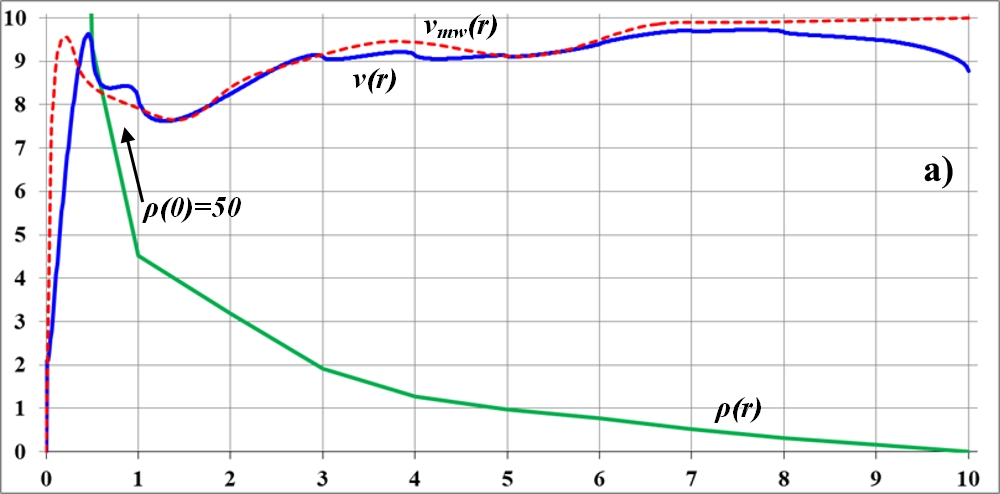
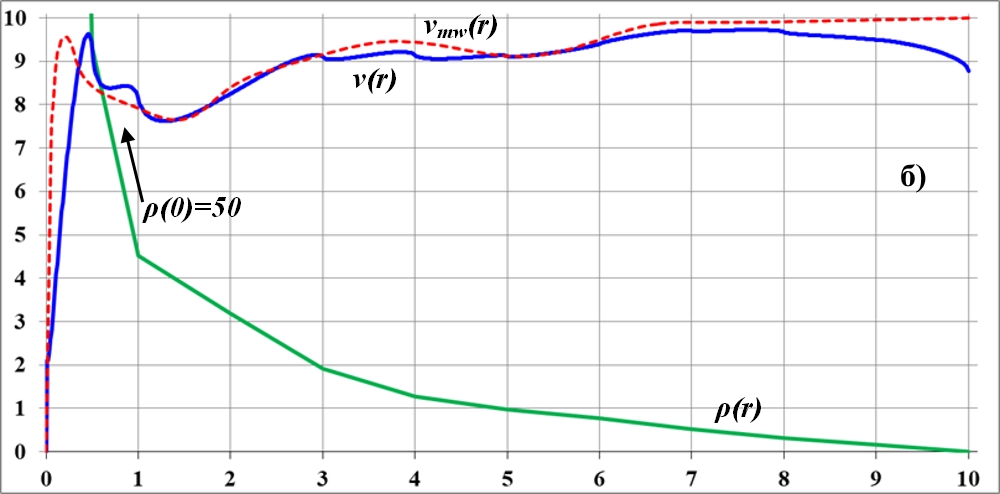
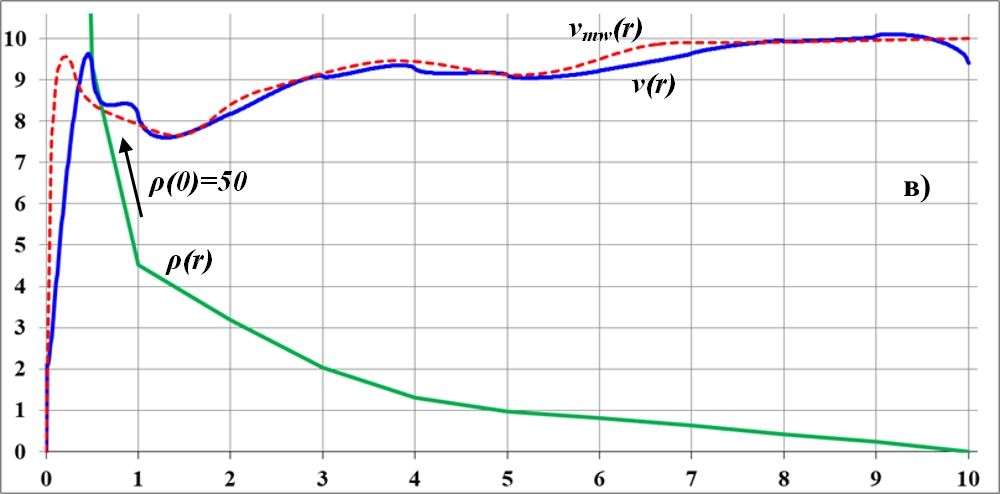
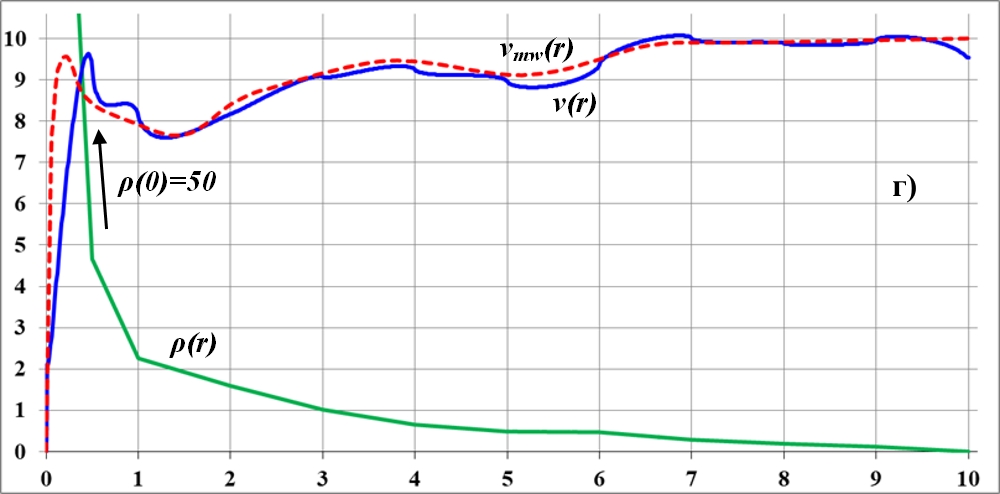
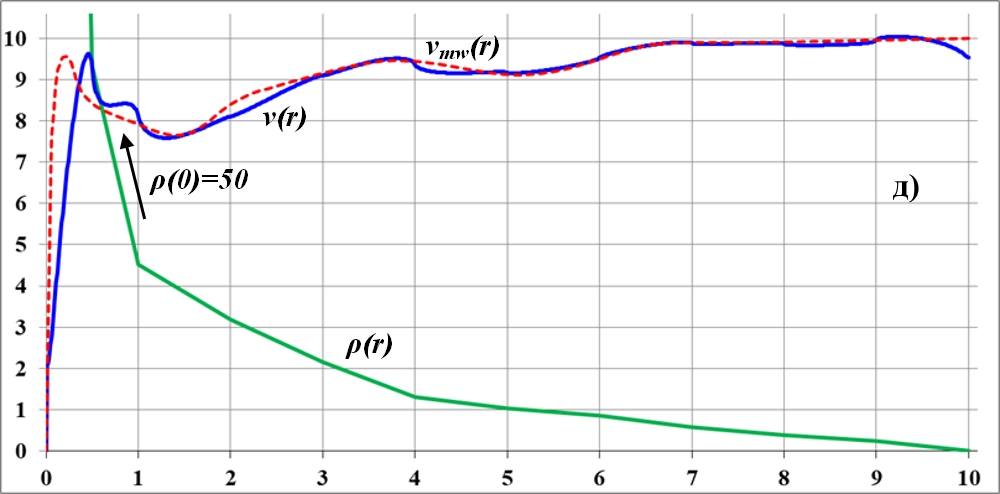
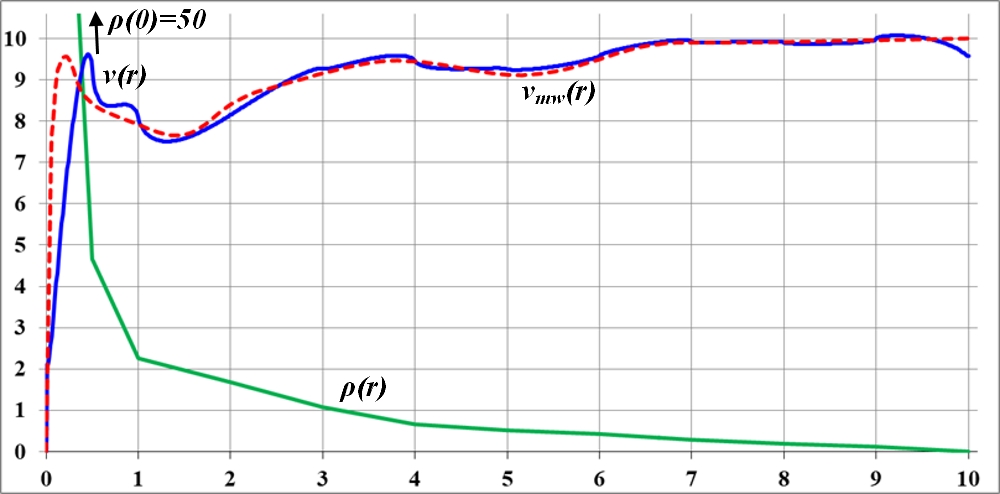
Рис.3.5. a)...д) - последовательные приближения кривой вращения v(r) диска к эталону - кривой вращения vmw(r) галактики Млечный Путь
![]() (4.1)
(4.1)
![]()
![]() (4.2)
(4.2)
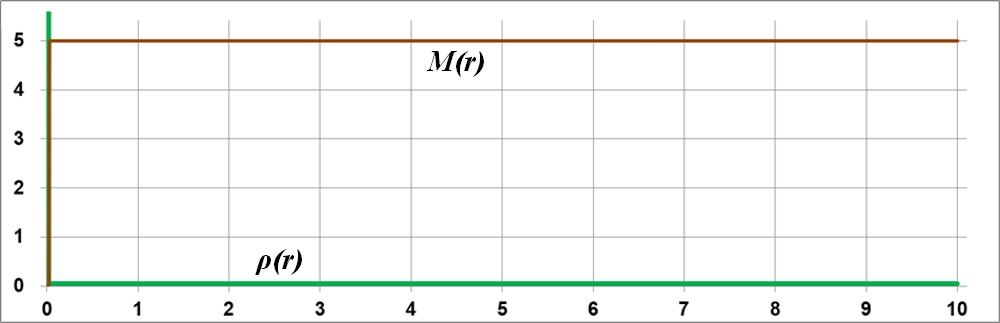
Рис.4.1. При нахождении всей массы в центре диска массы M(r) всех частичных, вложенных дисков равны этой массе
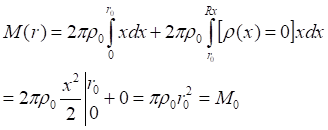
![]()
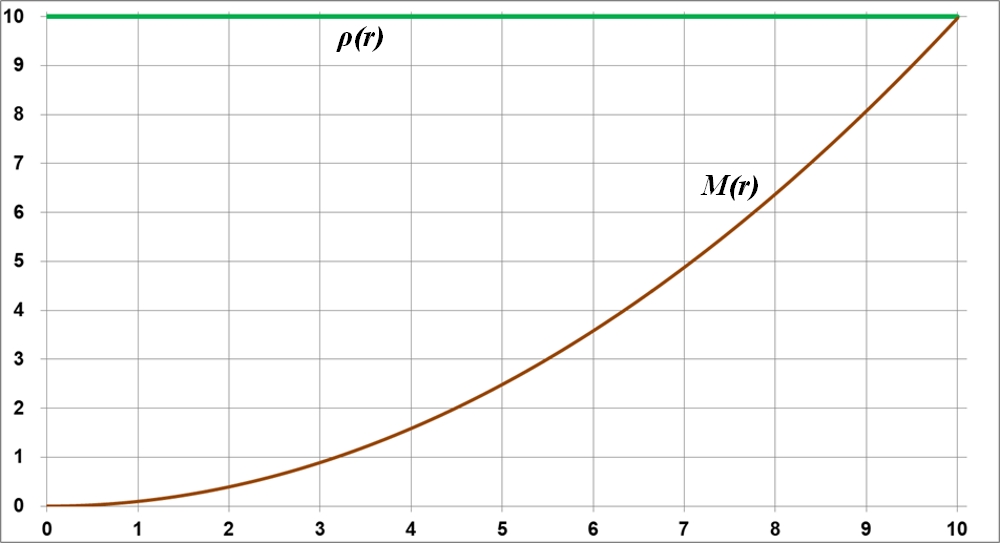
Рис.4.2. В однородном диске массы всех частичных, вложенных дисков растут пропорционально квадратам их радиусов
![]()
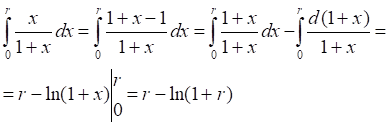
![]()
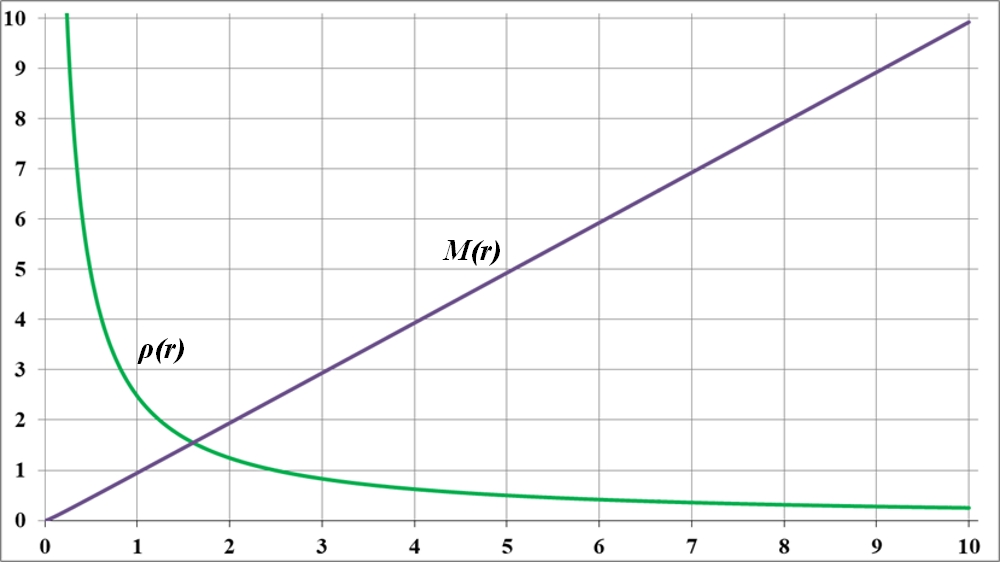
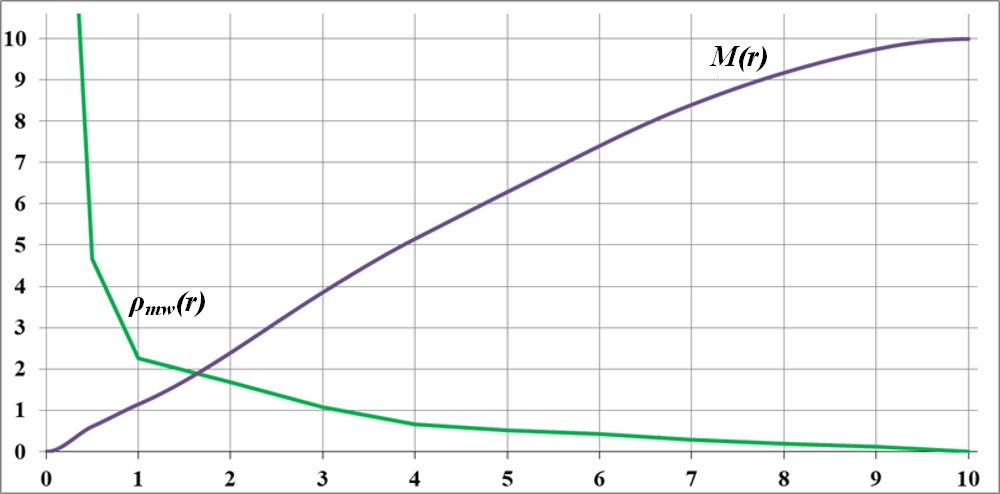
Рис.4.4. Распределение массы диска с функцией плотности ρ(r), подобранной под наблюдаемую кривую вращения vmw(r) галактики Млечный путь
12.12.2020 - 26.02.2021